一、CORDIC算法
CORDIC(Coordinate Rotation DIgital Computer)是一种通过迭代实现快速平面旋转的算法,通过变形扩展,它可以对多种超越函数求值,例如三角/反三角函数、双曲函数等。
对超越函数求值,常见方法为用多项式近似,例如利用泰勒展开来逼近目标函数,只要阶数取得足够大,就可以无限逼近目标函数。当我们把这个方法运用到某些特殊机器时,很快会发现问题:泰勒展开包括大量复杂浮点运算,对于没有硬件浮点运算单元的机器,只能通过软件浮点实现。
CORDIC的出现解决了这个问题。该算法利用迭代逼近的方法,仅仅通过加/减和移位操作即可计算,极大的方便了机器实现。
本文的:
一、解释CORDIC旋转的原理。
二、从旋转模式出发,解释三角函数(sin, cos, tan)的计算;
三、从旋转模式出发,解释反三角函数(arcsin、arccos)的计算;
四、从向量模式出发,解释向量模的计算;
五、介绍定点运算的实现及软件模型的建立
六、通过Verilog HDL设计硬件。
本文代码仓库详见:https://github.com/cassuto/CORDIC-all-in-one-verilog
二、核心思想
正如该算法的名字所说,CORDIC最初是为一种用来进行坐标轴旋转的专用计算机开发的(其原型硬件于1959年成功应用于实时导航)。追根溯源,CORDIC的核心就是坐标轴旋转。其后又由不同的旋转方式导出了各类超越函数的计算方法。
CORDIC包括旋转模式和向量模式,下面逐一解释。
1、旋转模式
1.1 伪旋转
假设现要将一个直角坐标系中的点P(x0, y0)绕原点逆时针旋转z0角度,则变换后的点P1(x1, y1)坐标如下:
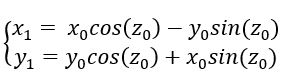
我们发现这个转换式中涉及三角函数,但现在假设机器还不能求任意三角函数值,那么能否改进?
继续观察旋转变换式,可以等价得到:
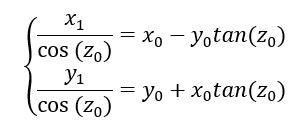
上式仍然涉及两个三角函数,但是cos被放到了一边,于是重点研究tan(z0)。将角度z0微分为n个小角度,每一步旋转θn,通过若干步的旋转最终逼近目标。如果像下面这样特殊选取θn,使tan θn恰好只与2的幂有关,则原本复杂的乘tan θn运算就可以通过二进制右移n位实现(xn,yn都是整数,相关问题在后面讨论),这对二进制计算机非常自然。
$$ tan heta_n = frac{1}{2^n} $$
结合上面的变换公式,令cos θn=Pn,得到如下迭代格式:
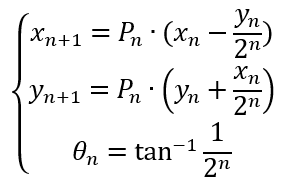
分析计算量。θn = atan(1/2n)可查表得出。同理系数Pn也可以通过查表求出,但它们仍是浮点数。
到这里,算法原先的4次浮点运算,被成功减少到了2次,我们离CORDIC伪旋转算法已经很近了。
但问题还没有结束,如果迭代n次的话,仍需要进行2n次浮点运算。引起2n次浮点运算的原因是每次都需要与系数Pn相乘,这样做真的有必要吗?
构造辅助三角形,可以得出:
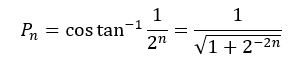
因此Pn的取值只与n有关。完全可以在所有迭代都完成后,再在最终结果上乘P=ΠPn。
对于根据迭代较少的情况,可以将Pn的不同取值固化到表格中,通过查表求出。
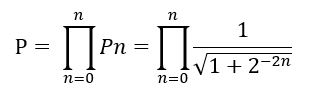
但这仍需查表。进一步分析发现,对于迭代次数较多的情况,可以将Pn看作常数近似处理,因为随着n的增加,Pn逐渐稳定下来:
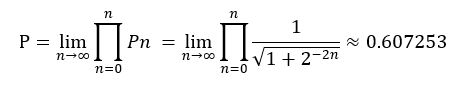
即迭代多次时,可取Pn ≈ lim(n→∞)Pn,这成功去除了Pn查找表。不过引入了截断误差。误差分析至关重要,本文有待完善。
通过数值方法,可以形象地看出Pn随n增大的变化趋势。
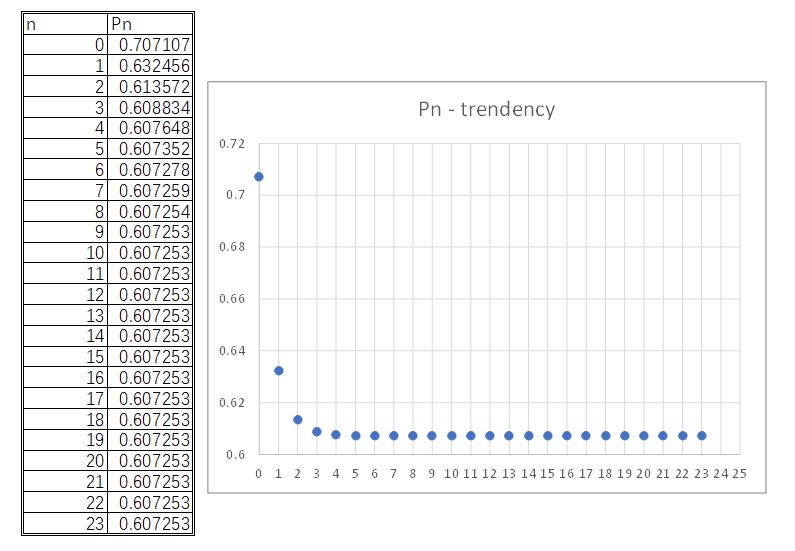
同理可得顺时针方向的旋转算法。
对两旋转方向的公式进行归纳:定义符号函数S(n)控制旋转方向,逆时针旋转时S(n)取1;顺时针旋转时S(n)取-1。可以写出更一般的伪旋转公式:
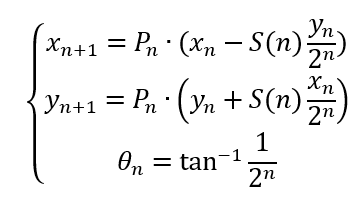
(式1.1-1)
至此我们得到了一个完整的旋转算法,一些文献中也称这个过程为“伪旋转”。
1.2 迭代逼近
伪旋转算法虽然避免了复杂的计算,但结果并不一定精确,原因在于每次旋转的角度θn是严格受限的。例如目标角度Z0取30°,第一次旋转θ0=atan(1)=45°,显然已经远远超过了目标角,因此伪旋转算法不一定收敛于精确值。
为了确保结果收敛于精确值,需要引入迭代逼近。思路很直观:上例中“超过了目标角”,就以更小的角度向相反方向旋转;若未“超过”,则继续同向旋转,如此反复,经过无穷次迭代后,点(Xn,Yn)将最终收敛于目标点。
为了实现迭代逼近,首先引入角度累加器Zn,以确定相对于目标角度旋转了多少。Z0取目标角度,规定每步迭代满足:
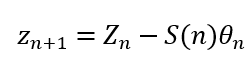
(式1.2-2)
则Zn正是目标角度与累计旋转角度的差值,称为相位误差。如果已经转过的角度大于目标角,则Zn<0,反之Zn>=0。
回到逼近的原理:如果转过的角度大于目标角,则向相反方向旋转,反之则继续同向旋转。发现,这正是Zn+1和S(n)的关系。
假设目标角Z0>0表示逆时针旋转,则S(n)与Zn+1可总结如下:
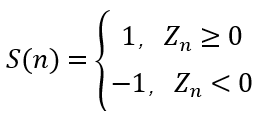
(式1.2-3)
联立式1.1-1、1.2-2、1.2-3,便可得到完整的旋转算法。可以证明,当n→∞时,Zn→0,点(Xn, Yn)将收敛于目标点。
称这种CORDIC模式为旋转模式。
上述算法可用伪代码描述如下:
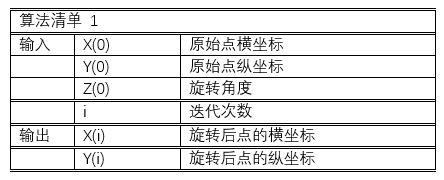
1 For n=0 to i-1 2 If (Z(n) >= 0) Then 3 X(n + 1) := X(n) – (Yn >> n) 4 Y(n + 1) := Y(n) + (Xn >> n) 5 6 Z(n + 1) := Z(n) - atan(1/2^n) 7 Else 8 X(n + 1) := X(n) + (Yn >> n) 9 Y(n + 1) := Y(n) – (Xn >> n) 10 11 Z(n + 1) := Z(n) + atan(1/2^n) 12 End if 13 End for
14 X(i) *= 0.607253 // limP
15 Y(i) *= 0.607253 // limP
1.3 通过旋转模式计算三角函数
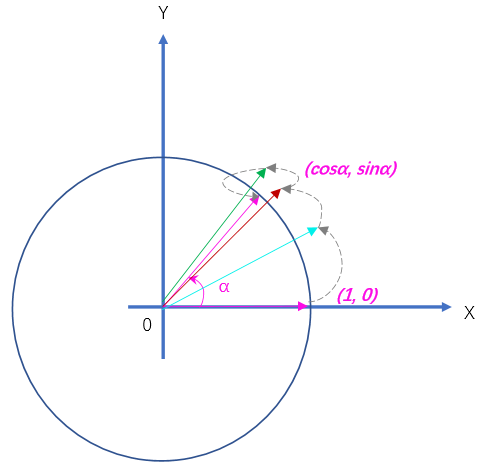
借助单位圆工具,在直角坐标系中,将点(1, 0)以原点为中心逆时针旋转α角,旋转后点的坐标(x',y')正是(cosα, sinα)。
下图显示了CORDIC算法计算三角函数的迭代过程。
2、向量模式
向量模式是为了计算向量模和反三角函数而引出的。
1.1 向量模的计算
直角坐标系中,设目标向量V(x0, y0),向量模的定义如下:
![]()
向量模的计算:将点P0(x0, y0)作为初始坐标。如果将点P0旋转某个角度,使纵坐标y'=0,则此时横坐标x'即为向量V(x0, y0)的模。
与CORDIC旋转模式类似,关键在于逼近的目标不同。取S(n):
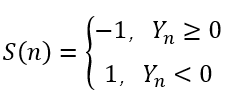
则旋转过程中,Zn→0,向量将向Yn=0的方向逼近,其过程如下(注意图中向量模长比例并不精确):
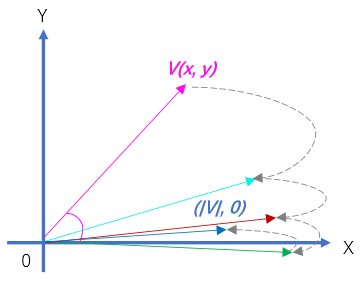
算法用伪代码描述如下:
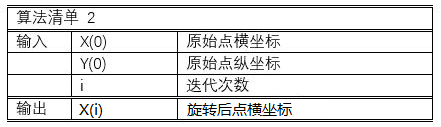
1 limP := 0.607253 2 For n=0 to i-1 3 If (Y(n) >= 0) Then 4 X(n + 1) := X(n) + (Yn >> n) 5 Y(n + 1) := Y(n) - (Xn >> n) 6 Else 7 X(n + 1) := X(n) - (Yn >> n) 8 Y(n + 1) := Y(n) + (Xn >> n) 9 End if 10 End for
11 X(i) *= limP
1.2 反正弦函数的计算
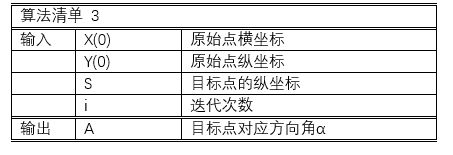
已知正弦函数值S,在直角坐标系中,若当点(1, 0)逆时针旋转某个角度A时纵坐标恰等于S,则A=asinS 即为反正弦函数的值。可见这只是正弦函数计算的逆过程。
仍为向量模式,只是逼近的目标发生了变化。取Zn = Y(n) - S,Zn为纵坐标相对于S的误差。
则旋转过程中,Zn向量将不断向竖直分量Yn=S的方向逼近。
算法用伪代码描述如下:
1 A := 0
2 S /= limP
3 For n=0 to i-1 4 If (Y(n) >= S) Then 5 X(n + 1) := X(n) + (Yn >> n) 6 Y(n + 1) := Y(n) - (Xn >> n) 7 8 A := A + atan(1/2^n) 9 Else 10 X(n + 1) := X(n) - (Yn >> n) 11 Y(n + 1) := Y(n) + (Xn >> n) 12 13 A := A - atan(1/2^n) 14 End if 15 End for
同理可得反余弦函数的计算。
总结,CORDIC旋转模式可完成sinA、cosA、asinA、acosA的计算。
三、定点算法的软件模型建立
定点数
定点数可通过整数来表示。
1、量化角度:在直角范围内,将b位无符号整数的取值区间均分为coeff1 = 2^b / 90 个单位。
则对应任意给定的浮点角度Z°,其对应的整数可表示为:floor(Z * coeff1);
2、转换坐标(x, y):将原始坐标放大coeff2倍并取整即可得出定点坐标。coeff2应根据实际问题适当选取,尽量减小舍入误差。
坐标用整数可表示为:(floor(X * coeff2)、floor(Y * coeff2))。
3、对于算法的整数输出,只需将整数除以相应coeff即可得到对应的浮点数。
浮点数到定点数的转换过程将引入舍入误差。
软件模型
软件的抽象程度高于硬件,可以更加紧凑地对算法进行描述,同时能快速地进行调试。
通过软件实现CORDIC算法:
旋转模式的C语言模型:
https://github.com/cassuto/CORDIC-all-in-one-verilog/blob/master/CORDIC-rotate-fixed-point.c
向量模式的C语言模型:
https://github.com/cassuto/CORDIC-all-in-one-verilog/blob/master/CORDIC-anti-rotate-fixed-point.c
完整软件实现详见:https://github.com/cassuto/CORDIC-all-in-one-verilog
四、FPGA实现
CORDIC在硬件中的典型的应用包括DDS(直接数字频率合成)等等。
本小节主要介绍硬件实现的相关细节,包括象限转换,流水化处理。
象限转换
根据三角函数的对称性,只需实现一个象限,即可得出其余所有象限的情况。
由于相位取值范围被象限四等分,可取相位输入的高2位决定象限。得出象限后,即可根据三角函数值在4个象限的符号关系得到正确的输出。
流水化处理
流水化提高了时钟频率,“以面积换取速度”。
从流水线为空开始,下游模块需等待PIPE_DEPTH+2个时钟周期才能从流水线得出结果;
而当流水线填满后,对于相位输入,流水线都可以在单时钟周期内更新输出。
Verilog设计
输入:相位phase_i。
输出:三角函数值sin_o,cos_o,相位误差err_o
1 module cordic_dds # ( 2 parameter DW = 16, /* Data width */ 3 parameter PIPE_DEPTH = 14, /* Pipeline depth */ 4 parameter limP = 16'h4dba /* P = 0.607253 * 2^15 */ 5 ) 6 (/*AUTOARG*/ 7 // Outputs 8 sin_o, cos_o, err_o, 9 // Inputs 10 clk, phase_i 11 ); 12 13 input clk; 14 input [DW-1:0] phase_i; /* Phase */ 15 output [DW:0] sin_o, cos_o; /* Function value output */ 16 output [DW:0] err_o; /* Phase Error output */ 17 18 reg [DW:0] cos_r=0, sin_o_r=0; 19 reg [DW:0] x[PIPE_DEPTH:0]; 20 reg [DW:0] y[PIPE_DEPTH:0]; 21 reg [DW:0] z[PIPE_DEPTH:0]; 22 23 reg [DW:0] atan_rom[PIPE_DEPTH:0]; 24 25 reg [1:0] quadrant [PIPE_DEPTH:0]; 26 27 integer i; 28 initial begin 29 for(i=0; i<=PIPE_DEPTH; i=i+1) begin 30 x[i] = 0; y[i] = 0; z[i] = 0; 31 quadrant[i] = 2'b0; 32 end 33 end 34 35 initial begin 36 atan_rom[0] <= 8189; 37 atan_rom[1] <= 4834; 38 atan_rom[2] <= 2554; 39 atan_rom[3] <= 1296; 40 atan_rom[4] <= 650; 41 atan_rom[5] <= 325; 42 atan_rom[6] <= 162; 43 atan_rom[7] <= 81; 44 atan_rom[8] <= 40; 45 atan_rom[9] <= 20; 46 atan_rom[10] <= 10; 47 atan_rom[11] <= 5; 48 atan_rom[12] <= 2; 49 atan_rom[13] <= 1; 50 end 51 52 53 // ================= // 54 // Pipeline stages // 55 // ================= // 56 always @ (posedge clk) begin // stage 0 57 x[0] <= {1'b0, limP}; 58 y[0] <= 0; 59 z[0] <= {3'b0, phase_i[DW-1-2:0]}; // control the phase_i to the range[0-Pi/2] 60 end 61 62 always @ (posedge clk) begin // stage 1 63 x[1] <= x[0] - y[0]; 64 y[1] <= x[0] + y[0]; 65 z[1] <= z[0] - atan_rom[0]; // reversal 45deg 66 end 67 68 generate 69 genvar k; 70 for(k=1; k<PIPE_DEPTH; k=k+1) begin 71 always @ (posedge clk) begin 72 if (z[k][DW]) begin /* the diff is negative on clockwise */ 73 x[k+1] <= x[k] + {{k{y[k][DW]}},y[k][DW:k]}; /* >> k */ 74 y[k+1] <= y[k] - {{k{x[k][DW]}},x[k][DW:k]}; /* >> k */ 75 z[k+1] <= z[k] + atan_rom[k]; 76 end else begin 77 x[k+1] <= x[k] - {{k{y[k][DW]}},y[k][DW:k]}; 78 y[k+1] <= y[k] + {{k{x[k][DW]}},x[k][DW:k]}; 79 z[k+1] <= z[k] - atan_rom[k]; 80 end 81 end 82 end 83 endgenerate 84 85 // ================= // 86 // Count quadrant // 87 // ================= // 88 always @ (posedge clk) begin 89 quadrant[0] <= phase_i[DW-1:DW-2]; 90 end 91 generate 92 genvar j; 93 for(j=0; j<PIPE_DEPTH; j=j+1) begin 94 always @ (posedge clk) begin 95 quadrant[j+1] <= quadrant[j]; 96 end 97 end 98 endgenerate 99 100 // ================= // 101 // Adjust quadrant // 102 // ================= // 103 always @ (posedge clk) 104 case(quadrant[PIPE_DEPTH]) 105 2'b00: begin 106 cos_r <= x[PIPE_DEPTH]; /* cos */ 107 sin_o_r <= y[PIPE_DEPTH]; /* sin */ 108 end 109 2'b01: begin 110 cos_r <= ~(y[PIPE_DEPTH]) + 1'b1; /* -sin */ 111 sin_o_r <= x[PIPE_DEPTH]; /* cos */ 112 end 113 2'b10: begin 114 cos_r <= ~(x[PIPE_DEPTH]) + 1'b1; /* -cos */ 115 sin_o_r <= ~(y[PIPE_DEPTH]) + 1'b1; /* -sin */ 116 end 117 2'b11: begin 118 cos_r <= y[PIPE_DEPTH]; /* sin */ 119 sin_o_r <= ~(x[PIPE_DEPTH]) + 1'b1; /* -cos */ 120 end 121 endcase 122 123 assign cos_o = cos_r; 124 assign sin_o = sin_o_r; 125 assign err_o = z[PIPE_DEPTH]; 126 127 endmodule
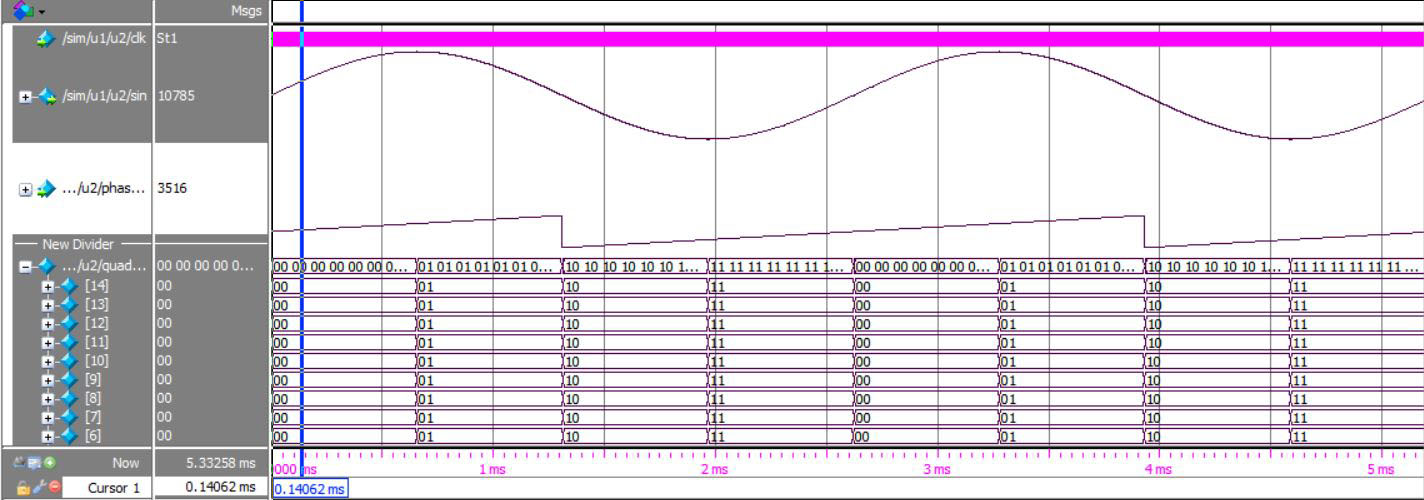
通过仿真得出波形如下: