组合数、杨辉三角与递推算法

一、组合数定义

　　定义从n个不同元素中任意选取m个不同元素构成一组，所有可能取法的个数为组合数，用 $  binom{n}{m} $ 或 $ C_n^m $ 表示。

　　组合数的计算公式可通过排列数导出：

 $$ C_n^m = frac{P_n^m}{m!} = frac{n!}{m!(n-m)!} $$

　　上述公式在计算机中是难解的。因为阶乘的增长速率很大，容易导致中间结果溢出。

 

二、组合数的递推式

　　对于组合数 $ C_n^m $，我们考虑从n个元素中标记一个元素a，并将取法分为如下两类：

　　　　1、取m个元素构成集合A，且a∈A

　　　　　　此时所有可能取法为：

$$ C_{n-1}^{m-1} $$

　　　　　　（首先取出元素a，接下来只需从剩下的n-1个元素中任取m-1个元素）

　　　　2、取m个元素构成集合A，且a ∉ A

　　　　　　此时所有可能取法为：

$$ C_{n-1}^{m}  $$

　　　　　　（因为不包含元素a，需从除a外的n-1个元素中任取m个元素）

　　根据加法原理，便有：

$$ C_n^m = C_{n-1}^{m-1} +  C_{n-1}^{m} $$

　　这便是组合数递推公式的简单推导。

二、杨辉三角与组合数

　　形如下图所示的数字几何排列称为杨辉三角

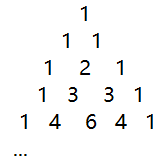
 　　杨辉三角中第n行第m个数C(n, m)满足：

C(n, m) = C(n-1, m-1) + C(n-1, m)（n,m=0,1...，C(n,0)=C(0,m)=1）

　　这就是杨辉三角的递推公式，对比杨辉三角的递推公式与组合数的递推公式

$$ C_n^m = C_{n-1}^{m-1} +  C_{n-1}^{m} （n,m=0,1...）$$ 

我们发现二者完全一致。

　　由此可得出杨辉三角的一个重要性质：杨辉三角的第n行第m个数（n,m=0,1,...）即为组合数 $ C_n^m $

三、组合数的递推计算

　　完全可以通过杨辉三角计算组合数，当然，本质上，这与直接利用递推公式算是一致的。

递推方式计算组合数的C++程序如下。打表时间复杂度为 $ O(N^2) $ ，优点是查询为O(1)，适合有限范围内的多次计算。

#include <bits/stdc++.h>
using namespace std;

const int N=1000;
int c[N][N]; 

void make_comb_table(void)
{
    c[0][0]=c[1][0]=c[1][1] = 1;
    for(int i=2;i<N;++i) {
        for(int j=0;j<=i;++j) {
            c[i][j] = c[i-1][j-1] + c[i-1][j];
        }
    }
}

int main(void)
{
    ios::sync_with_stdio(false);
    make_comb_table();
    int n,m;
    cin>>n>>m;
    cout<<c[n][m];
}