一、序言
关于“深度学习”大部分文章讲的都云里雾里,直到看到“床长”的系列教程以及《深度学习入门:基于Python的理论与实现》,这里主要是对这两个教程进行个人化的总结,目标是让“0基础”的童鞋也能看懂神秘的神经网络。
如果你是AI新手,可以先大概看看《深度学习入门:基于Python的理论与实现》,这本书主要从数学的角度来描述神经网络的各种概念并辅以具体的实现代码。看个大概知道一些概念就行了。然后强烈推荐“床长”的人工智能系列教程(https://www.captainbed.net/),不过我现在也就看到第一章而已。最后推荐大家关注公众号“零基础爱学习”,以后还会继续推送零基础入门的文章。
本文通过使用单个神经元实现图片“手写数字9”的识别,从而引申出神经网络的4个关键函数。大部分代码是前面两个教程内提供的,我做了一些简单的处理。希望看完本文后你会说“哇!好神奇”以及“原来如此!好简单”
二、训练数据获取
要做深度学习,首先面临的第一个问题是,上哪里找到大量的训练数据,好在前辈们已经为我们准备好了一切,就等你来拿了。
MNIST是一个“手写数字”的数据集,包含了6万个训练数据和1万个测试数据,怎么理解呢?就是它提供了7万张图片,图片的内容是手写的各种数字图片,如下图所示(不要在意图片的命名),同时它还提供了图片对应的具体数字称为“标注”。图片+标注的数据对就是我们需要的“大数据”了,所谓AI民工就是干这个“标注”工作的。

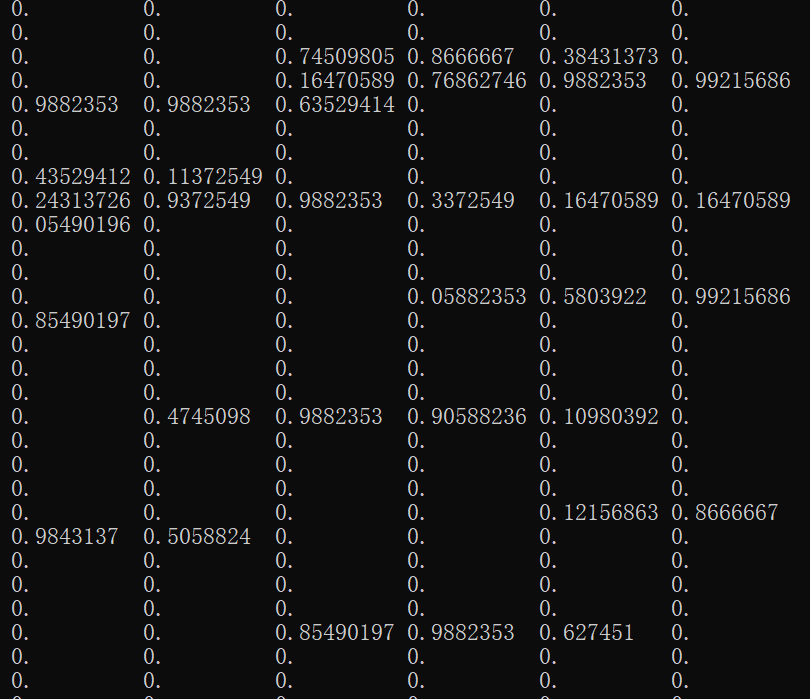
不过MINIST提供的方式不是直接给你下载图片,而是将图片按像素转为像下面这样的一维的数组。数组中0的部分就是图片中黑色的部分,大于零的部分就是图片中白色的部分。

MNIST提供了下载数据集的方法,而在《深度学习入门:基于Python的理论与实现》这本书中附录了”mnist.py“文件,里面已经写好了如何下载mnist数据集并加载到程序中,文末附有下载此文件的方法。
使用此文件时,还需要在你的项目目录中新建一个”datasets”目录。
调用“init_mnist()”函数就自动下载该数据集并以pkl格式保存在本地,以后再次调用会自动检查该文件是否存在,存在的话就不会再次下载了。
调用“load_mnist()”函数可以从pkl文件中导入训练数据和测试数据,每一个数据集包含若干图片和对应的正确标注

如上图,train_img、train_label分别是导入的训练图片和训练标注,test_img、test_label分别是测试用的图片和测试标注。
(所有代码在文末都有的下载方式,不要慌,文章主要讲讲思路)
我们使用print随便输出一个数据看看,print(train_img[9])输出的是一个一维数组,print(train_label[9])输出的是这个一维数组对应的标注。然后你应该注意到这里面的数字都是0.9882353这样的小数,实际上mnist给的是0-255这样的整数,0表示该像素完全黑色,255表示完全白色。每一张图片由28x28个像素组成,每一个数就表示该像素的颜色值(都是黑白图,所以颜色只需要一个维度来表示)。本来应该是28x28的二维数组,为了方便使用就直接转成了1x784的一维数组。我”mnist.py“文件中在导入MNIST数据时将所有数字都除以255,首先所有数据都除以255不影响数据的使用,其次后面一些公式需要像0~1这样的小数才可以正确执行。(后面再讲)

为了简化整个程序,我们只针对数字9做识别,需要对train_label和test_label做一些修改。这样图片内如果写的是9那相应的标注为1,否则为0。
train_label = np.where(train_label==9,1,0) #将标注为9的改为标注1,其他为0
test_label = np.where(test_label==9,1,0)
print(train_label)

至此,我们的数据都准备好了,测试的时候6万个数据似乎有点太多了,所以我们可以裁剪一下,只用6000个数据来训练,1000个数据来测试。
train_img = np.resize(train_img,(6000,train_img.shape[1])) #裁剪数据集
train_label = np.resize(train_label,(6000,1))
test_img = np.resize(test_img,(1000,test_img.shape[1]))
test_label = np.resize(test_label,(1000,1))
裁剪后的数据形状:

但是这样的数据还是没法使用,我们还需要再将数据做一次转置才行(具体原因后面再说)。
train_img = train_img.T
train_label = train_label.T
test_img = test_img.T
test_label = test_label.T
转置后的数据形状:

好了,终于准备好数据了,下面开始深度学习吧。
三、神经网络的4个函数
神经网络最基本的模型其实就是由4个函数组成的,所以你可以看到很多教程只需要十几行代码就可以构建一个深度学习网络,这是真实可行的。它们分别是:
传播函数、激活函数、反向传播函数、损失函数
他们分别实现了几个核心功能:向前预测、输出映射、反向优化、损失计算
乍看上去有点摸不着头脑,我们先来看一下单个神经元的构成示意图:

神经元中x是输入信号、w和b是预测参数、a是预测的基本结果、h()是激活函数、y是最终预测结果以及下一层神经元的输入。对于本文要实现的目标“手写数字9识别”,在训练阶段我们从x输入大量的数据,然后根据y的结果来反向推导w和b的值如何进行优化。在图片识别阶段,使用优化好的w和b值进行一次计算得到y,根据y的值来判断被识别图片是否是数字“9”。下面分别是训练和测试的示意:
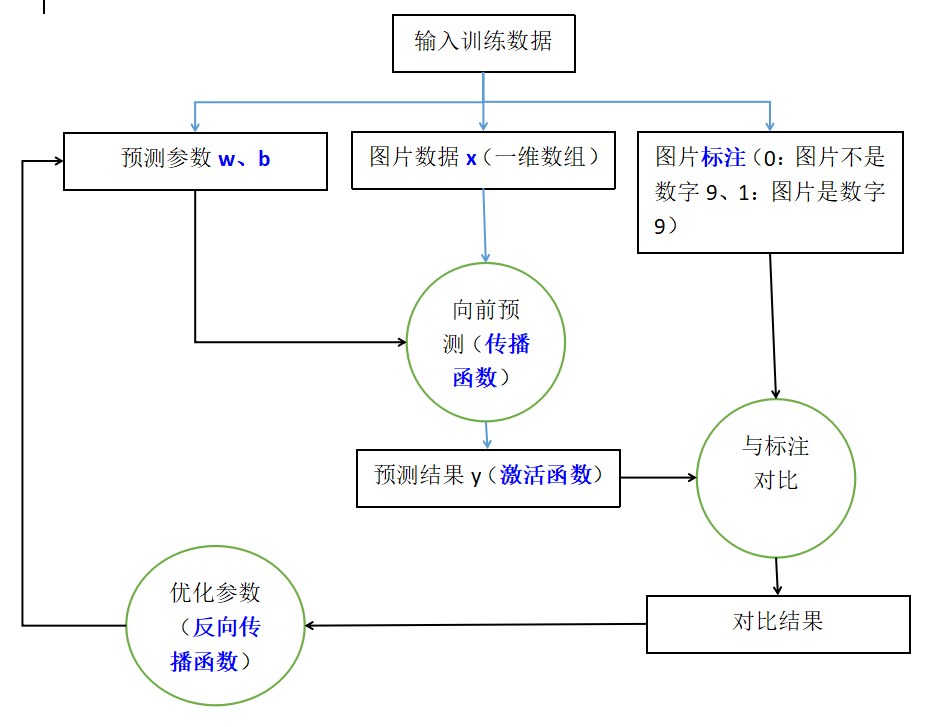
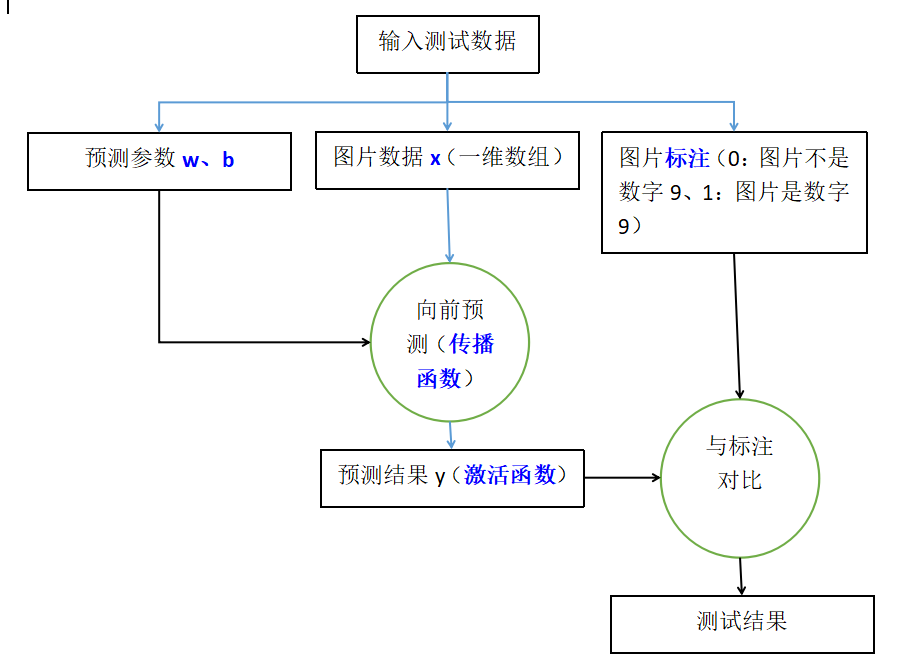
目前为止,一切都还比较难以理解,但只需要建立下面几个模糊的概念:
1、图片是以一维数组的形式传入神经元,每一张图片由784个像素组成,即一维数组的长度为784
2、神经元通过一个叫“传播函数”的东西尝试预测输入的图片是否是数字9
3、传播函数的原理是通过参数w和b与输入x做运算得到结果a
4、结果a又需要通过一个叫“激活函数”的东西来调整其输出,使其变为我们需要的输出形式y
5、将输出y与真实的标注进行对比,并根据对比结果使用“反向传播函数”来优化w和b
6、最终,传播函数结合最优的参数w和b就能做所谓的“AI识图”了(从一堆输入里识别出手写数字9)
五、传播函数
传播函数的数学公式如下,其中w叫权重、b叫偏置。
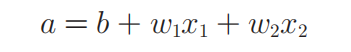
权重w的意义在于体现出x的那些像素比较重要,比如优化后的w1较w2值更大,则说明x1较x2更重要,体现在图片上则x1更多可能是数字的组成部分,x2更多可能是背景。b的意义在于调整神经元向下传递信号的难易程度,要讲清楚w和b就需要从感知机开始了,这个我们以后再说,这里只需要记住传播函数中,用权重w乘以x并加上偏置b就能知道输入x是否为一张“手写的数字9”图片。
上面的公式看起来挺简单的,但实际操作中又有所不同。
1)输入x有784个元素
上面的传播函数公式中,输入x只有两个元素,对于我们这里使用的图片,需要的是784个输入,所以实际公式应为:
a = b + w1x1 + w2x2 + w3x3 + ...... + w784x784
相应的参数w也有784个元素,所以初始化时我们将w生成为一个(784,1)的数组。
2)一次输入6000张图片
我们在训练时需要输入6000张图片,最直观的应该是写一个for循环,循环6000次即可,但有时可能训练图片是10万、100万,那写个for循环效率就太低了。好在python提供了非常强大的数据处理方式即“矩阵乘积”一次性完成所有计算,具体原理就不细讲,只需要知道我们将待处理数据train_img由(6000,784)转置成(784,6000)的形式就是为了做矩阵的乘积,一次将6000张图片计算完毕。下图是矩阵乘积的示意。
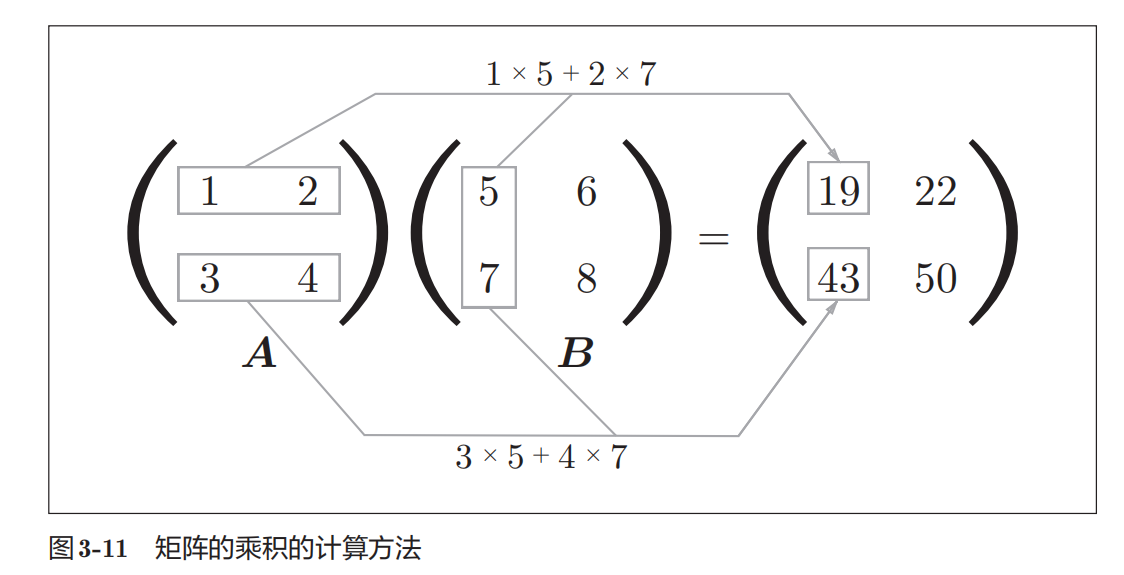
总的来讲,通过矩阵乘积我们可以一次计算出6000个a,并将结果放入名为A的新矩阵中。
在python中实现上述矩阵乘积非常简洁,如下:
A = np.dot(W.T, X)+b
其中W.T是权重w的转置,X是输入(已经转置过的),b是偏置,A是计算结果。np.dot()的作用就是将两个矩阵相乘。需要注意的是X是6000个输入,A是6000个计算结果。因为权重W和X都是转置后再相乘的,所以最终结果与6000个for循环一致。
3)总结一下
W的数据格式是(784,1),转置后是(1,784)
X的数据格式是(784,6000),6000代表一次计算6000个图片的结果
A的数据格式是(1,6000),A是6000个图片的计算结果合集
图解一下计算过程大概是这样:

六、激活函数
前面我们解析了传播函数,它的实现代码是这样:
A = np.dot(W.T, X)+b
一次计算的结果大概是这样,其中每一个A都是一张图片与参数w、b的计算结果。

参数w、b优化数百次后再次计算A的结果大概是下图这样(先不要考虑如何优化),可以看到大部分数值都还是负数(而且越负越多),但有部分值已变为正值。其实随着参数的优化,数字9的图片计算结果会越来越向正数靠拢,而非数字9的图片计算结果会越来越向负数靠拢。这里先不讲原因,但可以先建立这样的映像“当a的值大于0时图片为数字9,a的值小于0时图片不为数字9”且“a的值越大于0则图片越有可能是数字9,a的值越小于0则图片越有可能不是数字9”。
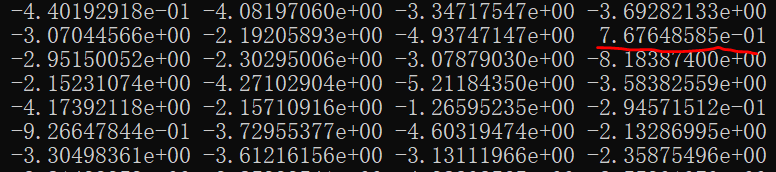
但是这样的表述无法与“标签”进行比较,因为标签的值是0或1(0代表非数字9、1代表是数字9)。如果A的值是0~1的一个数字,那A与标签值进行比较,我们就能知道当前被识别图片是更趋向于数字9抑或更趋向于不是数字9。激活函数sigmoid就是这么个作用,它将A的值“映射”到区间0~1方便与标签进行比较。sigmoid函数式如下:
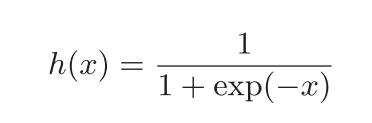
使用python也非常易于实现

从数学上来解析这个式子,我们可以知道:
1)当x为0时,h(x)输出为0.5。
2)当x趋向于负数,且负的越多则h(x)趋向于0
3)当x趋向于正数,且正的越多则h(x)趋向于1
从数学的角度来理解,它是将X轴的值映射到了Y轴,如此实现了输入值在0~1区间上的转化。有了激活函数,我们就可以方便地与标签进行对比,以此为基础实现参数的优化。激活函数sigmoid画成图像就是这样(需要注意,sigmoid只是激活函数的一种,还有其他类型的激活函数,原理一样但是映射的值不一样):
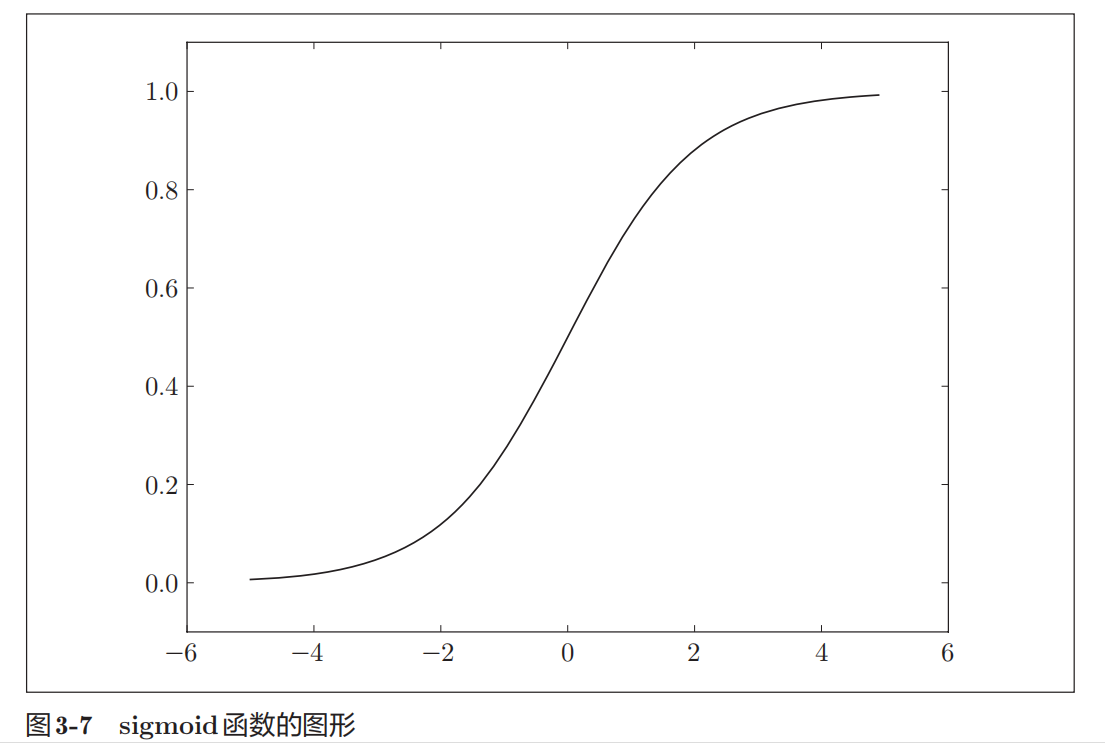
七、反向传播函数
我们先回顾一下前面的内容:
1)使用传播函数可以用图片中的每一个像素与权重w和阈值b做运算,计算结果a表明该图片是否为手写数字9(a大于0是手写数字9,a小于0就不是手写数字9)
2)使用激活函数sigmoid可以将a的值映射到0~1的区间,计算结果y表明该图片是否为手写数字9(y大于0.5是手写数字9,y小于0.5就不是手写数字9)
虽然前面我们讲的很详细很复杂了,反向传播函数依旧很难以理解。大体上我们可以建立这样的映像:
1)传播函数通过w、b计算出A,通过激活函数又计算出Y
2)反向传播函数通过Y计算出dw和db
3)使用dw和db,通过一种叫“梯度下降”的方法得到新的w和b
4)使用更新后的w和b重复前面的运算过程
需要注意的是,“梯度下降”是一种更新w和b的方法,不同模型可能会使用不同的方法来更新w和b,只是我们这里使用这个比较容易理解的方法而已。其次我们不讨论“反向传播”的原理,只是对实现过程做分析(因为原理看不懂啊!)
前面激活函数中我们讲过,使用激活函数的目的是将A的值转为0~1的区间值Y,方便与标签进行对比。对比的方法很直接,使用Y减去标签值即可:
dZ = Y - train_label
其中Y是激活函数的输出,代表着图片是否接近数字9或更远离数字9。train_label就是所有训练图片的标签值,是判断Y的依据。dZ是计算结果。截取某一次训练的数据大概是下面这样:
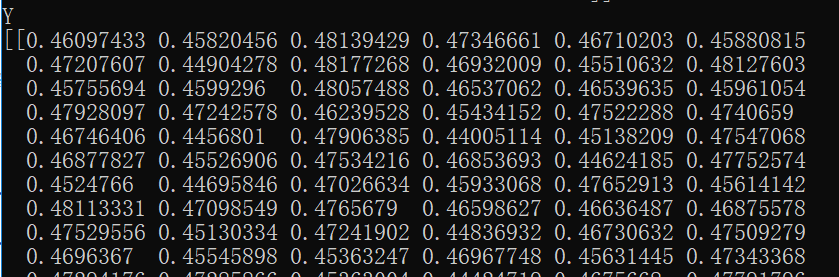

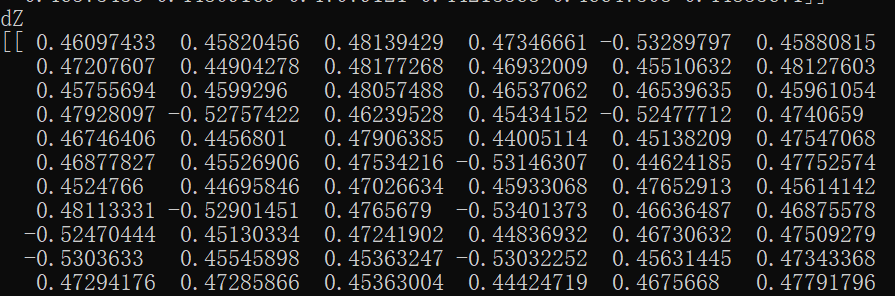
通过上面的实例演示,我们会发现“若图片真的是数字9,则Y减去train_label的值会变为负数(因为train_label值为1),若图片不是数字9,则Y减去train_label的值是不变的(因为train_label的值为0)”。
下面依据dZ的值我们来计算出dw和db。
dw = np.dot(train_img, dZ.T)/m
db = np.sum(dZ)/m
计算方法就很简单,但是具体含义呢?为什么dw可以用来更新参数w,db可以用来更新参数b?
我们知道train_img是训练用的图片数据,前面已经将其转置为(784,6000)这样的数据形式,dZ由Y和train_label相减得来,所以dZ的数据形式为(1,6000),转置后为(6000,1)。所以train_img与dZ.T的乘积结果dw为(784,1)这样的数据形式,dw刚好契合了权重w的数据形式(784,1)和图片像素的数量784。
dw计算结果示意如下图,我们会发现部分dw的值向正数越来越大,部分dw值向负数越来越小。

对于dZ与train_img的乘积dw,我们可以用一张图来描述这个过程:

可以看到,dw的值是其实是6000个图片中,某一个像素值与dZ的平均乘积。以dw1为例,它是6000张图片中,所有图片的第一个像素值,与dZ相乘,再取平均值。我们再回顾一下前面的计算,dZ=Y-train_label。dZ中每一个元素就代表着某一个图片是更倾向于是数字9(负数)或更倾向于不是数字9(正数)。所以,对于dZ与train_img的乘积dw,我们可以这么理解:
【若dw的某一个元素值为负,且负的越多说明图片中该像素点在“图片为数字9的判断中,权重更大”。若dw的值为正,且正的越多说明图片中该像素点在“图片为数字9的判断中,权重更小”。】
那么相应的,我们是不是可以用dw作为权重w的更新参考?
db的含义我还没有完全理解,这里只是简单说明下,db是dZ的和取平均。可以想到,若训练图片中有更多的数字9,则db的值偏向于负值,若训练图片中有更多的非9,则db的值偏向于正值。
更新参数
前面我们通过传播函数和激活函数得到图片为数字9的概率,又通过反向传播函数计算出了dw和db。有了dw和db,我们就可以更新权重w和偏置b。
w = w - learning_rate*dw
b = b - learning_rate*db
这里的learning_rate叫做学习率,其实就是用来调整dw的幅度,使得w的值可以合理的增加或减少。这里需要注意的是,对于比较重要的像素,其dw是负值,所以这里是用w减去dw(增加该像素的权重)。learning_rate太大或太小都不行,一般就看学习效果如何来手动调整,那如何看学习的效果呢,这就要讲到最后一个函数“损失函数”了。
八、损失函数
我们使用的损失函数公式如下:
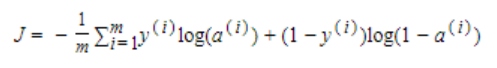
实现代码如下:
cost = -np.sum(train_label*np.log(Y)+(1-train_label)*np.log(1-Y)) / m
其中Y是使用激活函数处理后的数值,即训练图片是否为数字9在0~1上的概率分布。cost值的意义在于计算出最新Y与标注train_label间的误差。实质上这个值在本文中仅作为参考,看当前运算是否延正常路径进行中(cost值会越来越小)。
九、汇总回顾
前面我们详细叙述了神经元的4个函数,这里我们就依据这四个函数实现一个单神经元“手写数字9”识别的AI。完整代码在文末有下载方式。
#下载数据集,会下载6W个训练数据核1W个测试数据
init_mnist()
#加载数据集 数据集包括一张图片和一个正确标注
(train_img,train_label),(test_img,test_label) = load_mnist(normalize=True, flatten=True, one_hot_label=False)
#将label不是9的数据全部转为0,将9转为1
train_label = np.where(train_label==9,1,0)
test_label = np.where(test_label==9,1,0)
#修改数组的大小
train_img = np.resize(train_img,(6000,train_img.shape[1]))
train_label = np.resize(train_label,(6000,1))
test_img = np.resize(test_img,(1000,test_img.shape[1]))
test_label = np.resize(test_label,(1000,1))
#需要将数据进行转置
train_img = train_img.T
train_label = train_label.T
test_img = test_img.T
test_label = test_label.T
#sigmoid函数
def sigmoid(x):
s = 1/(1+np.exp(-x))
return s
#初始化权重数组w和偏置b(默认为0)
def initialize_with_zeros(dim):
w = np.zeros((dim,1))#全零的数组
b = 0
return w,b
#通过Y和标注计算成本
def costCAL(img, label, Y):
m = img.shape[1]
cost = -np.sum(train_label*np.log(Y)+(1-train_label)*np.log(1-Y)) / m
return cost
#向前传播得到Y
def propagate(w, b, img):
m = img.shape[1]
#向前传播
A = np.dot(w.T, img)+b
#使用激活函数将A的值映射到0~1的区间
Y = sigmoid(A)
return Y
#反向传播得到dw、db
def back_propagate(Y, img, label):
m = img.shape[1]
dZ = Y - label
dw = np.dot(img,dZ.T)/m
db = np.sum(dZ)/m
return dw,db
#通过梯度下降法更新w和b
def optimize(img,label,w,b,num_iterations,learning_rate,print_cost):
#梯度下降法,循环num_iterations次找到最优w和b
for i in range(num_iterations):
#向前传播一次
Y = propagate(w, b, img)
#计算成本
cost = costCAL(img, label, Y)
#反向传播得到dw、db
dw,db = back_propagate(Y, img, label)
#更新w和b
w = w - learning_rate*dw
b = b - learning_rate*db
#每100次输出一下成本
if i%100 ==0:
if print_cost:
print('优化%i次后成本是:%f' %(i,cost))
return w, b
#预测函数
def predict(w, b, img):
m = img.shape[1]
Y_prediction = np.zeros((1,m))
#向前传播得到Y
Y = propagate(w, b, img)
for i in range(Y.shape[1]):
#若Y的值大于等于0.5就认为该图片为数字9,否则不是数字9
if Y[0,i] >= 0.5:
Y_prediction[0,i] = 1
return Y_prediction
#按训练图片的数量生成w和b,
w,b = initialize_with_zeros(train_img.shape[0])
#通过梯度下降法更新w和b
w, b = optimize(train_img,train_label,w,b,2000,0.005,True)
Y_prediction_train = predict(w, b, train_img)
Y_prediction_test = predict(w, b, test_img)
print('对训练图片的预测准确率为:{}%'.format(100-np.mean(np.abs(Y_prediction_train - train_label))*100))
print('对测试图片的预测准确率为:{}%'.format(100-np.mean(np.abs(Y_prediction_test - test_label))*100))
十、总结
本文大概对神经网络中的四个核心函数做了一些解析,还缺少一些数学上的推导留到以后再总结吧。汇总一下前面的信息:
1)图片以矩阵的形式导入程序,一次可以输入数千、数万张图片批量处理
2)通过矩阵的乘积来计算输入图片、权重w、偏置b的值,一次得到6000个图片的传播结果A(传播函数)
3)通过激活函数将A的值映射到0~1的区间得到Y,Y体现的是导入的图片是数字9的概率(激活函数)
4)通过Y与导入的图片数据做运算可以得到dw和db,dw体现的是某像素在判断图片是否为数字9的作用大不大(反向传播)
5)通过将dw加到w上来更新w,可以让更重要的像素得到更大的权重(梯度下降)
6)通过Y与导入的图片标注做运算可以得到cost,cost体现的是使用当前的w和b做预测与真实结果之间的误差(损失函数)
7)前面的步骤重复2000次,就得到了最终的w、b。重复的次数其实没有具体的限制,只需要平衡好训练的次数和时间成本即可
如果需要完整的代码,请关注公众号“零基础爱学习”回复“AI4”就能获取代码文件了。以后还会继续推送零基础入门的文章。
