一、序言
动量梯度下降也是一种神经网络的优化方法,我们知道在梯度下降的过程中,虽然损失的整体趋势是越来越接近0,但过程往往是非常曲折的,如下图所示:

特别是在使用mini-batch后,由于单次参与训练的图片少了,这种“曲折”被放大了好几倍。前面我们介绍过L2和dropout,它们要解决的也是“曲折”的问题,不过这种曲折指的是求得的W和b过于拟合训练数据,导致求解曲线很曲折。动量梯度下降所解决的曲折指的是求得的dw、db偏离正常值导致成本时高时低,求得最优W和b的过程变慢。
二、指数加权平均
动量梯度下降是相较于普通的梯度下降而言,这里所谓的动量其实说的是动量效应,最早是在经济学领域提出的:
“指股票的收益率有延续原来的运动方向的趋势”
其实换个名字叫“惯性效应”更好理解,即事物的发展趋势是有惯性的。
那应用到神经网络的优化中,就是在计算dw、db时参考下之前的计算结果,具体操作起来的方法就叫“指数加权平均”,示例如下:
dw0 = 1
dw1 = 1.2,指数加权平均后:dw1 = 0.9*dw0 + 0.1*dw1 = 1.05
dw2 = 1.5,指数加权平均后:dw2 = 0.9*dw1 + 0.1*dw2 = 1.095
dw3 = 1.8,指数加权平均后:dw3 = 0.9*dw2 + 0.1*dw3 = 1.1655
上面的示例就是指数加权平均,看起来似乎只是将dw变化的幅度减小了,下面我们模拟一次曲折
dw4 = -1,指数加权平均后:dw4 = 0.9*dw3 + 0.1*dw4 = 0.94895
在dw4的优化中,原本w应该是减去1的,但现在是加上了0.94895,即w还是沿着前面dw0至3的路径在优化,有效地降低了dw4的影响。这种使用指数加权平均计算dw并更新w的方式就是动量梯度下降。
三、动量梯度下降的实现
我们可以用一个公式来描述指数加权平均:
vDW1 = beta*vDW0 + (1-beta)*dw1
vDb1 = beta*vDb0 + (1-beta)*db1
我们使用vDW和vDb来记录指数加权平均值,beta值由我们设定,一般是0.9(这个数值代表了历史数据对当前值的影响,可以自己调整看看效果不一定就一定要0.9)。计算出指数加权平均值后,我们再将这个值应用到梯度下降中即是所谓的“动量梯度下降”了。
W = W - learning_rate*vDw
b = b - learning_rate*vDb
四、回顾
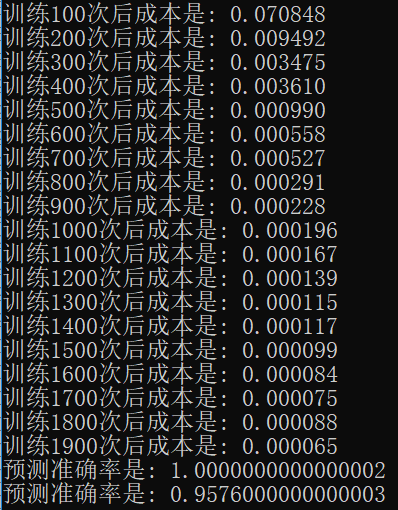
本节就简单说了下动量梯度下降,可以对比看下应用前和应用后的效果:
应用前
应用后:
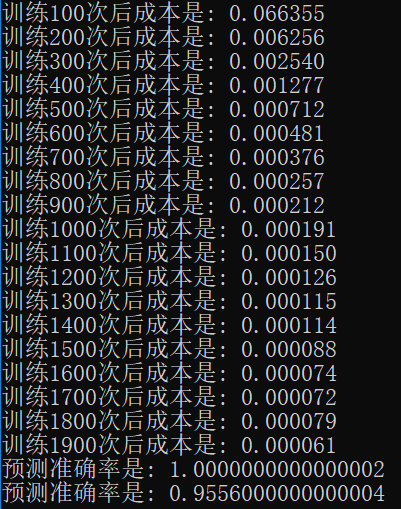
可以看到使用动量梯度下降后,损失是有一点收窄的效果,虽然最终预测准确率不一定就边得更好了。具体实现代码请关注公众号“零基础爱学习”回复AI12获取。
