第二部分、后缀树
2.1、后缀树的定义
后缀树(Suffix tree)是一种数据结构,能快速解决很多关于字符串的问题。后缀树的概念最早由Weiner 于1973年提出,既而由McCreight 在1976年和Ukkonen在1992年和1995年加以改进完善。
后缀,顾名思义,甚至通俗点来说,就是所谓后缀就是后面尾巴的意思。比如说给定一长度为n的字符串S=S1S2..Si..Sn,和整数i,1 <= i <= n,子串SiSi+1...Sn便都是字符串S的后缀。
以字符串S=XMADAMYX为例,它的长度为8,所以S[1..8], S[2..8], ... , S[8..8]都算S的后缀,我们一般还把空字串也算成后缀。这样,我们一共有如下后缀。对于后缀S[i..n],我们说这项后缀起始于i。
S[1..8], XMADAMYX, 也就是字符串本身,起始位置为1
S[2..8], MADAMYX,起始位置为2
S[3..8], ADAMYX,起始位置为3
S[4..8], DAMYX,起始位置为4
S[5..8], AMYX,起始位置为5
S[6..8], MYX,起始位置为6
S[7..8], YX,起始位置为7
S[8..8], X,起始位置为8
空字串,记为$。
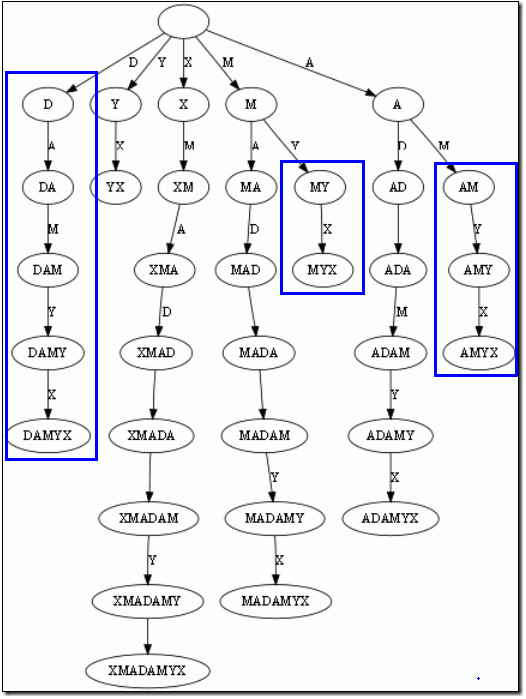
而后缀树,就是包含一则字符串所有后缀的压缩Trie。把上面的后缀加入Trie后,我们得到下面的结构:
仔细观察上图,我们可以看到不少值得压缩的地方。比如蓝框标注的分支都是独苗,没有必要用单独的节点同边表示。如果我们允许任意一条边里包含多个字 母,就可以把这种没有分叉的路径压缩到一条边。另外每条边已经包含了足够的后缀信息,我们就不用再给节点标注字符串信息了。我们只需要在叶节点上标注上每项后缀的起始位置。于是我们得到下图:
这样的结构丢失了某些后缀。比如后缀X在上图中消失了,因为它正好是字符串XMADAMYX的前缀。为了避免这种情况,我们也规定每项后缀不能是其它后缀的前缀。要解决这个问题其实挺简单,在待处理的子串后加一个空字串就行了。例如我们处理XMADAMYX前,先把XMADAMYX变为 XMADAMYX$,于是就得到suffix tree--后缀树了,如下图所示:

2.2、后缀树与回文问题的关联
那后缀树同最长回文有什么关系呢?我们得先知道两个简单概念:
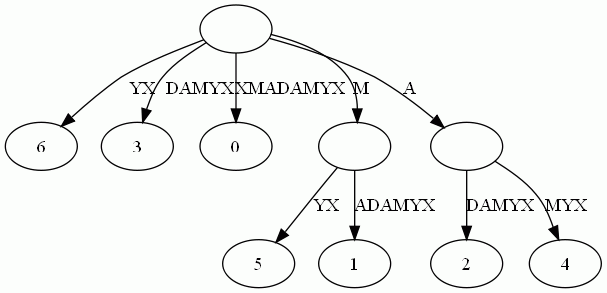
- 最低共有祖先,LCA(Lowest Common Ancestor),也就是任意两节点(多个也行)最长的共有前缀。比如下图中,节点7同节点10的共同祖先是节点1与借点,但最低共同祖先是5。 查找LCA的算法是O(1)的复杂度,这年头少见。代价是需要对后缀树做复杂度为O(n)的预处理。
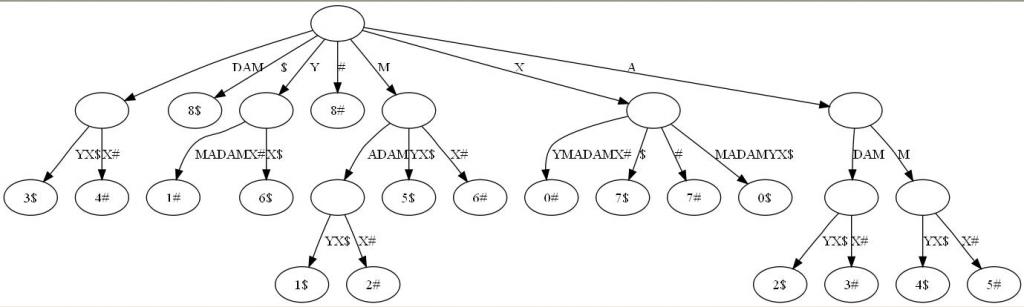
- 广义后缀树(Generalized Suffix Tree)。传统的后缀树处理一坨单词的所有后缀。广义后缀树存储任意多个单词的所有后缀。例如下图是单词XMADAMYX与XYMADAMX的广义后缀 树。注意我们需要区分不同单词的后缀,所以叶节点用不同的特殊符号与后缀位置配对。
2.3、最长回文问题的解决
有了上面的概念,本文引言中提出的查找最长回文问题就相对简单了。咱们来回顾下引言中提出的回文问题的具体描述:找出给定字符串里的最长回文。例如输入XMADAMYX,则输出MADAM。
思维的突破点在于考察回文的半径,而不是回文本身。所谓半径,就是回文对折后的字串。比如回文MADAM 的半径为MAD,半径长度为3,半径的中心是字母D。显然,最长回文必有最长半径,且两条半径相等。还是以MADAM为例,以D为中心往左,我们得到半径 DAM;以D为中心向右,我们得到半径DAM。二者肯定相等。因为MADAM已经是单词XMADAMYX里的最长回文,我们可以肯定从D往左数的字串 DAMX与从D往右数的子串DAMYX共享最长前缀DAM。而这,正是解决回文问题的关键。现在我们有后缀树,怎么把从D向左数的字串DAMX变成后缀 呢?
到这个地步,答案应该明显:把单词XMADAMYX翻转(XMADAMYX=>XYMADAMX,DAMX就变成后缀了)就行了。于是我们把寻找回文的问题转换成了寻找两坨后缀的LCA的问题。当然,我们还需要知道 到底查询那些后缀间的LCA。很简单,给定字符串S,如果最长回文的中心在i,那从位置i向右数的后缀刚好是S(i),而向左数的字符串刚好是翻转S后得到的字符串S‘的后缀S'(n-i+1)。这里的n是字符串S的长度。
可能上面的阐述还不够直观,我再细细说明下:
1、首先,还记得本第二部分开头关于后缀树的定义么: “先说说后缀的定义,顾名思义,甚至通俗点来说,就是所谓后缀就是后面尾巴的意思。比如说给定一长度为n的字符串S=S1S2..Si..Sn,和整数i,1 <= i <= n,子串SiSi+1...Sn便都是字符串S的后缀。”
以字符串S=XMADAMYX为例,它的长度为8,所以S[1..8], S[2..8], ... , S[8..8]都算S的后缀,我们一般还把空字串也算成后缀。这样,我们一共有如下后缀。对于后缀S[i..n],我们说这项后缀起始于i。
S[1..8], XMADAMYX, 也就是字符串本身,起始位置为1
S[2..8], MADAMYX,起始位置为2
S[3..8], ADAMYX,起始位置为3
S[4..8], DAMYX,起始位置为4
S[5..8], AMYX,起始位置为5
S[6..8], MYX,起始位置为6
S[7..8], YX,起始位置为7
S[8..8], X,起始位置为8
空字串,记为$。
2、对单词XMADAMYX而言,回文中心为D,那么D向右的后缀DAMYX假设是S(i)(当N=8,i从1开始计数,i=4时,便是S(4..8));而对于翻转后的单词XYMADAMX而言,回文中心D向右对应的后缀为DAMX,也就是S'(N-i+1)((N=8,i=4,便是S‘(5..8)) 。此刻已经可以得出,它们共享最长前缀,即LCA(DAMYX,DAMX)=DAM。有了这套直观解释,算法自然呼之欲出:
- 预处理后缀树,使得查询LCA的复杂度为O(1)。这步的开销是O(N),N是单词S的长度 ;
- 对单词的每一位置i(也就是从0到N-1),获取LCA(S(i), S‘(N-i+1)) 以及LCA(S(i+1), S’(n-i+1))。查找两次的原因是我们需要考虑奇数回文和偶数回文的情况。这步要考察每坨i,所以复杂度是O(N) ;
- 找到最大的LCA,我们也就得到了回文的中心i以及回文的半径长度,自然也就得到了最长回文。总的复杂度O(n)。
上面大致描述了后缀树的基本思路。要想写出实用代码,至少还得知道下面的知识:
- 创建后缀树的O(n)算法。此算法有很多种,无论Peter Weiner的73年年度最佳算法,还是Edward McCreight1976的改进算法,还是1995年E. Ukkonen大幅简化的算法(本文第4部分将重点阐述这种方法),还是Juha Kärkkäinen 和 Peter Sanders2003年进一步简化的线性算法,都是O(n)的时间复杂度。至于实际中具体选择哪一种算法,可依实际情况而定。
- 实现后缀树用的数据结构。比如常用的子结点加兄弟节点列表,Directed 优化后缀树空间的办法。比如不存储子串,而存储读取子串必需的位置。以及Directed Acyclic Word Graph,常缩写为黑哥哥们挂在嘴边的DAWG。
2.4、后缀树的应用
后缀树的用途,总结起来大概有如下几种
- 查找字符串o是否在字符串S中。
方案:用S构造后缀树,按在trie中搜索字串的方法搜索o即可。
原理:若o在S中,则o必然是S的某个后缀的前缀。
例如S: leconte,查找o: con是否在S中,则o(con)必然是S(leconte)的后缀之一conte的前缀.有了这个前提,采用trie搜索的方法就不难理解了。 - 指定字符串T在字符串S中的重复次数。
方案:用S+’$'构造后缀树,搜索T节点下的叶节点数目即为重复次数
原理:如果T在S中重复了两次,则S应有两个后缀以T为前缀,重复次数就自然统计出来了。 - 字符串S中的最长重复子串
方案:原理同2,具体做法就是找到最深的非叶节点。
这个深是指从root所经历过的字符个数,最深非叶节点所经历的字符串起来就是最长重复子串。
为什么要非叶节点呢?因为既然是要重复,当然叶节点个数要>=2。 - 两个字符串S1,S2的最长公共部分
方案:将S1#S2$作为字符串压入后缀树,找到最深的非叶节点,且该节点的叶节点既有#也有$(无#)。
后缀树的代码实现,下期再续。第二部分、后缀树完。