深度网络模型压缩综述
文献来源:雷杰,高鑫,宋杰,王兴路,宋明黎.深度网络模型压缩综述[J].软件学报,2018,29(02):251-266.
摘要: 深度网络近年来在计算机视觉任务上不断刷新传统模型的性能,已逐渐成为研究热点.深度模型尽管性能强大,然而由于参数数量庞大、存储和计算代价高,依然难以部署在受限的硬件平台上(如移动设备).模型的参数在一定程度上能够表达其复杂性,相关研究表明,并不是所有的参数都在模型中发挥作用,部分参数作用有限、表达冗余,甚至会降低模型的性能.首先,对国内外学者在深度模型压缩上取得的成果进行了分类整理,依此归纳了基于网络剪枝、网络精馏和网络分解的方法;随后,总结了相关方法在多种公开深度模型上的压缩效果;最后,对未来的研究可能的方向和挑战进行了展望.
一、网络剪枝
网络剪枝按剪枝粒度(pruning granularities)可分为4类,如图所示。
- 中间隐层(layer)剪枝
- 通道(feature map/channel/filter)剪枝
- 卷积核(kernel)剪枝
- 核内权重(intra kernel weight)剪枝
- 单个权重剪枝

其中,Feature Map/Channel 都指网络中一层产生的特征图张量的一个通道.Filter是网络中的权重参数,Feature Map 是网络输出,在网络剪枝中两者等价,因为减去一个Filter 会导致少产生一个Feature Map。
从剪枝目标上分类,可分为减少参数/网络复杂度、减小过拟合/增加泛化能力/提高准确率、减小部署运行时间(test run-time)/提高网络效率以及减小训练时间等.不同的剪枝方法侧重也会有所不同,有的剪枝方法完全依赖网络参数,剪枝后不需要调优恢复准确率;有的剪枝方法则只适用于全连接层剪枝.
二、剪枝方法
2.1 单个权重粒度
将剪枝看作是将小权重置零的操作,手术恢复则相当于找到相似权重补偿被置零的权重造成的激活值损失.两个权重的相似程度定义如下:
其中:
- (varepsilon_{i,j}=W_i-W_j),用来度量输入节点i 和节点j 之间权重矢量的相似程度;
- (<a^2_j>)为输出节点 j 权重的均值,表示节点 j 与 0 的接近程度.
整体剪枝步骤为:对所有可能权重矢量的组合,初始化时计算(s_{i,j})构成的矩阵,找到矩阵中最小的一项((i^′,j^′)),删去第(j^′)个神经元,并更新权重(a_{j^′}←a_{i^′}+a_{j^′});然后,再通过简单的删除与叠加操作更新S矩阵,就完成了一次剪枝与手术恢复.
2.2 核内权重粒度
在第2.1 节中,网络中的任意权重被看作是单个参数并进行随机非结构化剪枝,该粒度的剪枝导致网络连接不规整,需要通过稀疏表达来减少内存占用,进而导致在前向传播预测时,需要大量的条件判断和额外空间来标明零或非零参数的位置,因此不适用于并行计算。
Anwer等人(^{[1]})提出了结构化剪枝的概念,可以很方便地使用现有的硬件和BLAS等软件库进行矩阵相乘,利用剪枝后网络的稀疏性来加速网络效率.粗粒度剪枝,如通道粒度和卷积核粒度本身就是结构化的,他的创新之处在于提出了核内定步长粒度(intra kernel strided sparsity),将细粒度剪枝转化为结构化剪枝.
该方法首先随机初始化步长m 和偏置n.考虑到卷积核一般选取(k×k) 的方阵,起始项的下标((i,j))选为(i=j=n),则遍历的位置如((n,n),(n+m,n),(n,n+m))等.核内定步长粒度剪枝的关键思想在于:作用到同一输入特征图上的Kernel必须采用相同的步长和偏置.当卷积层不是稠密连接时,作用在不同特征图上的Kernel步长与偏置可以不同,但是,如果卷积层的连接为一般的全连接(即一个特征图需要被所有Kernel作用一遍再加和生成新的特征图),那么所有Kernel必须采用相同的步长和偏置.这是由于只有相同的步长与偏置,才能在Lowering(cuDNN 中的im2col)操作时形成大小匹配的Lowering Kenrel Matrix,从而减小核矩阵和特征图矩阵的大小,极大地节约计算资源.
2.3 卷积核粒度与通道粒度
具体步骤是减去第i层的filter,进而减去第i层产生的部分Feature Map和第i+1 层的部分Kernel.
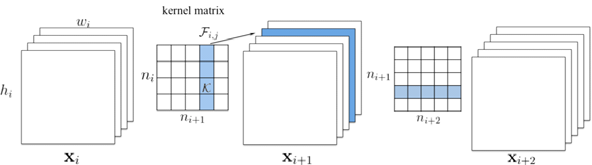
图中第i层卷积层的卷积核矩阵可以看作由(n_i×n_{i+1})个k×k的卷积核组成(即图中每一个网格).一个Filter作用在全部(n_i)个输入Feature Map(即为Channel)上,产生1个新的Feature Map,因而(n_{i+1})个Filter产生(n_{i+1})个Feature Map.从而Filter将三维输入(x_i)转换为三维输出(x_{i+1}).
FeatureMap 粒度的显著性度量也可以简单地选取Filter权重和作为显著性度量,关键在于如何确定剪枝数量以及如何对网络整体剪枝(^{[2]}).Li 等人提出了全局贪婪剪枝(holistic Global pruning)(^{[3]}),选取Filter权重和作为显著性度量.对每一层中的Filter按照显著性从大到小排序,进而画出权重和关于排序后下标的曲线.若曲线陡峭,则在这一层减去更多的Filter;若曲线平缓,则减去较少的Filter,为剪枝数量提供了经验性的指导.具体剪枝数量则作为超参数优化,在每一层剪枝数量确定之后,开始对整个网络进行全局贪婪剪枝.全局是指在全部剪枝完成后,再通过一次训练恢复准确率;贪婪是指减去上一层Filter后,更新下一层部分Kernel内的权重,从而在下一层剪枝时,已经减掉的Kernel不再对Filter贡献任何显著性.
三、网络蒸馏
网络蒸馏是指利用大量未标记的迁移数据(transfer data),让小模型去拟合大模型,从而让小模型学到与大模型相似的函数映射.网络蒸馏可以看成在同一个域上迁移学习(^{[4]})的一种特例,目的是获得一个比原模型更为精简的网络。大模型作为教师模型(teacher model)是预先训练好的,小模型作为学生模型(student model),由教师模型指导,步骤①首先由数据生成器生成大量的迁移数据(transfer data),分别送入教师模型和学生模型中.步骤②将教师模型的输出作为真实值,衡量学生模型的输出与它之间的损失.步骤③通过梯度下降等方法更新学生模型的权重,使得学生模型的输出和教师模型的输出更加接近,从而达到利用小模型拟合大模型的效果.

参考文献
[1] Anwar S, Hwang K, Sung W. Structured pruning of deep convolutional neural networks. ACM Journal on Emerging Technologies in Computing Systems (JETC), 2017,13(3):Article No.32. [doi: 10.1145/3005348]
[2] Figurnov M, Ibraimova A, Vetrov DP, Kohli P. PerforatedCNNs: Acceleration through elimination of redundant convolutions. In:Proc. of the Advances in Neural Information Processing Systems (NIPS). Barcelona: IEEE, 2016. 947−955.
[3] Li H, Kadav A, Durdanovic I, Samet H, Graf HP. Pruning filters for efficient ConvNets. In: Proc. of the Int’l Conf. on Learning and Representation (ICLR). IEEE, 2017. 34−42.
[4] Pan SJ, Yang Q. A survey on transfer learning. IEEE Trans. on Knowledge and Data Engineering, 2010,22(10):1345−1359. [doi: 10.1109/TKDE.2009.191]