前言
第四章——算法初步
一些初级的/经典的算法思想:
排序/散列/递归/贪心/二分/two pointer;
尽量每一篇不要篇幅过长,所以本章大概分3~4篇来记录;
本篇总结自《算法笔记》4.1-4.2,主要记录排序和散列。
正文
知识点1:排序
冒泡排序已经在第二章讲过了 [传送门]
选择排序(选择排序有很多种,这里讲最基础常用的一种)
总体说:从待排序部分挑出最小的元素与待排序部分首位交换,并把首位加入已排序部分,重复n-1次。示意图如下
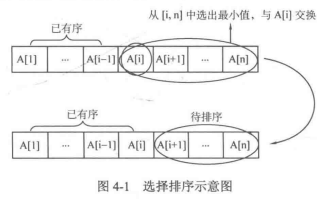
具体说(也可直接下面看代码):
比如5个数,一开始5个都属于待排序部分,选出最小的放到待排序部分的第1位(整体的第1位),然后第1位算作已排序部分,此时有4个属于待排序部分,1个属于已排序;1
再从待排序部分(4个)中选出最小的,放到待排序部分的第1位(整体的第2位),第1位进入已排序部分的末尾,此时有3个属于待排序部分,2个属于已排序;2
再从待排序部分(3个)中选出最小的,放到待排序部分的第1位(整体的第3位),第1位进入已排序部分的末尾,此时有2个属于待排序部分,3个属于已排序;3
再从待排序部分(2个)中选出最小的,放到待排序部分的第1位(整体的第4位),第1位进入已排序部分的末尾,此时有2个属于待排序部分,4个属于已排序;4
最后一个不用排了,肯定最小,共进行n-1次排序。
插入排序(插入排序也有很多种,这里先讲直接插入排序)
对比选择排序:
选择排序——待排序部分选最小放前面,累积出来已排序的部分。
插入排序——已排序部分选位置给待排序的数,待排序部分一个个插入到已排序部分中。
总体说:进行n-1趟操作(无视第一位),每趟操作都把待排序部分的第一个插入到已排序部分的正确位置。
具体说(也可直接下面看代码):
比如5个数,忽略第1个,因为1个元素必然是有序的,此时已排序1个,待排序4个,所以选择待排序中第一个,一般从后往前比较已排序部分第一个比他小的数,插在它后面。(为什么不是从前往后找第一个比它大的数插在前面?因为写代码方便)
插入第1个后,已排序已经有2个了,待排序有3个,继续取待排序3个中第一个,从已排序部分末尾往前比较到第一个比他小的数,插在这个比它小的数后面,
插入第2个后,已排序已经有3个了,待排序有2个,继续取待排序2个中第一个,从已排序部分末尾往前比较到第一个比他小的数,插在这个比它小的数后面,
插入第3个后,已排序已经有4个了,待排序有1个,取待排序1个,从已排序部分末尾往前比较到第一个比他小的数,插在这个比它小的数后面。
#include<cstdio> int showArr(int A[], int n){ for(int i = 0 ;i < n; i++){ printf("%d ",A[i]); } } /* 选择排序 */ int* selectSort(int A[], int n){ for(int i = 0; i < n; i++){ // 进行n趟操作 int k = i; /* 选出待排序部分最小值 */ for(int j = i; j < n; j++){ if(A[j] < A[k]){ k = j; } } /* 待排序部分 最小值与首位交换 */ int temp = A[i]; A[i] = A[k]; A[k] = temp; } return A; } /* 插入排序 */ int* insertSort(int A[], int n){ for(int i = 1; i < n; i++){ // 进行n-1趟排序 (数组下标为0~n-1) /* 暂存A[i],j从i开始往前枚举(i是待排序的第一位) */ int temp = A[i], j = i; /* 找到待插入位置j */ while(j > 0 && temp < A[j-1]){ // 只要待插入数小于枚举数 A[j] = A[j-1]; //枚举数后移 j--; } A[j] = temp; } return A; } int main(){ int x; int* result = &x; // 指针初始化 int maxn = 100; int a[maxn]; while(scanf("%d", &maxn) != EOF){//先读入数组长度 for(int i = 0; i < maxn; i++){//再读入maxn个数 scanf("%d", &a[i]); } result = insertSort(a, maxn); // 排序 //result = selectSort(a, maxn); showArr(result, maxn); // 输出结果 printf(" "); } return 0; }
以下方法可以获取数组A的长度,但作为参数传给函数后该方法失效 [原因], 所以要把数组长度作为参数传给函数。
int n = sizeof(A) / sizeof(A[0]); // 获取数组长度(数组传参后获取不到)
知识点2:排序题常用的sort函数
C++自带的sort函数
上机的时候大多只要得到排序的结果对排序算法无特殊要求,可以直接使用C++的sort函数(C中的qsort函数也可以但是要了解指针且不够sort简洁)[sort函数见第6章]
1)结构体排序
考试中通常不是简单的数字排序,而是附带很多信息的排序(为了方便把它们写到结构体后排序)
比如一个学生
struct Student{ char name[10]; // 姓名 char id[10]; // 准考证号 int score; // 分数 int r; // 排名 }stu[100010];
2)cmp函数编写
cmp函数提供sort函数的排序规则。
bool cmp(Student a, Student b){ if(a.score != b.score) return a.score > b.score; else return strcmp(a.name, b.name) < 0 } /*若成绩不等则成绩高的学生在前,若成绩相等则按姓名排序*/
注:其中strcmp函数是string.h头文件下的用来比较两字符串字典顺序大小的
strcmp的返回值不一定是-1或+1,不同编译器返回值不同
3)排名的实现
排完序后不能说完全实现了排名,还存在一个难点,即得分相同时,排名并列的情况。
解决方法:结构体定义时加上排名这一项
在数组排序完成后,用如下两种方法实现排名的计算:
stu[0].r = 1; // 先把数组第一个排名为1 for(int i = 1; i < n; i++){ if(stu[i].score == stu[i-1].score) stu[i].r = stu[i-1].r; // 分数相等,排名并列 else stu[i].r = i + 1; // 否则排名为当前下标+1 }
int r = 1; for(int i = 0; i < n; i++){ if(i > 0 && stu[i].score != stu[i-1].score) r = i + 1; // 直接输出r(题目不需要记录排名时) }
sort函数实例【PAT A1025】 PAT Ranking
#include<cstdio> #include<cstring> #include<algorithm> using namespace std; struct Student{ char id[15]; // 准考证号 int score; // 分数 int location_number; // 考场号 int local_rank; // 考场排名 }stu[30010]; bool cmp(Student a, Student b){ if(a.score != b.score) return a.score > b.score; else return strcmp(a.id, b.id) < 0; } int main(){ int n, k, num; // num为考生数 scanf("%d", &n); // 输入考场数 for(int i = 0; i < n; i++){ scanf("%d", &k); // 输入第i考场人数 /*录入当前考场的考生信息*/ for(int j = 0 ;j < k; j++){ scanf("%s %d", stu[num].id, &stu[num].score); // 记录准考证和分数 stu[num].location_number = i; // 记录考场号 num++; // 总考生数+1 } /* 将该考场的考生排序 */ sort(stu + num - k, stu + num, cmp); /* 该考场第1名的local_rank=1 */ stu[num-k].local_rank = 1; /* 考场内排名(以考场内第一名为标准) */ for(int j = num - k + 1; j < num; j++){ if(stu[j].score == stu[j-1].score){ stu[j].local_rank = stu[j-1].local_rank; // 若与前者分数相等则local_rank也相等 }else{ stu[j].local_rank = j + 1 - (num - k); // local_rank为本考场前面的人数 } } } printf("%d ", num); //输出总考生数 sort(stu, stu + num, cmp); // 总体排名 int r = 1; //暂存当前考生排名 /* 输出总排名 */ for(int i = 0; i < num; i++){ if(i > 0 && stu[i].score != stu[i-1].score){ r = i + 1; //与前一个人分数不同时,排名+1 } printf("%s", stu[i].id); printf("%d %d %d ", r, stu[i].location_number, stu[i].local_rank); } return 0; }
知识点3:散列
散列(hash)是一种用空间换时间的方法,很常用。
例1:给出N个数,再给出M个数,问这M个数是否分别在N个数中出现过
最简单的思路:M个每个都遍历一轮N个数,时间复杂度达到O(MN),当M和N都很大(105级别)时,系统无法承受。
运用散列的思路:设定布尔型数组hashTable[100010],用来在开始录入N个数的时候记录某个数是否出现过,假设当前录入的数是x,则把hashTable[x]=true,即表示x在这N个数中出现过,反之没有出现过。
对M个欲查询的数则直接找hashTable对应的值是否为true即可。
如此的时间复杂度只有O(M+N)【N次记录+M次查找】
#include<cstdio> const int maxn = 100010; bool hashTable[maxn] = {false}; //初始化为false(只赋第一个) int main(){ int n,m,x; scanf("%d%d", &n, &m); for(int i = 0; i < n; i++){ scanf("%d", &x); hashTable[x] = true; //数字x出现过 } for(int i = 0; i < m; i++){ scanf("%d", &x); if(hashTable[x] == true){ printf("YES "); }else{ printf("NO "); } } return 0; }
例1变形:给出N个数,再给出M个数,问这M个数分别在N个数中出现次数
只需把hashTable改成int型,录入N个数的时候对应的hashTable[x]++即可。

#include<cstdio> const int maxn = 100010; int hashTable[maxn] = {0}; int main(){ int n,m,x; scanf("%d%d", &n, &m); for(int i = 0; i < n; i++){ scanf("%d", &x); hashTable[x]++; //数字x出现次数增加 } for(int i = 0; i < m; i++){ scanf("%d", &x); printf("%d ", hashTable[x]); } return 0; }
总结:直接把输入的数作为数组下标,来对这个数的性质进行统计(务必掌握,非常实用的做法!)
该方法用空间换时间,把时间复杂度降到O(1)
缺陷:若录入的数超过了105(如1111111111),甚至变成了字符串(如“I Love You”),就不能作为数组下标了。
解决方法:需要由散列(hash),把这些各种各样的元素都转为规定范围内的数字。
散列的作用:将元素通过一个函数转化为整数,使得该整数尽量唯一的代表这个整数。[其中的函数称为散列函数H,如元素转换前为key,转换后则为H(key)]
知识点4:对整数进行散列的方法
直接定址法(恒等/线性)[常用]
平方取中法(key的平方的中间若干位作为hash值)[很少用]
除留余数法 (H(key) = key % mod)[常用][存在冲突]
解决除留余数法中冲突的方法
线性探查法(Linear Probing): [该方法容易扎堆]
H(key)+1,即冲突了就找紧挨着的下一个位置,若超过表长则从表首元素开始
平方探查法(Quadratic Probing):[避免扎堆]
H(key)+12,H(key)-12,H(key)+22,H(key)-22,H(key)+32,按该顺序检查,若超过了表长则把H(key)+k2对表长取模作为下一个探查位。若出现H(key)-k2<0的情况,加表长的n倍得到第一个正数作为下一个探查位。
链地址法(拉链法):
把所有H(key)相同的key链成一条单链表,设定一个单链表数组Link[mod],其中Link[h]存放H(key)=h的的一条单链表,如此可以对应到所有的key。
补充:前两种都找到新的hash地址,称为开放定址法。
上机一般不需要自己实现,可直接使用标准模板库的map来直接使用hash功能解决冲突。(C++11后可以用更快的unordered_map)
知识点5:字符串的hash(初级)[进阶见12.1节]
若key不为整数,比如一个二维坐标映射为一个整数,假设坐标为(x,y) 其中x≥0, y≤Range
则令H(P) = x * Range + y,可每个坐标得到唯一H(P),再通过整数hash的方法得到更小的范围。
对于字符串,先假设字符串由26个大写字母A~Z构成,把它们视作0~25,接着相当于把二十六进制转为十进制,转换成的整数最大为26len-1,其中len为字符串长度

对于有小写字母的,则把26~51代替小写字母,接着相当于五十二进制转为十进制,代码如下:


对于有数字的,52~61来代替数字,接着六十二进制转十进制
如果数字出现的有规律,比如在字符串末尾有规定个数的数字,如BCD4可先将BCD转为731,再拼接后面的数字得7314,代码如下:

综合问题:给出N个字符串(由3位大写字母组成),再给出M个查询字符串,问每个查询字符串在N个字符串中的出现次数。
#include<cstdio> const int maxn = 100; char S[maxn][5], temp[5]; int hashTable[26 * 26 * 26 + 10]; int hashFunc(char S[], int len){ //将字符串转换为整数 int id = 0; for(int i = 0; i < len; i++){ id = id * 26 + (S[i] - 'A'); } return id; } int main(){ int n, m; scanf("%d%d", &n, &m); for(int i = 0; i < n; i++){ scanf("%s", S[i]); int id = hashFunc(S[i], 3); //将字符串S[i]转为整数 hashTable[id]++; //该字符串出现次数+1 } for(int i = 0; i < m; i++){ scanf("%s", temp); int id = hashFunc(temp, 3); ///将字符串temp转为整数 printf("%d ", hashTable[id]); //输出该字符串出现次数 } return 0; }
本篇结束,下一篇是递归和贪心
加油
