Don't lost link!
list与vector不同之处在于元素的物理地址可以任意。
为保证对列表元素访问的可行性,逻辑上互为前驱和后继的元素之间,应维护某种索引关系。这种索引关系,可抽象地理解为被索引元素的位置(position),故列表元素是“循位置访问”(call-by-position)的;也可形象地理解为通往被索引元素的链接(link),故亦称作“循链接访问”(call-by-link)。这种访问方式,如同通过你的某位亲朋,找到他/她的亲朋、亲朋的亲朋、...。注意,向量中的秩同时对应于逻辑和物理次序,而位置仅对应于逻辑次序。
本章的讲解,将围绕列表结构的高效实现逐步展开,包括其ADT接口规范以及对应的算法。此外还将针对有序列表,系统地介绍排序等经典算法,并就其性能做一分析和对比。
引入list结构的目的,就在于弥补向量结构在解决某些应用问题时,在功能和性能方面的不足。二者之间的差异,表面上是体现于对外的操作方式,但根源在于其内部存储方式的不同。
数据结构支持的操作无非是静态和动态两种:静态仅从中获取信息,后者则会修改数据结构的局部甚至是整体。
静态举例:
size(); get(); //可在常数时间内完成
insert(); remove(); // 需要线性时间,原因在于各元素的物理地址连续
一、从向量到链表:
链表(list)是采用动态存储结构的典型策略;
节点(node).各节点之间通过指针或引用彼此连接,在逻辑上构成一个线性序列。
L = {a0,a1,a2,....,an-1}
相邻节点之间彼此互称为前驱(predecessor)或后继(successor)。前驱或后继若存在,则必然唯一。
没有前驱/后继的节点称为首(first/front)节点/末(last/rear)节点.

如果依然采用和向量相同的循秩访问方式,则秩越大成本越高。因此应该改用循位置访问,利用节点之间的相互引用,找到特定的节点。
二、ADT接口:
2.1 列表节点对象支持的操作接口:
1 data() 当前节点所存数据对象 2 pred() 当前节点前驱节点的位置 3 succ() 当前节点后继节点的位置 4 insertAsPred(e) 插入前驱节点,存入被引用对象e,返回新节点位置 5 insertAsSucc(e) 插入后继节点,存入被引用对象e,返回新节点位置
ListNode模板类
typedef int Rank; //秩 #define ListNodePosi(T) ListNode<T>* //列表节点位置 template <typename T> struct ListNode { //列表节点模板类(以双向链表形式实现) // 成员 T data; ListNodePosi(T) pred; ListNodePosi(T) succ; //数值、前驱、后继 // 极造函数 ListNode() {} //针对header和trailer的构造 ListNode( T e, ListNodePosi(T) p = NULL, ListNodePosi(T) s = NULL) : data(e), pred(p), succ(s) {} //默认构造器 // 操作接口 ListNodePosi(T) insertAsPred(T const& e); //紧靠当前节点之前插入新节点 ListNodePosi(T) insertAsSucc(T const& e); //紧随当前节点之后插入新节点 };
2.2 列表对象支持的操作接口:
size() //报告列表的当前闺蜜(节点总数) 列表 first()、last() //返回首、末节点的位置 列表 insertAsFirst(e) insertAsLast(e) //将e作作首、末节点插入 列表 insertBefore(p, e) insertAfter(p, e) //将e当作节点p的直接前驱、后继插入 列表 remove(p) // 删除位置p处的节点,返回其数值 列表 disordered() //判断所有节点是否已按非降序排列 列表 sort() //调整各节点的位置,使列表按非降序排列 列表 find(e) // 查找目标元素e,失败时返回NULL 列表 search(e) //查找目标元素e,返回不大于e且秩最大的节点 有序列表 deduplicate() //剔除重复节点 列表 uniquify() //剔除重复节点 有序列表 traverse() //遍历并统一处理所有节点,处理方法由函数对象指定 列表
list模板类:
1 #include "listNode.h" //引入列表节点类 2 3 template <typename T> class List { //列表模板类 4 5 private: 6 int _size; ListNodePosi(T) header; ListNodePosi(T) trailer; //规模、头哨兵、尾哨兵 7 8 protected: 9 void init(); //列表创建时的初始化 10 int clear(); //清除所有节点 11 void copyNodes(ListNodePosi(T), int); //复制列表中自位置p起的n项 12 void merge(ListNodePosi(T)&, int, List<T>&, ListNodePosi(T), int); //有序列表区间归并 13 void mergeSort(ListNodePosi(T)&, int); //对从p开始连续的n个节点归并排序 14 void selectionSort(ListNodePosi(T), int); //对从p开始连续的n个节点选择排序 15 void insertionSort(ListNodePosi(T), int); //对从p开始连续的n个节点插入排序 16 17 public: 18 // 极造函数 19 List() { init(); } //默认 20 List(List<T> const& L); //整体复制列表L 21 List(List<T> const& L, Rank r, int n); //复制列表L中自第r项的n项 22 List(ListNodePosi(T) p, int n); //复制列表中自位置p起的n项 ’23 // 析构函数 24 ~List(); //释放(包含头、尾哨兵在内的)所有节点 25 // 只读访问接口 26 Rank size() const { return _size; } //规模 27 bool empty() const { return _size <= 0; } //判空 28 T& operator[](Rank r) const; //重载,支持循秩访问(效率低) 29 ListNodePosi(T) first() const { return header->succ; } //首节点位置 30 ListNodePosi(T) last() const { return trailer->pred; } //末节点位置 31 bool valid(ListNodePosi(T) p) //判断位置p是否对外合法 32 { return p && (trailer != p) && (header != p); } //将头、尾节点等同于NULL 33 int disordered() const; //判断列表是否已排序 34 ListNodePosi(T) find(T const& e) const //无序列表查找 35 { return find(e, _size, trailer); } 36 ListNodePosi(T) find(T const& e, int n, ListNodePosi(T) p) const; //无序区间查找 37 ListNodePosi(T) search(T const& e) const //有序列表查找 38 { return search(e, _size, trailer); } 39 ListNodePosi(T) search(T const& e, int n, ListNodePosi(T) p) const; //有序区间查找 40 ListNodePosi(T) selectMax(ListNodePosi(T) p, int n); //在p及其前n-1个后继中选出最大者 41 ListNodePosi(T) selectMax() { return selectMax(header->succ, _size); } //整体最大者 42 // 可写访问接口 43 ListNodePosi(T) insertAsFirst(T const& e); //将e当作首节点插入 44 ListNodePosi(T) insertAsLast(T const& e); //将e当作末节点插入 45 ListNodePosi(T) insertBefore(ListNodePosi(T) p, T const& e); //将e当作p的前驱插入 46 ListNodePosi(T) insertAfter(ListNodePosi(T) p, T const& e); //将e当作p的后继插入 47 T remove(ListNodePosi(T) p); //初除合法位置p处的节点,返回被删除节点 48 void merge(List<T>& L) { merge(first(), size, L, L.first(), L._size); } //全列表归并 49 void sort(ListNodePosi(T) p, int n); //列表区间排序 50 void sort() { sort(first(), _size); } //列表整体排序 51 int deduplicate(); //无序去重 52 int uniquify(); //有序去重 53 void reverse(); //前后倒置(习题) 54 // 遍历 55 void traverse(void (*)(T&)); //遍历,依次实施visit操作(函数指针,只读或局部性修改) 56 template <typename VST> //操作器 57 void traverse(VST&); //遍历,依次实施visit操作(函数对象,可全局性修改) 58 }; //List
三、无序列表

头节点和尾节点经过封装之后,是对外部不可见的,但是却非常有用。设置header和trailer后,first()和last()操作就可以转换为header->succ和trailer->pred。哨兵节点的引入,也使得各种算法不需要对边界退化情况做专门的处理。
等效的头、首、末、尾节点的秩可分别理解为-1,0,n-1,n
3.1构造
列表的构造即先创建一对头、尾哨兵节点,并适当设置其前驱和后继指针,构成一个双向链表。

3.2列表的循秩访问

其时间复杂度为 O(n)
3.3 查找

最坏复杂度是O(n),线性正比于查找区间的宽度。
下图分别代表的是在p的n个前驱中查找元素e;在p的n个后继中查找元素e。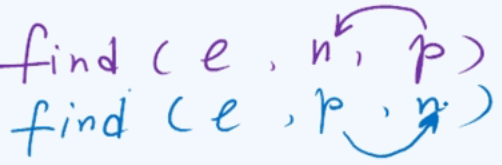
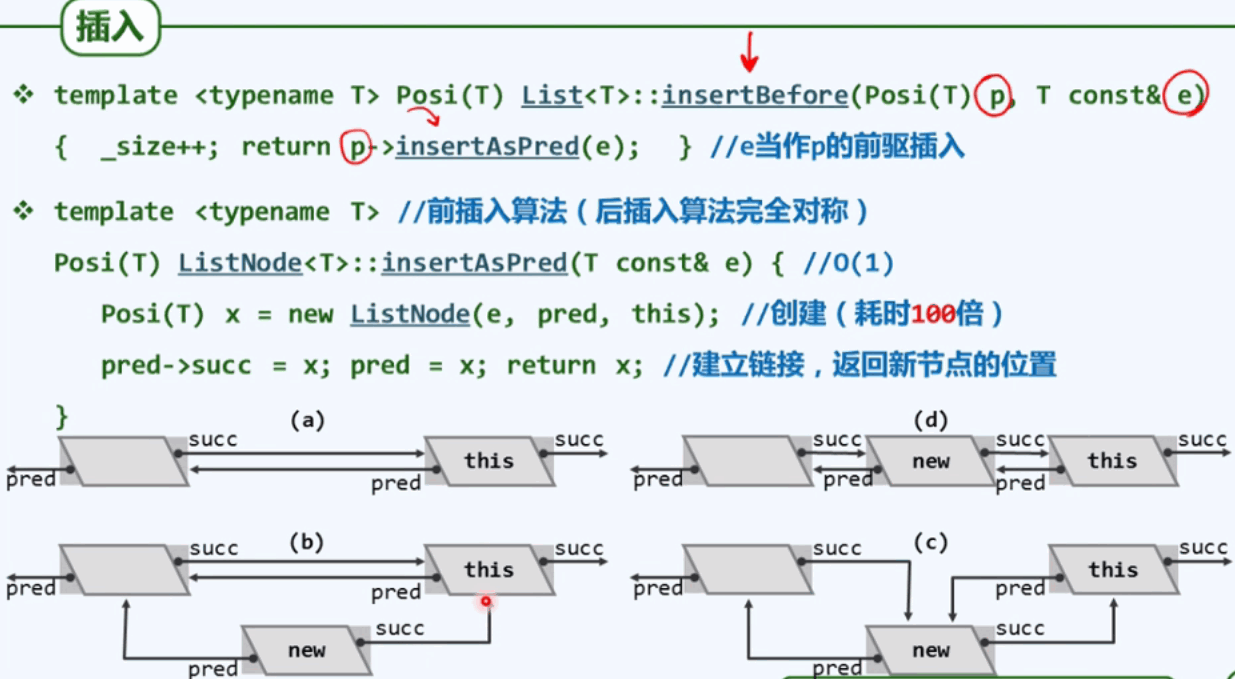
3.3 插入
微创手术:复杂度是常数。下图中的pred = x实质上是把当前节点的前驱之指向x; 如果pred->succ = x,pred =x;改为pred =x;pred->succ = x;是错误的,因为pred =x;先将当前this节点的前驱变为x,则pred->succ,就是x->succ再指向x自己。
3.4 基于复制的构造

从原列表中取出n个相邻的节点,并逐一作为末节点插入新列表中。 insertAsLast() 就相当于insertAsPred(trailer)。
3.5 删除
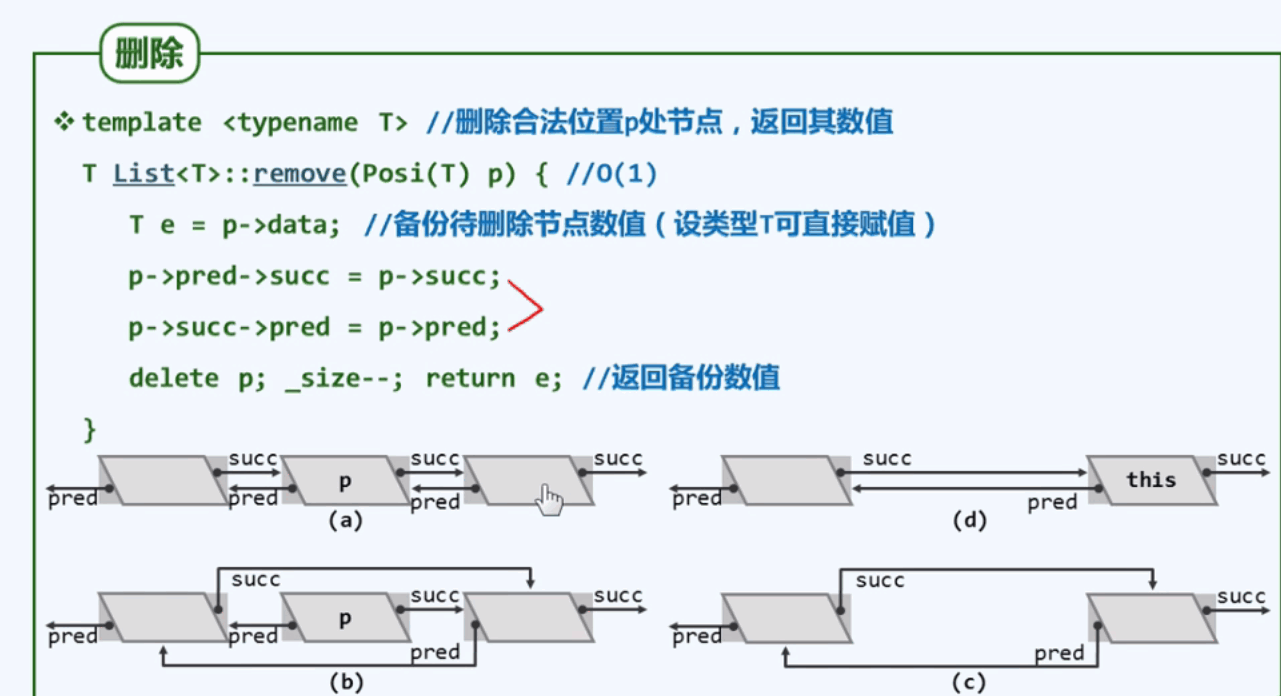
3.6 析构
- 将对外可见节点逐一删除
- 删除两个哨兵
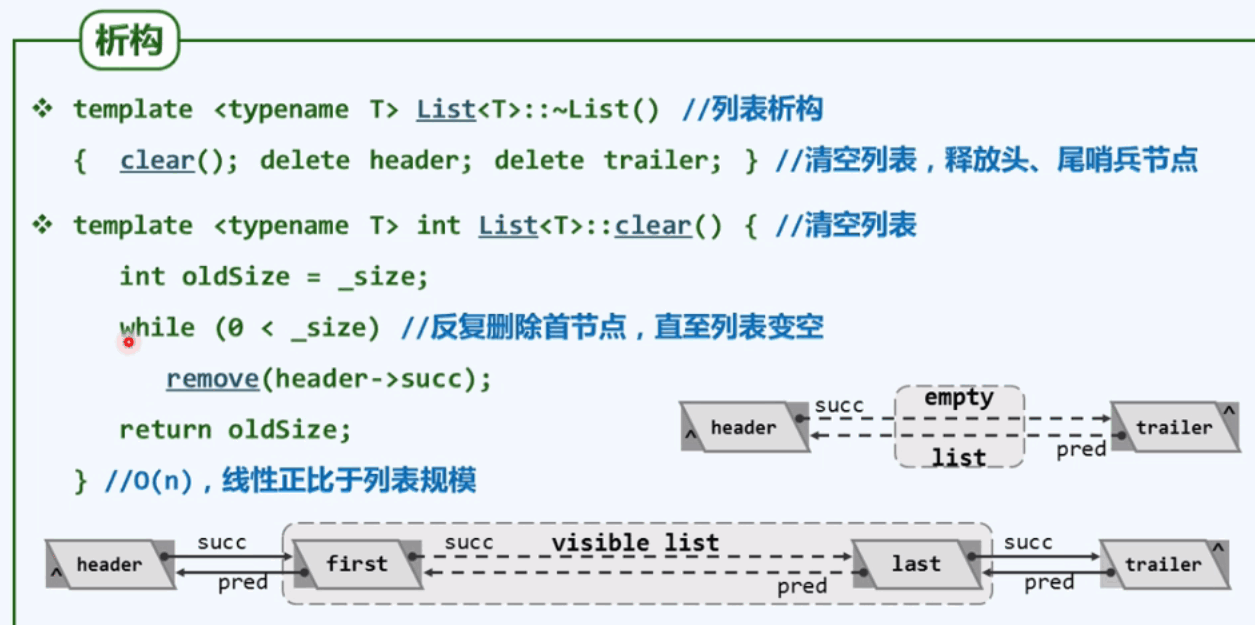
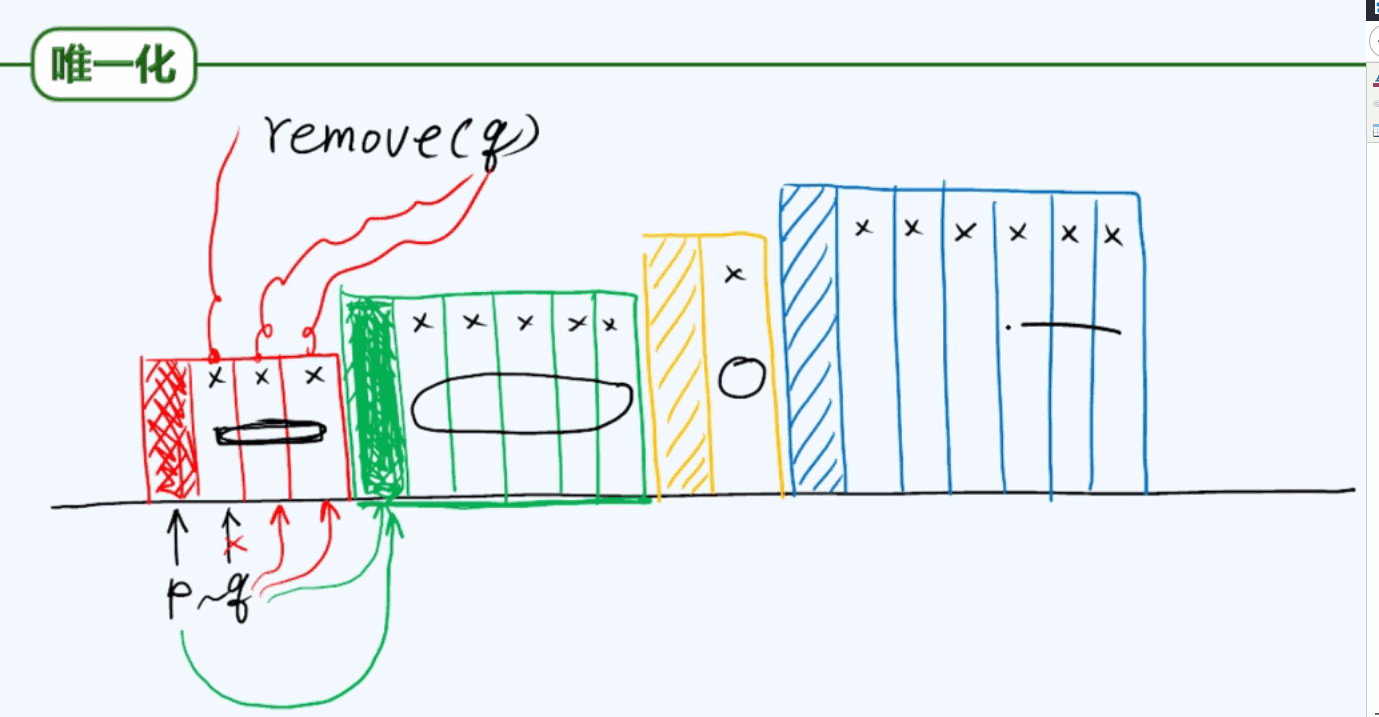
3.7 唯一化

四、有序列表
4.1 有序列表唯一化:

4.1 查找:
· 