示例:
1.夜间门诊
2.多任务操作系统
3.Huffman编码
A 问题模式: 循优先级访问(call by priority), 按照这种优先级通过调度器将最高优先级的元素输入给服务端。
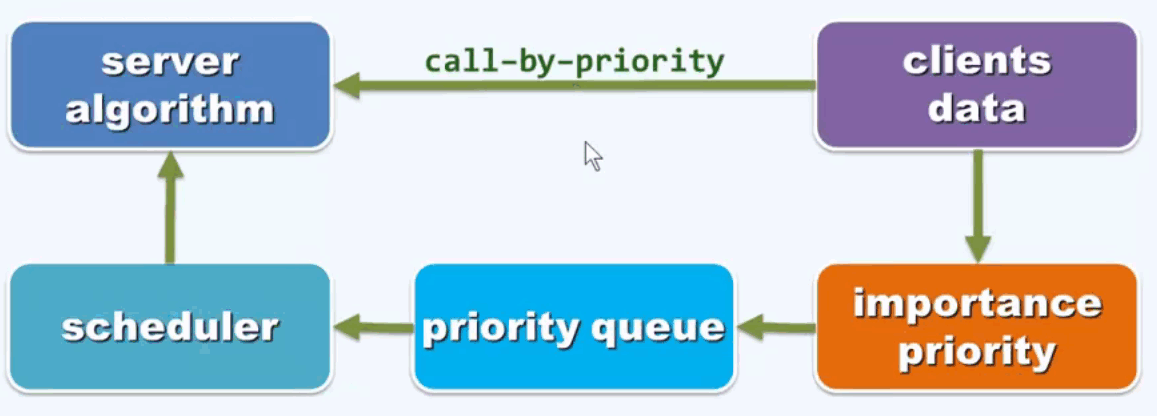
B 操作接口:
template <typename T>struct PQ {
virtual void insert(T) = 0; //按照优先级次序插入词条
virtual T getMax() = 0 ; //取出优先级最高的词条
virtual T delMax() = 0; //删除优先级最高的词条
};
Stack和Queue,都是PQ的特例——其优先级完全取决于元素的插入次序。对于栈而言,越是晚到的元素,其优先级越高,更早的出栈被处理。而队列相反。
C 实现尝试:
efficiency and cost
C1 实现为Vector: 将每个新加入的元素放在向量的末尾。
插入的时间成本:O(1) 获得元素值的时间成本是:O(n) 删除元素的时间成本是: O(n)
C2 实现为Sorted Vector: 即优先级最大的元素放入向量的末尾。
插入的时间成本:O(n) 获得元素值的时间成本是:O(1) 删除元素的时间成本是: O(1)
C3 实现为List:
插入的时间成本:O(1) 获得元素值的时间成本是:O(n) 删除元素的时间成本是: O(n)
C4 实现为Sorted List:
插入的时间成本:O(n) 获得元素值的时间成本是:O(1) 删除元素的时间成本是: O(1)
C5 实现为BBST: AVL Splay Red-black 杀鸡用了牛刀
PQ = 1 x insert() + 0.5 x search() + 0.5 x remove() = 2/3 x BBST
若只需要查找极值元素,则不必维护所有元素之间的全序关系,偏序足以。找一种实现简单、维护成本更低的实现方式。
D最终尝试: 完全二叉堆
以向量为形,以树形结构为神,完全二叉树
逻辑上,等同于完全二叉树。物理上,直接借助向量实现。
逻辑节点与物理元素依层次遍历次序彼此对应:
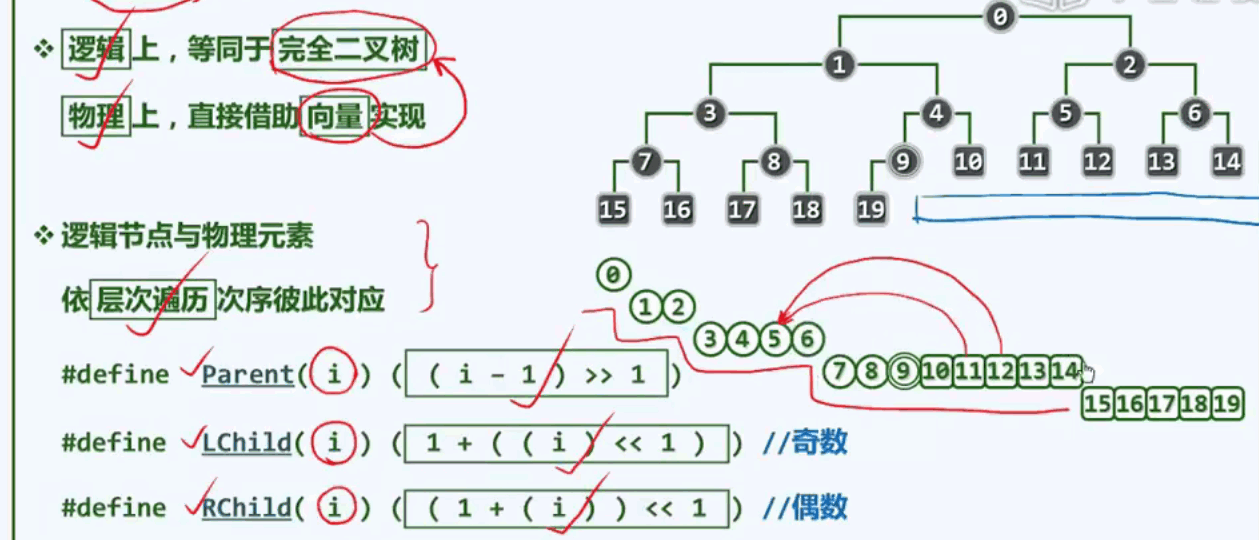
完全二叉堆实现:
template <typename T> class PQ_ComplHeap : pubilc PQ<T>, public Vector<T> {
protected:
Rank percolateDown(Rank n, Rank i); //下滤
Rank percolateUp(Rank i); //上滤
void heapify(Rank n); //Floyd 建堆方法
public:
PQ_ComplHeap(T* A, Rank n) {//批量构造
copyForm(A,0,n); heapify(n); }
void insert(T); //按照比较器确定的优先次序,插入词条
T getMax() {return _elem[0] ; } //读取优先级最高的词条
T delMax(); //删除优先级最高的词条
};
堆序性:
H[i] <= H[Parent(i)] : 任何一个节点在数值上都不会超过它的父亲。所以根据优先级队列的特性,最大元必然位于根节点位置。所以H[0]是全局最大元素。
template <typename T> T
PQ_Complate<T> :: getMax() {return _elem[0];}
E完全二叉堆插入(上滤操作):
E1:算法
为插入词条e,只需要将e作为末元素接入向量:1.结构性自然保持。2.若堆序性也被破坏,则完成。否则只能是e与其父节点违反堆序性,则只需要将e与其父节点互换位置即可。

如果交换后,仍然违反逆序性,则只需要将e与新的父节点互换位置即可。如此反复交换的过程满足单调性。这一过程即所谓的上滤过程。
而一旦过程终止,则堆序性在整个完全二叉堆中得到了完全的恢复。
E2实例:

E3实现:

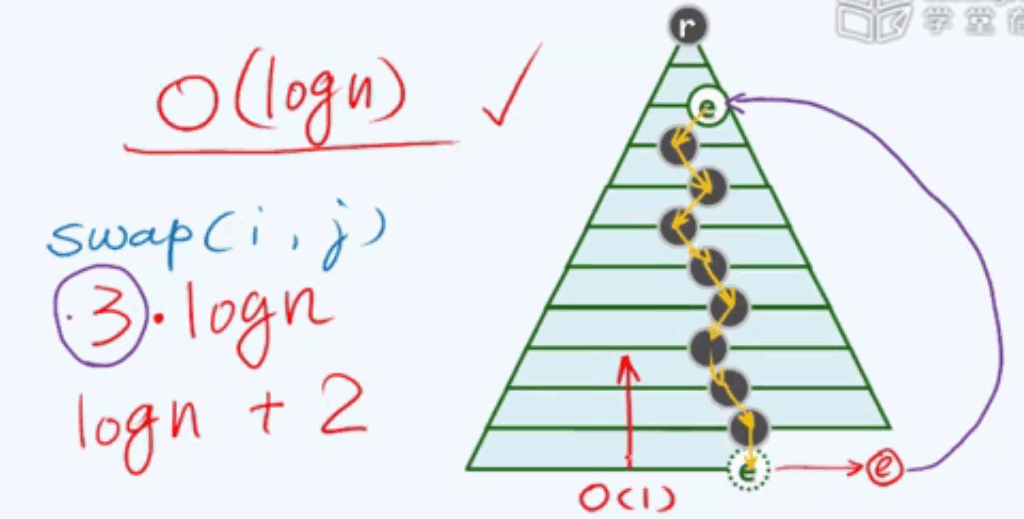
E4效率:
O(logn),但其中swap操作包含3次赋值操作。所以效率为3*logn.
所以当新插入节点与其父节点需要交换时,我们只需将新插入词条e先备份,然后将其不断上移,最后与其父亲交换。
F完全二叉堆删除:
F1:算法
最大元素始终在堆顶,所以我们只需将其摘除。
在摘除之后,完全二叉堆的堆序性被破坏,此时我们先将末尾元素放置于堆顶。
最后采用下滤操作:
1)e与孩子中的大者互换,若堆序性完成,则结束。
2)否则e与孩子中的最大者继续交换,若堆序性完成,则结束。

F2:实例

F3:实现

F4:效率
其效率与树的高度O(h)具有关系,所以其时间复杂度应为3* O(logn),同样在这里,常数项系数可以得到改进,可以先保存根节点,然后再下滤,最终只做一次实质上的交换操作(3次赋值)
在上滤过程中,新插入的节点e只需要与其父节点进行比价。在下滤过程中,根节点要与其孩子做两次比较。这在二叉堆中并不至关重要,但是在多叉堆中就至关重要。
G完全二叉堆批量建堆:
G1:算法
对于任给的n个元素,我们希望将它们构建成一个堆,这样一个过程称之为heapification
G2:自上而下的上滤实现
PQ_ComplHeap(T*A, Rank n) {copyFrom(A,0,n); heapify(n);}
template <typename T> void PQ_ComplHeap<T>: heapify(Rank n) {
for (int i =1; i < n; ++i) //按层次遍历次序逐一
percolateUp(i); //经过上滤插入各个节点
}
G3:自上而下的上滤的效率
最坏情况下,即每个节点都需要上滤至根节点,所需成本线性正比于其深度。即便只考虑最底层(n/2个节点),深度均为O(logn),累计耗时O(nlogn),但是这么长的时间消耗足以全排序。
G4:自下而上的下滤实现
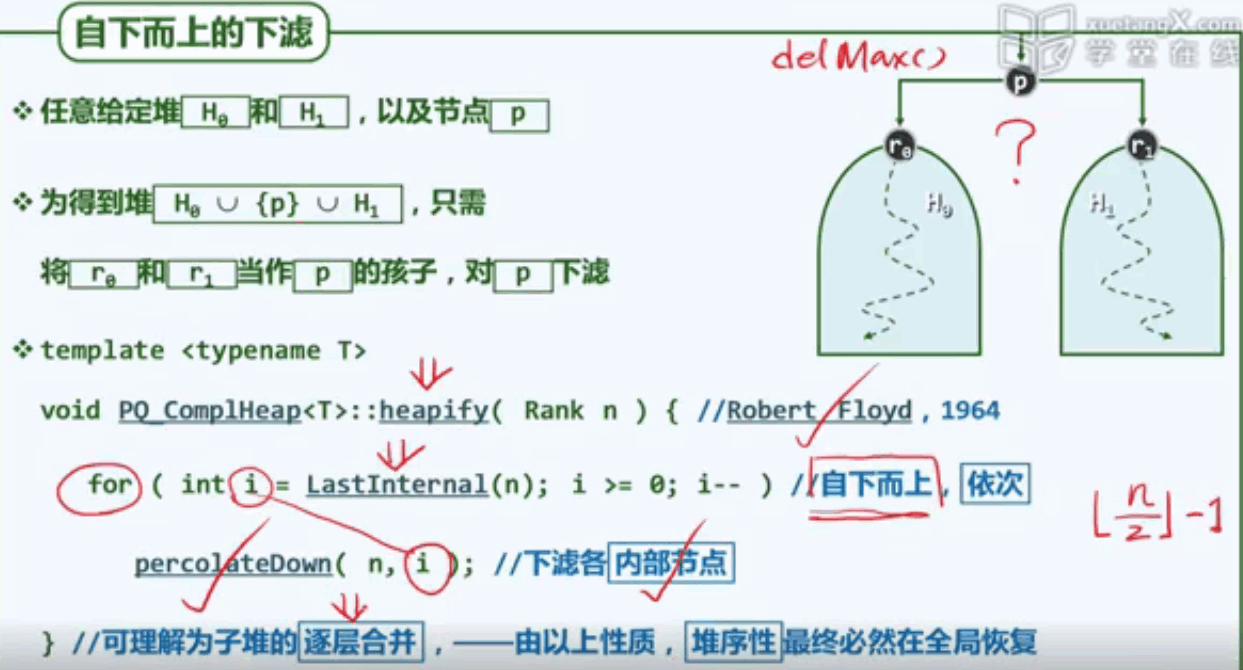
G5:自下而上的下滤实例

G6:自下而上的下滤效率:
最坏情况下,每个内部节点所需的调度时间,正比于其高度而非深度。高度是从下往上数。而深度与高度相反,从上往下数。
对每个节点的高度求和,为O(n). 可以接受
对每个节点的深度求和,为O(nlogn). 不可以接受
为什么会出现这种情况呢?因为深度是从上往下数的,而一个完全二叉堆,其处于下部的节点数较多,所以其累计的总和就更大。而以高度作为计算,位于完全二叉堆上部的节点较少,所以其累计的总和较少。
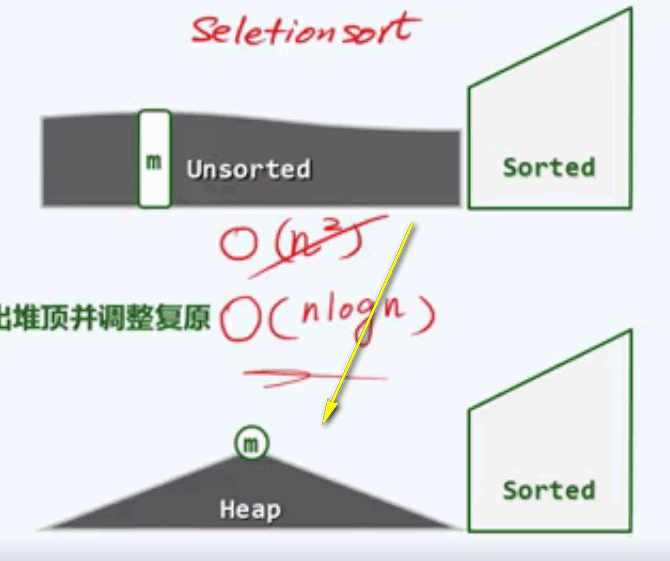
H堆排序:
还记得选择排序嘛!
我们始终将整个序列分为两部分:一部分是已经排好序的部分,另一部分是待排序部分。所以我们反复遍历待排序部分的最大值,O(n2)
H1使用完全二叉堆来替代原有的待排序部分:
在此,我们使用完全二叉堆,来替代原有的待排序部分。
初始化:heapify(),O(n),建堆
迭代:delMax(),O(logn),取出堆顶并调整复原
不变性:H <= S
H2在向量内完成堆排序:
已排序的部分构成向量的后端,而与之互补的前缀恰好构成一个完全二叉堆,堆中的最大元必然是0号元素,而接下来与之兑换的x必然是已排序单元秩为-1的元素,所以我们首先取出最大的元素,然后用x取而代之。
然后将备份的最大元植入x,然后对新的根节点作下滤调整。

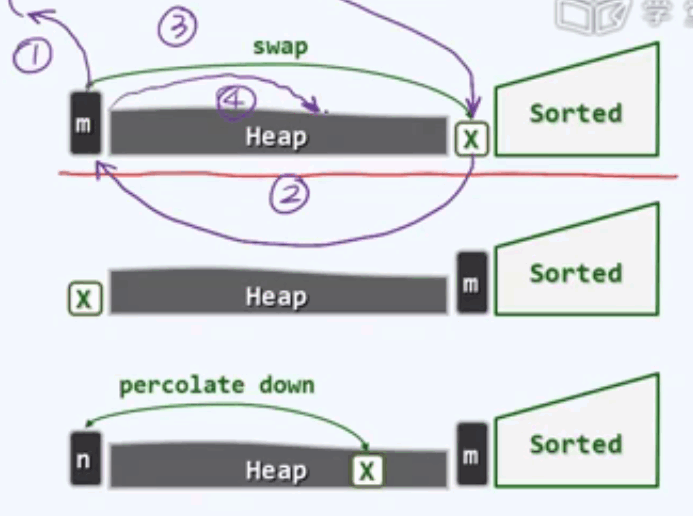
规整为两部分:交换和下滤,直至堆变空。除了交换需要常数个辅助空间外,除此我们不需要更多的辅助空间。
H2堆排序实现:

H2堆排序实例:
I左式堆:
I1堆合并:
方法1:
A.insert(B.delMax()) O(m*(logm + log(n+m))) = O(m*log(n+m))
方法2:
union(A,B).heapify(n+m) = O(m + n)
I2堆单侧倾斜:
保持堆序性,附加新条件。使得在堆合并过程中,只需要调整很少的部分节点, O(logn)
新条件 = 单侧倾斜: 节点分布偏向于左侧,合并操作只涉及右侧。
如果真的存在这样一个堆,那么它断然不再是完全二叉堆,堆序性才是其本质性要求,而结构性则不是其本质要求,所以为了效率在此牺牲其结构性。
I3空节点路径长度:从该节点到达一个没有两个孩子的节点的最短距离。NULL的NPL为-1,而左式堆的核心约束条件是左倾即任意节点的左0孩子的NPL大于等于右孩子的NPL。
npl(x) = 1 + npl(rc(x)),满足左倾性的堆,称之为左式堆 。左倾性与堆序性相容但是不矛盾。左式堆的子堆,必然是左式堆。左式堆倾向于更多节点分布于左侧分支。
引入所有的外部节点:消除一度节点,转为真二叉树
npl(x) = x到外部节点的最近距离
npl(x) = 以x为根的最大满子树的高度、
npl(Null) = 0; npl(x) = 1 + min(npl(lc(x), npl(rx(x))));
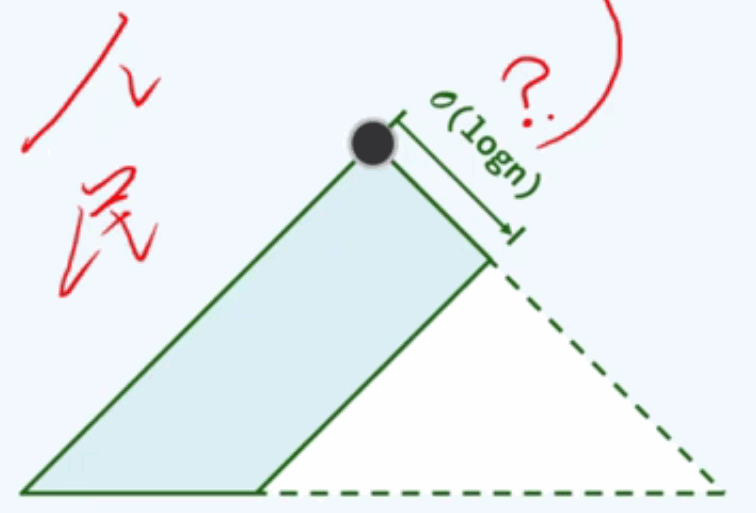
I3右侧链:
rChain(x) : 从节点x出发,向右不断前行所确立的那个分支就称之为右侧链。
rChain(root)的终点,必然是全堆中最浅的外部节点。
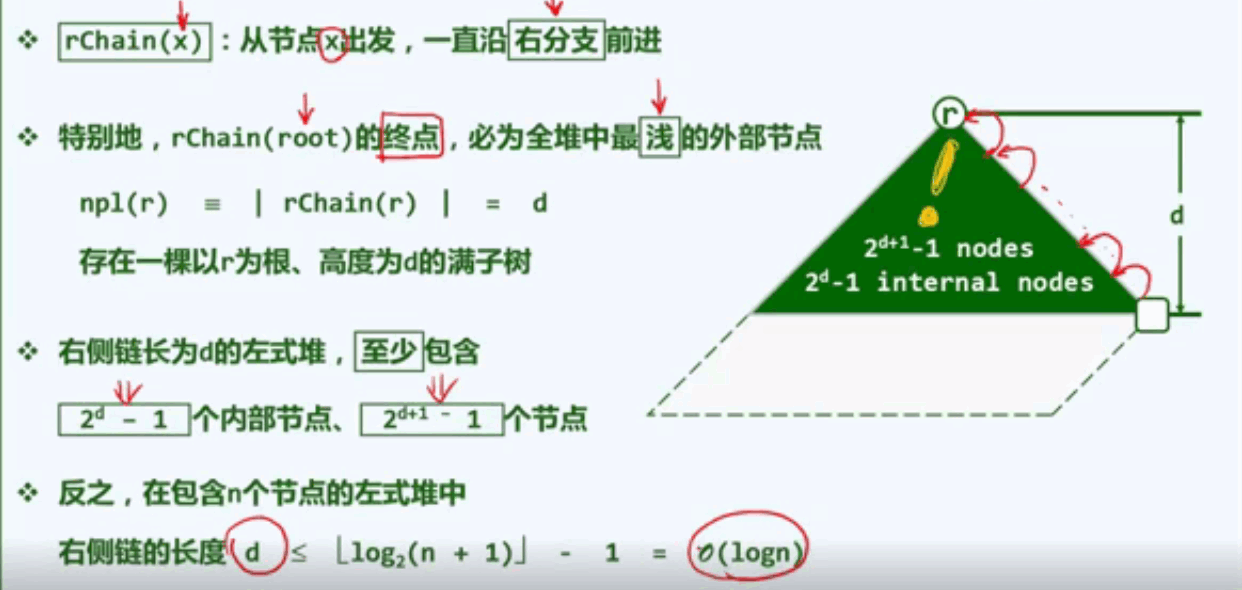

I4左式堆的合并算法:左式堆不再满足结构性,物理结构不再保持紧凑性。
 以外部形式给出合并两个左式堆的函数:
以外部形式给出合并两个左式堆的函数:

先将a的右式堆与b合并,合并所得的结果作为a的右子堆,然后比较a的左式堆和右式堆的npl值,如果比它小,则互换位置。
I5左式堆的合并算法实现:
I5左式堆的合并算法实例:
https://next.xuetangx.com/learn/THU08091002048/THU08091002048/1158035/video/784339
I5左式堆的插入算法:
插入就是合并
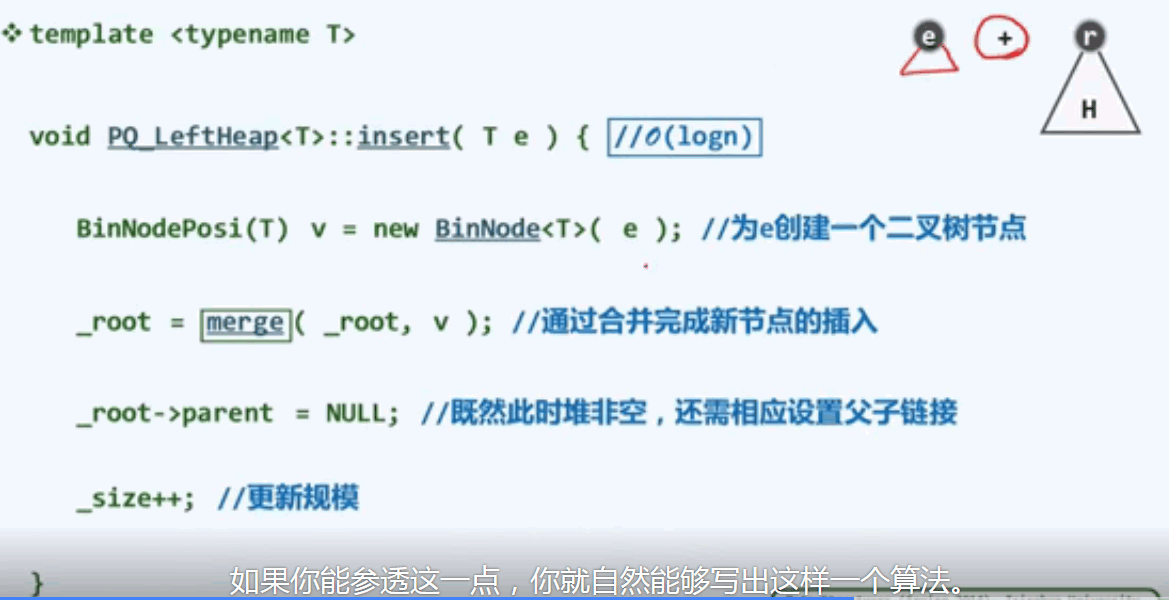
I5左式堆的删除算法:
删除也是合并
