转载自知乎
https://zhuanlan.zhihu.com/p/33117537
背景回顾
假设我们开了一家叫Surprise Me的饭馆
- 客人来了不用点餐,由算法从N道菜中选择一道菜推荐给客人
- 菜的成分可以表述为<蛋白质,维生素>
- 用户的身体状况可以表述为<蛋白质,维生素>
- 优化目标:最大化用户就餐次数
- 如果推荐的菜一直能让用户处于健康状态,则用户会保持就餐(回头率高)
- 如果推荐的菜使得用户处于亚健康状态(营养成分超标或不够),则会永远流失这个用户
- 如果连续两次推荐一样的菜,则会永远流失这个用户
如何建模成强化学习问题
步骤1 刻画用户的状态 (State): 用户的状态可以表示成<蛋白质,维生素,上次就餐的菜>
- 蛋白质正常范围为[1, 5]
- 维生素的正常范围为[1, 3]
步骤2 刻画决策空间 (Action): 我们一共有4道菜,每道菜可以看成是一个Action,因此一共有4种Action
- 菜1 = <蛋白质: 0, 维生素: 1>
- 菜2 =<蛋白质: 0, 维生素: 1> (跟菜1营养成分相同)
- 菜3 =<蛋白质: 2, 维生素: 1>
- 菜4 =<蛋白质: 2, 维生素: 1> (跟菜3营养成分相同)
步骤3 刻画Action对State的影响,i.e. P(State' | State, Action)
- 给定Action=某道菜,就餐后的State=<蛋白质 - 1 + 菜的蛋白质,维生素 - 1 + 菜的维生素,这次就餐的菜> ,-1表示从上次就餐到现在消耗了1个单位
步骤4 刻画Action带来的回报Reward,i.e. P(Reward | State, Action)
- 如果推荐的菜(Action)使得用户保持健康,且跟上次的菜不重复,则就餐次数+1,即Reward=1
- 如果推荐的菜(Action)使得用户变成亚健康状态,或者推荐了跟上次一样的菜,则用户永久离开,客户永远流失且Reward=0
步骤5 刻画优化目标 = ,如果客户流失,则Reward=0且不再会有后续的Reward。
状态 (State)、决策(Action)、马尔科夫决策过程(MDP)
从用户状态的定义可以看出,状态空间一共有三维,且每个维度都是离散取值的:
- 维生素只有3种取值:{1, 2, 3}
- 蛋白质只有5种取值:{1, 2, 3, 4, 5}
- 上一顿吃的菜只有5种取值:{null, 1, 2, 3, 4}
由上可以得出整个状态空间可以用一个3x5x4的魔方表示,如下图所示:
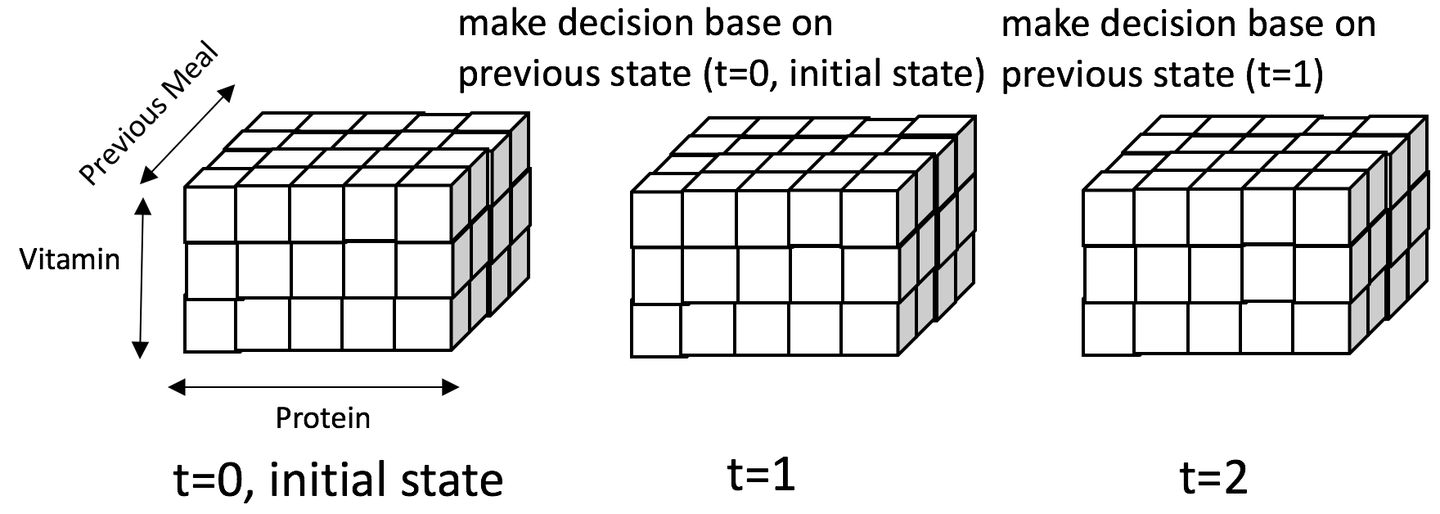
图中展示了一个客户来三次就餐情况:
- 第一次就餐 (t=0, initial state)
- 用户的初始状态为 State=(蛋白质:3, 维生素:3, 上次就餐的菜: null)
- 在这个例子中,我们推荐了菜4=(蛋白质: 2,维生素:1)
- 用户的状态变为State'=(蛋白质:4,维生素:3,上次就餐的菜: 4)
- 第二次就餐 (t=1)
- 用户的状态State=(蛋白质:4,维生素:3,上次就餐的菜: 4)
- 在这个例子中,我们推荐了菜1=(蛋白质:0, 维生素:1)
- 用户的状态变为State'=(蛋白质: 3, 维生素: 3, 上次就餐的菜: 1)
- 第三次就餐 (t=2)
- 用户的状态State=(蛋白质:3, 维生素:3, 上次就餐的菜: 1)
- 在这个例子中,我们推荐了菜4=(蛋白质: 2,维生素:1)
- 用户的状态变为State'=(蛋白质:4,维生素:3,上次就餐的菜: 4)
在这个例子中有两个重要的观察:
- 需要探索的状态空间是有限的:第三次就餐产生的状态与第一次就餐产生的状态一模一样,我们可以借用第二次就餐的成功经验来处理第四次就餐
- 马尔科夫决策过程 (MDP):Action的选取只依赖用户当前的状态,与之前的历史行为都没有关系,我们把这个决策过程称为马尔科夫决策过程(MDP)
需要注意的是一个问题满足马尔科夫性并不难:
- 极端情况下State可以是之前所有Action的集合S=(initial state, aciton1, action2, ... action_n)
- 但是,状态State随着action的增大而不断增大,需要探索的状态空间变得无限大,无论有多少训练数据,都是无法解决的。所以状态空间的有限性是至关重要的。
最后总结一下MDP问题的核心元素:
- 状态空间State:<蛋白质,维生素,上次就餐的菜>
- 本文只考虑在有限离散空间(以后考虑连续空间、无限取值的情况)
- 决策空间Action: 推荐菜1、2、3、4
- 本文只考虑有限离散取值(以后考虑连续、无穷限取值的情况)
- Action对State的影响 P(State' | State, Action)
- 本文认为(State, Action) -> State'的转换关系是已知的(以后考虑未知的情况,更加符合实际问题)
- Action带来的回报P(Reward | State, Action)
- 本文认为(State, Action) -> Reward的关系是已知的(以后考虑未知情况,更加符合实际问题)
- 初始状态 P(Initial State):一个从未光顾过餐馆的客户的营养状况是什么样的