【HAOI2012】容易题

原题：

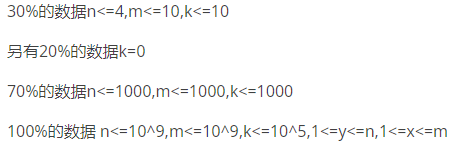
常见思路：不妨先考虑简化的问题

如果没有禁选限制怎么来做？

可以发现a1*a1+a1*a2+...+a1*ak+a2*a1+...+ak*ak=a1*(a1+a2+...+ak)+a2*(a1+...+ak)+...+ak*(a1+...+ak)=(a1+a2+...+ak)*(a1+...+ak)

接着可以想到如果前i个数的答案是f[i]，那么f[i+1]=f[i]*1+f[i]*2+...+f[i]*n=f[i]*(1+2+...+n)=f[i]*(1+n)*n/2

即如果没有禁选限制，那么最终答案就是((1+n)*n/2)^m

如果加入禁选呢，可以发现f[i+1]=f[i]*(1+n)*n/2-f[i]*b1-f[i]*b2-...f[i]*bk，其中b是不能选的数

接着就是一个既类似于离散化，又类似于DP的东西

给禁选排个序，每枚举到一个禁选，如果它和上一个禁选不位于同一个位置，那先把中间隔着的没有禁选的位置填满，即ans*=N^(ai-a_{i-1})，其中N=(1+n)*n/2，a表示禁选的位置

然后再把被禁选的位置减去，这时需要引入一个last（即DP中的f[i-1]）方便计算，当ans*=N^(ai-a_{i-1})时记录last=N^(ai-a_{i-1}-1)

然后让ans-=last*bi即可

如果当前禁选和上一禁选位于同一个位置，那么无需更新last，直接让ans-=last*bi

注意判断两个一模一样的禁止条件的情况，不要重复减了（样例很良心，包含了这种情况）

最后记得要把最后一个禁选到最后一个位置的空间补齐

确实是个容易题盒盒

代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#define LL long long
using namespace std;
const int mo=1000000007;
struct nds{LL x,y;}a[110000];
LL n,m,o;
LL qcp(LL x,LL y){
    LL bwl=1,z=x;
    for(;y;y>>=1){
        if(y&1){
            bwl=bwl*z%mo;
        }
        z=z*z%mo;
    }
    return bwl;
}
bool cmp(nds x,nds y){
    return x.x==y.x ? x.y<y.y : x.x<y.x;
}
int main(){
    scanf("%lld%lld%lld",&n,&m,&o);
    for(int i=1;i<=o;++i){
        scanf("%lld%lld",&a[i].x,&a[i].y);
    }
    sort(a+1,a+o+1,cmp);
    LL N=(1+n)*n/2%mo;
    if(o==0){
        printf("%lld
",qcp(N,m));
    }
    else{
        LL bwl=1;
        LL lst=1;
        for(int i=1;i<=o;++i){
            if(a[i].x!=a[i-1].x){
                lst=bwl*qcp(N,a[i].x-a[i-1].x-1)%mo;
                bwl=bwl*qcp(N,a[i].x-a[i-1].x)%mo;
                //cout<<bwl<<" "<<lst<<endl;
                bwl=(bwl-lst*a[i].y)%mo;
            }
            else if(a[i].y!=a[i-1].y){
                bwl=(bwl-lst*a[i].y)%mo;
            }
            //cout<<bwl<<' '<<lst<<' '<<a[i].x<<' '<<a[i].y<<endl;
        }
        bwl=bwl*qcp(N,m-a[o].x)%mo;
        printf("%lld
",(bwl+mo)%mo);
    }
    return 0;
}