感知器算法是一种可以直接得到线性判别函数的线性分类方法,由于它是基于样本线性可分的要求下使用的,所以先来了解下什么是线性可分?
- 线性可分与线性不可分
假设有一个包含 个样本的样本集合
, 其中
. 我们想要找到一个线性判别函数
将两类样本分开,其中 ,如图1所示:
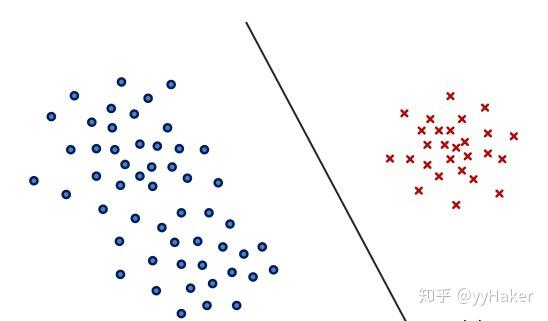 图 1
图 1
为了讨论方便,我们将样本 增加了一维常数,得到增广样本向量
,则
个样本的集合表示为
,增广权矢量表示为
,我们得到新的判别函数
对应的决策规则就变为: ,则决策为第一类;
决策为第二类.
那什么是线性可分?什么是线性不可分?
假设有一组样本 ,如果存在这样一个权矢量
,使得任何一个样本满足“属于第一类,
;属于第二类,
”这样一个条件,那么我们就说这一组样本是线性可分的,即在样本特征空间中,至少会存在一个决策面可以将两类样本正确无误的分开,反之找不到一个决策面来区分的话,就说样本是线性不可分的。
对于感知器,我们要求样本必须是线性可分的,因为它作为一种最最简单的学习机器,目前还无法很好的解决线性不可分的情况(当然,有了解决不可分的算法),即便是不可分的情况,人们也更加倾向于使用其他算法,这也是感知器无法应用到更多实践场合的原因。
2. 感知器算法
感知器算法采用最直观的准则,即最小错分样本数。将错分样本到判别界面距离之和作为准则,称为感知器准则,表示如下:
为了求解感知器的准则函数,就是找到一个权矢量,使得惩罚函数最小化。我们使用机器学习中常用的梯度下降方法来迭代。惩罚函数对权矢量的梯度公式为:
利用梯度下降,我们有:
其中 是学习率(或步长)。
我们得到下列感知器算法(批量调整版本):

当然,我们都知道这种对所有错分样本放到一起进行修正的做法是不妥当的,更妥当的办法是对每一个错分样本都单独修正,且每次都使用同一个固定步长,假如设步长为1,得到单样本调整版本的感知器算法:

感知器算法特点:
- 当样本线性可分情况下,学习率
合适时,算法具有收敛性
- 收敛速度较慢
- 当样本线性不可分情况下,算法不收敛,且无法判断样本是否线性可分
感知器算法的原理:
感知器作为人工神经网络中最基本的单元,有多个输入和一个输出组成。虽然我们的目的是学习很多神经单元互连的网络,但是我们还是需要先对单个的神经单元进行研究。
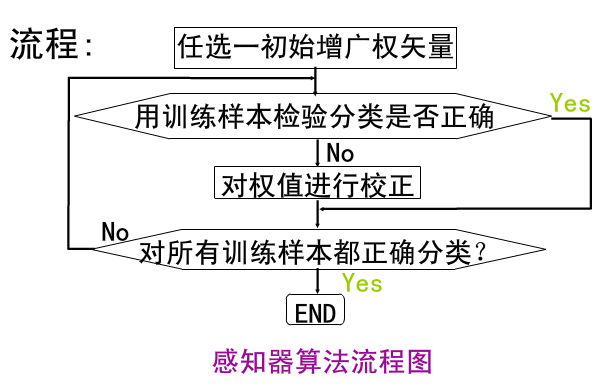
感知器算法的主要流程:
首先得到n个输入,再将每个输入值加权,然后判断感知器输入的加权和最否达到某一阀值v,若达到,则通过sign函数输出1,否则输出-1。

为了统一表达式,我们将上面的阀值v设为-w0,新增变量x0=1,这样就可以使用w0x0+w1x1+w2x2+…+wnxn>0来代替上面的w1x1+w2x2+…+wnxn>v。于是有: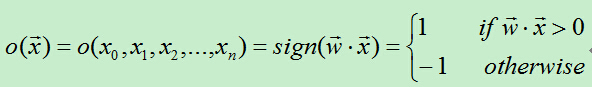
从上面的公式可知,当权值向量确定时,就可以利用感知器来做分类。
那么我们如何获得感知器的权值呢?这需要根据训练集是否可分来采用不同的方法:
1、训练集线性可分时 --> 感知器训练法则
为了得到可接受的权值,通常从随机的权值开始,然后利用训练集反复训练权值,最后得到能够正确分类所有样例的权向量。
具体算法过程如下:
A)初始化权向量w=(w0,w1,…,wn),将权向量的每个值赋一个随机值。
B)对于每个训练样例,首先计算其预测输出:
C)当预测值不等于真实值时则利用如下公式修改权向量: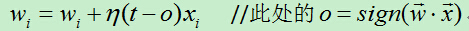
 代表学习速率,t代表样例的目标输出,o代表感知器输出。
代表学习速率,t代表样例的目标输出,o代表感知器输出。
D)重复B)和C),直到训练集中没有被错分的样例。
算法分析:
若某个样例被错分了,假如目标输出t为-1,结果感知器o输出为1,此时为了让感知器输出-1,需要将wx减小以输出-1,而在x的值不变的情况下只能减小w的值,这时通过在原来w后面添加(t-o)x=即可减小w的值(t-o<0, x>0)。
通过逐步调整w的值,最终感知器将会收敛到能够将所有训练集正确分类的程度,但前提条件是训练集线性可分。若训练集线性不可分,则上述过程不会收敛,将无限循环下去。
感知器学习算法首先需要将权重设置为0或很小的随机数,然后预测训练样本的类型。感知器是一种错误驱动(error-driven)的学习算法。如果感知器是正确的,算法就继续处理下一个样本。如果感知器是错误的,算法就更新权重,重新预测。权重的更新规则如下:
对每个训练样本来说,每个解释变量的参数值增加,是样本 j 的真实类型,是样本 j 的预测类型,是第 i 个样本 j 的解释变量的值,是控制学习速率的超参数。如果预测是正确的,等于0,也是0,此时,权重不更新。如预测是错误的,权重会按照学习速率与解释变量值的乘积增加。
这里的更新规则与梯度下降法中的权重更新规则类似,都是朝着使样本得到正确分类更新,且更新的幅度是由学习速率控制的。每遍历一次训练样本称为完成了一世代(epoch)。如果学习完一世代后,所有的样本都分类正确,那么算法就会收敛(converge)。学习算法不能保证收敛;后面的章节,我们会介绍线性不可分数据集,是不可能收敛的。因此,学习算法还需要一个超参数,在算法终止前需要更新的最大世代数。
2. 感知器算法的实现
我是用Java语言来编写的,实现的比较简单的两类,两特征的感知器算法。该算法的目的是为了计算权向量W。程序开始时输入样本数N,然后程序随机产生N个样本值。
根据感知器算法的过程,程序在进行了15次计算后得到了最终的权向量W=(10,-2,-12)。所以线性分类判别函数是10x-2y-12=0,化简得y=5x-6。为验证该函数是否能正确分类,故把所有的样本值点在XOY平面标出来,并画出y=5x-6的函数图象,结果如下所示:
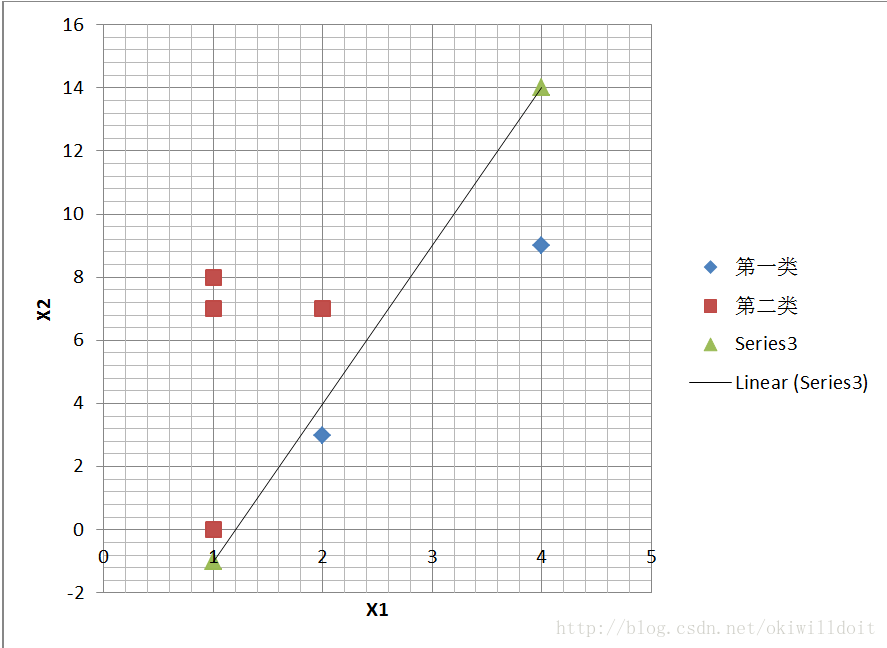
从上图中可以看出,该判别函数很好地把两类数据分开了,得到的结果还是比较准确
下面的散点图表面这些样本是可以线性分离的:
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def perception(W, w1, w2):
flag = False
while flag != True:
for i in range(len(w1)):
t1 = 0
t2 = 0
for j in range(len(W)):
t1 += W[j] * w1[i][j]
t2 += W[j] * w2[i][j]
if(t1 <= 0):
for j in range(len(W)):
W[j] += w1[i][j]
flag = False
break
if(t2 >= 0):
for j in range(len(W)):
W[j] -= w2[i][j]
flag = False
break
flag = True
print("判别函数:" + "d(x)= %d" % (W[0]) + "x" + "%d" % (W[1]) + "y" + "%d" % (W[2]) + "z+" + "%d" % (W[3]))
return W
if __name__ == '__main__':
W = [-1, -2, -2, 0]
w1 = [[0, 0, 0, 1], [1, 0, 0, 1], [1, 0, 1, 1], [1, 1, 0, 1]]
w2 = [[0, 0, 1, 1], [0, 1, 1, 1], [0, 1, 0, 1], [1, 1, 1, 1]]
W = perception(W, w1, w2)
fig = plt.figure()
ax = Axes3D(fig)
for i in range(len(w1)):
ax.scatter(w1[i][0],w1[i][1],w1[i][2],c = 'r',marker='*')
ax.scatter(w2[i][0],w2[i][1],w2[i][2],c = 'b',marker='o')
plt.grid()
xmin = min(min(w1[:][0]), min(w2[:][0]))
xmax = max(max(w1[:][0]), max(w2[:][0]))
ymin = min(min(w1[:][1]), min(w2[:][1]))
ymax = max(max(w1[:][1]), max(w2[:][1]))
x = np.linspace(xmin, xmax, 10)
y = np.linspace(ymin, ymax, 10)
x, y = np.meshgrid(x, y)
z = []
for i in range(len(x)):
z.append(((W[0]*x[i] + W[1]*y[i] + W[3]) / (-W[2])))
ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap='rainbow')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.show()