【Luogu】P3327约数个数和（莫比乌斯反演+神奇数论公式）

　　题目链接

　　真TM是神奇数论公式。

　　注明：如无特殊说明我们的除法都是整数除法，向下取整的那种。

　　首先有个定理叫$d(ij)=sumlimits_{i|n}{}sumlimits_{j|m}{}(gcd(i,j)==1)$

　　证明……我不会证qwq，可以看这个链接

　　所以原式$sumlimits_{i=1}{n}sumlimits_{j=1}{m}d(ij)$

　　　　　　=$sumlimits_{i=1}^{n}sumlimits_{j=1}^{m}sumlimits_{k=1}^{i}sumlimits_{l=1}^{j}[gcd(k,l)==1]$

　　　　　　=$sumlimits_{i=1}^{n}sumlimits_{j=1}^{m}frac{n}{i}frac{m}{j}[gcd(i,j)==1]$

　　等等这个等号是怎么推过来的？题解一笔带过，然而我死活没看懂，于是请教rqy……

　　以下是rqy的解析。

　　$sumlimits_{i=1}^{n}sumlimits_{j=1}^{m}sumlimits_{k=1}^{i}sumlimits_{l=1}^{j}[gcd(k,l)==1]$

　　=$sumlimits_{a=1}^{n}sumlimits_{b=1}^{m}[gcd(a,b)==1]sumlimits_{a|i}^{1<=i<=n}      sumlimits_{b|j}^{1<=j<=m}1$

　　=$sumlimits_{a=1}^{n}sumlimits_{b=1}^{m}[gcd(a,b)==1]frac{n}{a}frac{m}{b}$

　　然后把a统统替换成i，把b统统替换成j

　　就证明完毕啦

　　然后我们有了这个东西有什么用呢？

　　emm公式打不出来了……看Night_Aurora的题解……

　　

设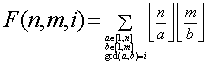

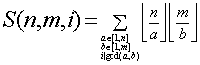
那么可发现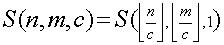

所以下文对于FS函数若第三项省略则表示第三项为1

根据莫比乌斯反演

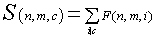
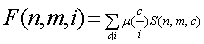
那么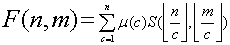

那么答案就是F(N,M)了

最后只差O(1)处理S函数了

我们再设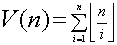

我们发现S(n,m)=V(n)*V(m)

那么我们只要开始用O(N)打一个μ的前缀和

再用O(N^1.5)试除法求出前50000个V函数的表

再对每组询问进行试除法

总复杂度是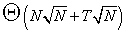

　　贴上我的代码

　　

#include<cstdio>
#include<cstring>
#include<cctype>
#include<algorithm>
#include<cstdlib>
#define maxn 50060
using namespace std;

inline long long read(){
    long long num=0,f=1;
    char ch=getchar();
    while(!isdigit(ch)){
        if(ch=='-')    f=-1;
        ch=getchar();
    }
    while(isdigit(ch)){
        num=num*10+ch-'0';
        ch=getchar();
    }
    return num*f;
}

bool s[maxn];
int prime[maxn],tot;
int miu[maxn];
long long v[maxn];

int main(){
    miu[1]=1;
    for(int i=2;i<=maxn;++i){
        if(!s[i]){
            prime[++tot]=i;
            miu[i]=-1;
        }
        for(int j=1;j<=tot&&prime[j]*i<=maxn;++j){
            s[i*prime[j]]=1;
            if(!(i%prime[j]))    break;
            miu[i*prime[j]]=-miu[i];
        }
    }
    for(int i=1;i<=maxn;++i)    miu[i]+=miu[i-1];
    for(int n=1;n<=maxn;++n){
        int x=1;
        while(x<=n){
            int y=n/(n/x);
            v[n]+=(y-x+1)*(n/x);
            x=y+1;
        }
    }
    int T=read();
    while(T--){
        int n=read(),m=read();    long long ans=0;
        int x=1,top=min(n,m);
        while(x<=top){
            int y=min(n/(n/x),m/(m/x));
            ans+=(long long)(v[n/y]*(long long)v[m/y])*(long long)(miu[y]-miu[x-1]);
            x=y+1;
        }
        printf("%lld
",ans);
    }
    return 0;
}

　　这篇博客……勉勉强强算是写（抄）完了吧……