------OGRE Camera简介
“伟大航路,我把世界上的一切都放在了那里,有种的话就去领取吧”
这是OGRE中文网的一则广告,我想,无论作为OGRE的学习者还是漫漫人生的一名旅人,这句话都是非常不错的激励语。放在这,是否能够让你隐约看到属于自己的新世界?
前言
相机的概念,在三维里面是举足轻重的,在一个个三维场景中,看着无数的人物、动画,我想无数的三维开发者在浏览三维时,脑海中都会浮现出一款属于自己的相机吧,在不停的移动,如同狗仔队那般专业的相机,耳边还回荡着成龙的那句“感动常在”。可惜我没有银子,所以只能拥有一颗单反的心而已了。
相机在三维里面属于不可或缺的成分,在红宝书里放在第三章,就彰显了其重要性。公司开发的三维GIS软件,一上来就是一个地球展现在你的眼前,依照惯性自传,吸引着我的眼球,怀着憧憬和疑问,花了两天的时间研究公司的相关代码,但是也赞叹这套相机和相机的实现确实在架构上很工整,在实现上也把复杂问题模块化,简化了问题,本来涉及到公司代码,不方便多讲,但在学习OGRE之后,发现原来公司就是移植OGRE里面的相机实现(当然在上面涉及地球GIS部分有一些接口扩展),于是针对OGRE的实现,在此总结如下吧。
视图概念
在OpenGL视图中,参考现实生活中使用照相机拍照的原理,定义了在计算机中的视图概念。在OpenGL中的照相机类比法很清晰的抽象出四个概念:视图、模型、投影、视口。
图1:照相机比喻
如上图所示,OpenGL通过相机,经过模型转换、投影转换,将物体映射到了viewport中,而在程序步骤中,也吻合如上的使用方式。
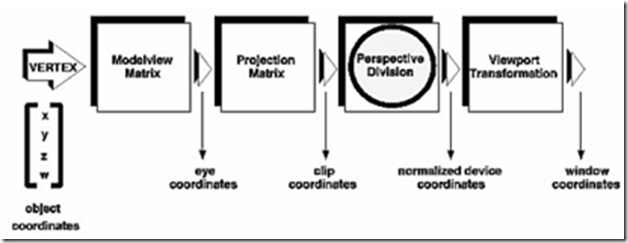
图2:转换流程
上面的四个过程简单如下:
l 模型数据获取
获取实物的顶点数组和索引数组信息
l 视图矩阵转换
根据视图相机的成像原理,转换成对应的视图矩阵,主要负责物体在视口中的现实位置和角度
glMatrixMode(GL_MODELVIEW);
glLoadMatrixf(mat);
l 投影矩阵转换
投影矩阵主要负责裁剪,实现物体在视口中的显示部分的裁剪
glMatrixMode(GL_PROJECTION);
glLoadMatrixf(mat);
l 显示
OpenGL在设置完投影和视图矩阵后,进行渲染
视锥
OGRE中提供了Frustum类来模拟人眼的视觉效果,在接口上按照用户的使用习惯,方便用户转换模型坐标,而在内部实现中,通过图形学的矩阵换算,完成人体视觉和计算机视口之间的数学转换,达到一个比较好的过渡作用。视锥体类比用户在计算机中看到的图像效果图,图示大致如下:
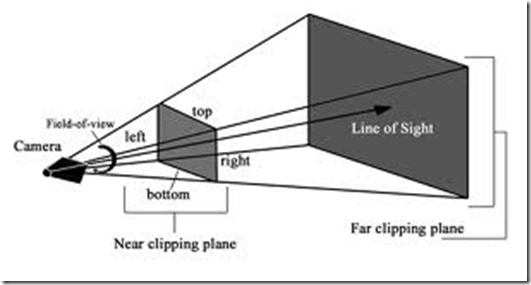
图3:Frustum类模拟
如上所示,在Frustum类中,提供的一些关键属性,而这些属性最终决定了显示的物体的位置,角度以及裁剪。类比地球,人眼则如同一颗绕地卫星,随着旋转和拉近,注视着世间万物。
Radian mFOVy;模拟人眼的角度,该角度决定了显示范围的大小,类比睁大眼睛或者眯眼看物体,
Real mFarDist; Real mNearDist;最远最近裁剪距离
根据角度,结合最远最近裁剪距离,即可获取上面的近裁剪面和远裁剪面的数据信息。
mutable Matrix4 mProjMatrix;投影矩阵,决定物体的裁剪,有最远最近裁剪面获取该矩阵数值。
投影矩阵的计算有些复杂,在OGRE中注释也只是简单的换算过程,我在初次看到时真的感叹当初实现人员的伟大(其实是OGRE的伟大和数学家在当初设计OpenGL时扎实的功底),接着就是头晕,但投影矩阵又算是相机中相对核心重要的,在这里也简单说明一下推导过程(网上很多,我本人也是阅读网络资源学习的)
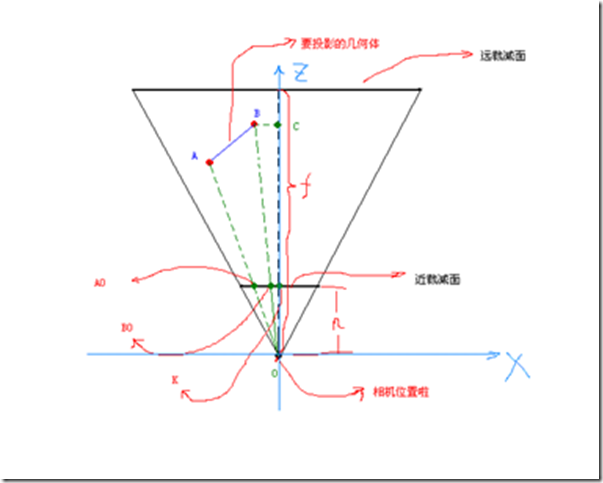
图4:投影推到
这个坐标系是DX的左手坐标系,Y向上,X向右,Z向内,几何坐标已经经过了相机坐标系的变换,相机位置为(0,0,0),假设远裁减面距离为f,近裁减面距离为n,近裁减面左边为l,右边为r,上为t,下为b。要投影的2个顶点A和B坐标分别为A(Xa,Ya,Za),B (Xb,Yb,Zb),现在我们要求他们的投影点坐标A0和B0,这里我以B点为例子,讲解投影最简单的几何知识。
首先我们来计算B0点的X坐标,(虚线都是辅助线),我们看三角形B C O和三角形B0 K O,利用初中几何知识可得他们是相似的,由相似三角形定理可知,B0 K = B C * ( n / C O );而B C等于Xb, C O等于Zb;所以Xb0 = Xb * n / Zb; 同理Yb0 = Yb * n / Zb;我们知道DX把3D坐标映射到了一个X(-1,1) Y(-1,1) Z(0,1)的一个立方体内。那现在我们就需要对投影后的坐标进行一维映射了,(其实投影就是映射,数学形式为函数,将一个值域一一映射到另外一个值域),现在在X轴上,我们要把l - r这个值域中的值一一映射到-1 - 1之间,what should we do?很显然我们有一个等式 ( x - l ) / ( r - l ) = ( x0 - ( -1) ) / ( 1 - ( -1 )); x是l - r之间的一个值,x0是-1 - 1之间的一个值,我们得到 x0 = (2x - ( r + l )) / ( r - l );这里的x换成Xb0得:x0 = (2n * Xb) / (Zb*( r - l )) - ( r + l )/( r - l );同理:y0 = (2n * Yb) / (Zb*( t - b )) - ( t + b )/( t - b ); Zb映射最简单,将n - f之间的值映射到0 - 1之间, z0 = Zb / ( f - n ) - n / ( f- n );现在我们把这些四则运算用矩阵形式来表示:
[x, y, z, 1] * [ 2n/(r-l) , 0 , 0 , 0 ]
[ 0, , 2n/(t-b) , 0 , 0 ]
[ -(r+l)/(r-l), -(t+b)/(t-b), z/(f-n) , 1 ]
[ 0, , 0 , -z*n/(f-n), 0 ]
得到的结构应该是[x0, y0, z0, w]->[x0/w, y0/w, z0/w, 1]
但为了3D引擎后期光栅化时方便的对中间象素的Z值进行线性插值,最好直接保存顶点的1/Z值,然后将1/Z嵌位到0~1之间。
[x, y, z, 1] * [ 2n/(r-l) , 0 , 0 , 0 ]
[ 0, , 2n/(t-b) , 0 , 0 ]
[ -(r+l)/(r-l), -(t+b)/(t-b), 0 , 1 ]
[ 0, , 0 , 1 , 0 ] //直接保存1/Z
将1/Z嵌位到0~1之间(线形映射) z0 = (1/Bz - 1/n)/(1/f - 1/n); [1/n->0, 1/f->1]
转换先形式使矩阵理解更加明了:z0 = f/(f-n) - f*n/((f-n)*z)
[x, y, z, 1] * [ 2n/(r-l) , 0 , 0 , 0 ]
[ 0, , 2n/(t-b) , 0 , 0 ]
[ -(r+l)/(r-l), -(t+b)/(t-b), f/(f-n) , 1 ]
[ 0, , 0 , -f*n/(f-n) , 0 ]
备注:斜体部分取自网上资料:[3D基础]投影矩阵的推导(1)
mutable Matrix4 mViewMatrix;视图矩阵,将模型和视图矩阵合为一个,负责模型显示的距离和角度。
视图矩阵相对简单一些,但也是最常用的,一般投影矩阵只要人眼的角度,最大最远距离不变,矩阵都不会变化,而视图矩阵则变化的比较平凡,角度的变化,视角的拉近拉远,人物的走动,都需要触发视图矩阵的变更,进而引起渲染的变化。
视图矩阵的推到则相对常见和简单,如果学过图形学算法,二维和三维在这方面是一样的,无怪乎平移和旋转两个矩阵,在相机中,个人感觉没有用到矩阵缩放的地方(如果三维有鹰眼的话,或许会用到,不过目前的主要应用中没有)。视图矩阵计算的数学基础不在此多说了,相信任何一本图形学教程都会有,平移和旋转的矩阵公式和推导过程。
如上,OGRE Frustum类的核心属性基本保证了相机功能在OpenGL中的简单运行。而提供的接口,则可以方便用户和上层界面来进行调用和实现自己的调度策略,OGRE尽可能在底层处理完繁杂的数学运算,给上层提供一个相对简介的接口。
另外还存在世界矩阵,这个在OGRE中并没用使用,行列式均为1,其实这个只是定义清晰一些,实际中可以和视图矩阵整合一起,OGRE本身内部也是二合一的实现思路。这个还没深入了解。
相机使用
有了视锥体类,只能获取一个角度下静态的渲染效果,而三维时一个动态,实时刷新的过程,因此,在Frustum基础上,OGRE提供了Camera类,正式推出相机的概念。
相机的作用相对简单,也比较容易理解,就是能够将Frustum的静态矩阵实时化更新,并且能够响应上层的交互操作,在OGRE中,Root中保存相机列表,实现在不同相机下对同一个场景的显示效果,物体是不变的,而相机的矩阵各不相同,达到横看成岭侧成峰的效果。
Camera类不多说了,在交互式操作中,通常鼠标和aswd键会引起移动和距离的拉伸,导致视图矩阵距离的变化,鼠标的移动则引起视图矩阵角度的变化,Camera类开发了move和rotate函数来进行视图矩阵的调整,获取最新的视图矩阵。
而在GLRenderSystem提供了set*Matrix接口,获取相机的矩阵参数值,调用OpenGL提供的矩阵接口,完成渲染,完成整个相机的转换流程(图2)
相机扩展
Camera类只是一个简单的核心相机类,用户可以根据自己的业务需要扩展各种CameraEx类来满足自己的需要,比如以地球为视图对象的相机类,则以假想地球为规则球体,地球半径来考虑最大最小裁剪距离,则很容易在Camera之上扩展出一个世界相机来,相似的道理,我们可以实现满足各种不同的扩展相机,上至星空,下至海底。
另外还要提一个缺点,OGRE在渲染时为单线程,虽然看似简单,但是其过分以过程为驱动的方式显得过于混乱,复杂不清晰,这本身并不是相机的问题,个人认为在渲染这块即使为单线程,也应该在渲染过程中以对象为基础进行架构的整理,更让代码清晰易懂,相机矩阵的设置也会清晰很多,当然,可能是我考虑不够,在实践中会暴漏其他问题吧,比如这样一个一个对象的设置反而影响效率等。