朴素贝叶斯——文本分类

朴素贝叶斯是基于贝叶斯定理于独立分布假设的分类算法

优点：在数据较少的情况下仍然有效，可以处理多分类问题。
缺点：对入输入数据的准备方式较为敏感。
使用数据类型：标称型数据。

标称型数据和数值型数据的区别：

标称型：标称型目标变量的结果只在有限目标集中取值，如真与假(标称型目标变量主要用于分类)一般在有限的数据中取，而且只存在‘是’和‘否’两种不同的结果（一般用于分类）
数值型：数值型目标变量则可以从无限的数值集合中取值，如0.100，42.001等 (数值型目标变量主要用于回归分析)

使用下面数据解释贝叶斯

头发	声音	性别
长	粗	男
短	粗	男
短	粗	男
长	细	女
短	细	女
短	粗	女
长	粗	女
长	粗	女

我们得到下面的概率分布：

性别	头发长	声音粗
男	1/3	1
女	3/5	3/5

假设头发和声音都是相互独立

男生头发长声音粗的概率=3/8*1/3*1=1/8 
女生头发长声音粗的概率=5/8*3/5*3/5=9/40 
因为1/8<9/40所以如果一个人，头发长，声音粗，那么这个人更可能是女生，于是出现这些特征就是女生。其他特征依次类推

条件概率：

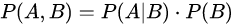
贝叶斯公式：

 由条件概率可得：

 因此得到贝叶斯的常规形式：

全概率和贝叶斯公式结合：

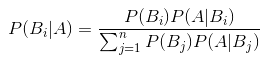
公式中，事件Bi的概率为P(Bi)，事件Bi已发生条件下事件A的概率为P(A│Bi)，事件A发生条件下事件Bi的概率为P(Bi│A)

判断头发长的人性别： 

P(男|头发长)=P(头发长|男)*P(男)/P(头发长) 
P(女|头发长)=P(头发长|女)*P(女)/P(头发长) 

判断头发长、声音粗的人性别： 

P(男|头发长声音粗)=P(头发长|男)P(声音粗|男)*P(男)/P(头发长声音粗) 
P(女|头发长声音粗)=P(头发长|女)P(声音粗|女)*P(女)/P(头发长声音粗) 

可以看到，比较最后比较概率，只用比较分子即可。也就是前面计算头发长声音粗的人是男生女生的概率

# -*- coding: utf-8 -*-
"""
Created on Mon May 18 17:53:32 2020

@author: Admin
"""


from numpy import *
import re
import random

def loadDataSet(): #创建样例数据
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  #1代表脏话
    return postingList, classVec

def createVocabList(dataSet):  #创建词库 这里就是直接把所有词去重后，当作词库
    vocabSet = set([])
    for document in dataSet:
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

#得到一个和词库长度一样的向量，该词在词库里存在，则该词在词库中的位置将被赋值1，否则0
def setOfWords2Vec(vocabList, inputSet):  #文本词向量。词库中每个词当作一个特征，文本中就该词，该词特征就是1，没有就是0
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1  #首先找到该词在词库中的位置索引，然后赋值为1 
        else:
            print("the word: %s is not in my Vocabulary!" % word)
    return returnVec


def trainNB0(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)   #上面得到的词向量中共有多少行
    numWords = len(trainMatrix[0])  #第一行有多少个元素
    pAbusive = sum(trainCategory) / float(numTrainDocs)  #label的值相加（等于3）,除以向量中共有多少行(6)
    p0Num = ones(numWords) #防止某个类别计算出的概率为0，导致最后相乘都为0，所以初始词都赋值1，分母赋值为2.
    p1Num = ones(numWords)
    p0Denom = 2
    p1Denom = 2
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    p1Vect = log(p1Num / p1Denom)  #这里使用了Log函数，方便计算，因为最后是比较大小，所有对结果没有影响。
    p0Vect = log(p0Num / p0Denom)
    return p0Vect, p1Vect, pAbusive

def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1): #比较概率大小进行判断，
    p1 = sum(vec2Classify*p1Vec)+log(pClass1)
    p0 = sum(vec2Classify*p0Vec)+log(1-pClass1)
    if p1>p0:
        return 1
    else:
        return 0

def testingNB():
    listOPosts,listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)
    trainMat=[]
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
    testEntry = ['love', 'my', 'dalmation'] # 测试数据
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
    testEntry = ['stupid', 'garbage'] # 测试数据
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))

if __name__=='__main__':
    testingNB()

问题：如果是晴天，这个人就能出去玩。这个说法是不是正确的？

P(是|晴朗)=P(晴朗|是)×P(是)/P(晴朗)

在这里，P(晴朗|是)= 3/9 = 0.33，P(晴朗)= 5/14 = 0.36，P(是)= 9/14 = 0.64

现在，P(是|晴朗)=0.33×0.64/0.36=0.60，具有较高的概率。