目录
特征选择
特征选择是从数据集的诸多特征里面选择和目标变量相关的特征,去掉那些不相关的特征。
特征选择分为两个问题:一个是子集搜索问题,另外一个是子集评价问题。比如将前向搜索和信息熵评价这两种策略进行结合就是决策树算法,事实上决策树算法可以进行特征选择。sklearn当中的“树形”算法的feature_importances_就是特征重要性的体现。
常用的特征选择分为三类:过滤式(filter),包裹式(wrapper)和嵌入式(embedding)
过滤式: 先进行特征选择,然后进行后续的训练,特征选择和后续的训练过程没有关系。
包裹式: 将机器学习的性能当做子集评价标准。
嵌入式: 将特征选择和机器学习融为一体,两者在同一个优化过程当中完成。和包裹式学习不同的是,包裹式中的子集选择和机器训练过程还是有区分的,而嵌入式将这两个过程融为一个过程。
sklearn当中的特征选择
1:移除方差较低的特征 VarianceThreshold方法
移除方差比较低的特征,使用方差作为特征选择的一个标准,是因为观察到这么一个事实,方差较低的样本差异不大,对我们的目标变量贡献比较低,所以我们移除方差比较低的样本。
举个例子,假如特征是boolean类型,那么它是伯努利随机变量,它的方差为D(X)=p(1−p)D(X)=p(1−p)。 假如我们想要移除特征当中有超过80%要么是0要么是1的样本,那么我们把方差的阈值定义为 0.8*(1-0.8)=0.16
方差=∑(x-x均值)/len(x) ,也就是 (x-x.mean()).sum()/len(x)
from sklearn.feature_selection import VarianceThreshold X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]] #样本为: ''' 0 0 1 0 1 0 1 0 0 0 1 1 0 1 0 0 1 1 ''' clf = VarianceThreshold(threshold=(0.8 * (1-0.8))) print(clf.fit_transform(X)) #fit_transform之后得到我们剔除后的数据
输出结果:
[[0 1] [1 0] [0 0] [1 1] [1 0] [1 1]]
使用variances_ 属性可以获得各个特征的方差:
print(clf.variances_) # [0.13888889 0.22222222 0.25 ]
注意:这里的VarianceThreshold和我们传统意义上面的anova(analysis of variance)没有关系。这里的VarianceThreshold方法不依赖于类的取值,只和特征本身的方差有关,所以可以用在无监督学习当中。而单因素的anova的传统应用是观察一组因素是否对我们的试验指标有显著的影响。下面的f_classif则是利用anova的原理。
2:单变量特征选择
利用统计学当中的方差假设检验的知识来对模型的特征进行选择,我在特征相似性度量中介绍了一下这些方法。
其中SelectKBest是用来选择k个最高分数的特征,SelectPercentile是选择百分比个分数最高的特征
from sklearn.datasets import load_iris from sklearn.feature_selection import SelectKBest from sklearn.feature_selection import chi2 iris = load_iris() X, y = iris.data, iris.target print(X.shape) #(150, 4) X_new = SelectKBest(chi2, k=2).fit_transform(X, y) print(X_new.shape) #(150, 2)
上面选用的是χ2测试,https://www.cnblogs.com/jiaxin359/p/8952850.html
其它的还有:对于回归问题:f_regression, mutual_info_regression 。对于分类问题有: chi2, f_classif, mutual_info_classif。
事实上在统计学当中使用的测试的结果,比如 chi2 值,还有F值等都可以转化为p值。所以SelectKBest有两种方法可以查看特征的状况,一个是scores_属性,另外一个是pvalues_属性。
k_best = SelectKBest(chi2, k=2).fit(X, y) print(k_best.scores_) #[ 10.81782088 3.59449902 116.16984746 67.24482759] print(k_best.pvalues_) #[4.47651499e-03 1.65754167e-01 5.94344354e-26 2.50017968e-15]
3: 回归特征消除
Recursive feature elimination(RFE) 是使用回归的方法,在一个模型里面不断的减少不重要的特征,最后达到我们要的特征。下面是RFE中的参数:
estimator:输入需要的模型。
n_features_to_select:需要选择的特征,默认选择半数。
step:如果大于等于1,那么每次迭代的时候去除step个,如果是0到1之间的小数,代表每次迭代去除的百分比。
下面是在手写数字识别数据集当中进行像素选择的例子:
from sklearn.datasets import load_digits from sklearn.svm import SVC from sklearn.feature_selection import RFE #RFE import matplotlib.pyplot as plt digits = load_digits() X = digits.images.reshape((len(digits.images), -1)) y = digits.target svc = SVC(kernel='linear', C=1) rfe = RFE(svc, n_features_to_select=1, step=1) # rfe.fit(X, y) ranking = rfe.ranking_.reshape(digits.images[0].shape) plt.matshow(ranking, cmap=plt.cm.Blues) plt.colorbar() plt.title("Ranking of pixels with RFE") plt.show()
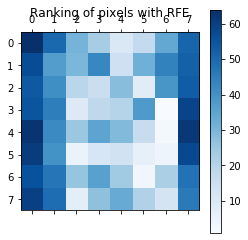
还有一个方法是RFECV,是将回归特征消除和交叉验证结合在一起了。 那么它和RFE有什么不同哪?RFE是使用模型当中的coef_或者feature_importances_这两个属性来评价特征的好坏,前者是线性模型的特征相关系数,后者是树模型的重要性。而RFECV是使用交叉验证来评估特征对模型的好坏,可以传入自己的评分函数
RFE和RFECV中重要参数
在使用RFE和RFECV的时候,有一些参数是非常重要的,参考这个博客,以selector表示我们RFE或者RFECV fit以后的模型。
selector.n_features_ :选择的特征数量
selector.support_ : 特征是否选择,返回的是n个特征的ture或者false的列表,和selector.get_support()相等
selector.ranking_ : 特征的重要排名程度
selector.grid_scores : 特征的分数
使用SelectFromModel来对特征进行选择
SelectFromModel使用了core_和feature_importances_,前者在线性模型当中使用,后者在树模型当中使用。
4:基于L1正则化的特征选择(线性模型的特征选择)。
线性模型使用L1正则化作为罚函数,在这种情况下系数当中有很多是0,这些为0的系数是不重要的系数,可以去掉,这就起到了特征选择的作用。它可以和SelectFromModel一起结合使用。
from sklearn.datasets import load_iris from sklearn.svm import LinearSVC from sklearn.feature_selection import SelectFromModel iris = load_iris() X, y = iris.data, iris.target print(X.shape) #(150, 4) lsvc = LinearSVC(C=0.01, penalty='l1', dual=False).fit(X, y) model = SelectFromModel(lsvc, prefit=True) X_new = model.transform(X) print(X_new.shape) #(150, 3)
线性模型的coef_属性,返回的是每个特征分配的权重(也就是相关系数),如果n_classes=2,那么返回的是[n_features]的大小,否则返回[n_classes,n_features]的大小。
print(lsvc.coef_) ''' [[ 0. 0.21680093 -0.28727284 0. ] [ 0. -0.09186784 0. 0. ] [-0.03499577 -0.17024796 0.13484725 0. ]] '''
5:基于树结构的特征选择:
from sklearn.datasets import load_iris from sklearn.ensemble import ExtraTreesClassifier from sklearn.feature_selection import SelectFromModel iris = load_iris() X, y = iris.data, iris.target clf = ExtraTreesClassifier() clf = clf.fit(X, y) print(clf.feature_importances_) print(X.shape) model = SelectFromModel(clf, prefit=True) X_new = model.transform(X) print(X_new.shape)
结果如下:
[0.09666543 0.06817362 0.50460169 0.33055925] (150, 4) (150, 2)
总结一下:
第一种方法和第二种方法都属于过滤式,前者利用方差信息,后者利用统计学中的单变量统计测试方法进行特征选择,特征的选择和后续的训练没有关系。 第三种方法RFE以及RFECV属于包裹式,使用递归的方法进行特征选择,使用模型的结果来进行特征评估。第四种和第五种方法分别讲了利用线性模型和树模型进行特征选择的过程,属于嵌入式。 嵌入式和包裹式的不同从上面的算法当中也可以看出来,嵌入式将模型选择和机器学习看做一个优化过程,而包裹式则是利用模型的性能当做特征的评价标准。