首先线性模型:
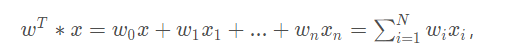
而logistic回归则通过函数L将w‘x+b对应一个隐状态p,p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数
而每一个观察到的样本(xi, yi)出现的概率是:
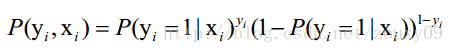
由于y的取值是(0,1),当y=1的时候,后面那一项是不是没有了,那就只剩下x属于1类的概率,当y=0的时候,第一项是不是没有了,
那就只剩下后面那个x属于0的概率(1减去x属于1的概率)。所以不管y是0还是1,上面得到的数,都是(x, y)出现的概率,所以:
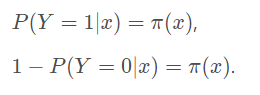
又因为,p =L(w‘x+b),即是logistic之后,而逻辑函数(即是sigmoid函数)又等于:
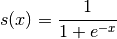
所以:(其实这里已经推导出来的逻辑回归表达式)

后面的是损失函数了
整合为似然函数为:

对数似然函数为(log减就是除):前面少了log,最后面少了大括号]
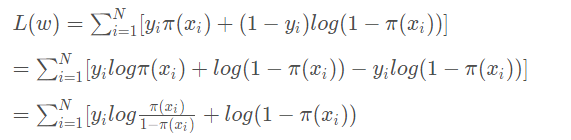
令:
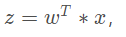
得到:
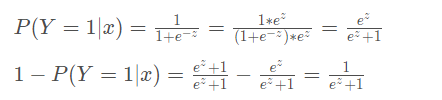
而又有:
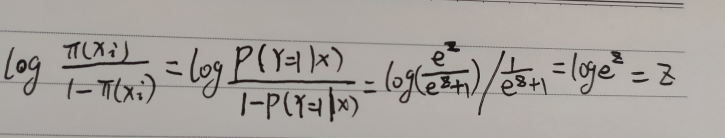
代入对数似然函数 (L(w)少了log()) :
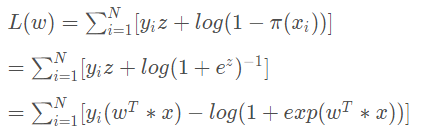
也可以这样表达:
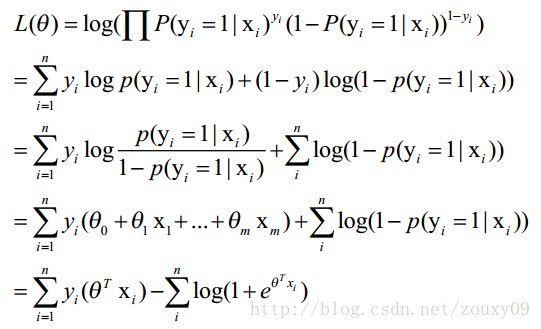
这时候为求最大值,对L(θ)对θ求导,得到:
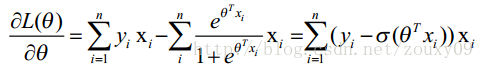
求导太复杂了,就不求导了
逻辑回归的最终模型为:
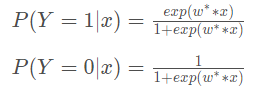
转换一下:
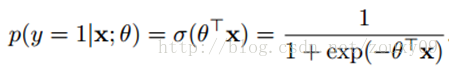
============================================================
这步我主要看求导部分,也就是求参数的最小值
