前言
为了对比不同策略的效果,如新策略点击率的提升是否显著,常需要进行A/B测试。但测试是有成本的,样本量小时不能判断出差异是否是由抽样误差引起,样本量太大时如果效果不好则会造成难以挽回的损失。如何科学地选择样本量呢?需要了解A/B测试的统计学原理
一、 A/B测试的统计学原理
(一)大数定律和中心极限定理
A/B 测试样本量的选取基于大数定律和中心极限定理。通俗地讲:
1. 大数定律:当试验条件不变时,随机试验重复多次以后,随机事件的频率近似等于随机事件的概率。
2. 中心极限定理:对独立同分布且有相同期望和方差的n个随机变量,当样本量很大时,随机变量
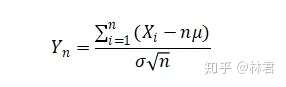
近似服从标准正态分布N(0,1)。
根据大数定律和中心极限定理,当样本量较大(大于30)时,可以通过Z检验(也称U检验,是为了检验在零假设情况下测试数据能否可以接近正态分布的一种统计测试)来检验测试组和对照组两个样本均值差异的显著性。

注:样本量小于30时,可进行t检验。
(二)假设检验
在进行假设检验时,我们有两个假设:原假设H0(两个样本没有显著性差异)和备择假设H1(两个样本有显著性差异)。相应地,我们可能会犯两类错误:
第I类错误:H0为真,H1为假时,拒绝H0,犯第I类错误(即错误地拒绝H0)的概率记为alpha。
第II类错误:H0为假,H1为真时,接受H0,犯第II类错误(即错误地接受H0)的概率记为beta。
1. 犯第I类错误的概率alpha与置信水平1-alpha
通常,将犯第I类错误的概览alpha(0.05)称为显著性,把没有1-alpha(0.95)称为置信水平,即有1-alpha的概率正确接受了H0。
一般,alpha取值为0.05或更小的数值,即容忍犯第I类错误的概率最大为alpha。
2. 犯第II类错误的概率beta与统计功效power=1-beta
通常,将犯第II类错误的概率称为beta;将1-beta称为统计功效,即正确拒绝H0的概率。
一般,beta取10%~20%,则统计功效的取值为80%~90%。

犯第一类错误的概览alpha与犯第二类错误的概览beta之间的关系如下图:

3. 统计显著性p-value
当p-value<alpha时,即原假设成立的概率小于预设的显著性水平,可拒绝原假设。p-value只说明两个样本有没有显著性差异,并不说明差异的大小。
根据统计学原理计算样本量,需要根据显著性水平查正态分布表,工作中用到的比较少,这里省略。
工作中可用python中的已有的包和函数计算。
二、样本量计算的python实现
Python统计包statsmodels.stats.power中,有一个NormalIndPower工具,可以用其中的solve_power函数实现。
Solve_power函数中的参数如下:
(1)参数effect_size : 两个样本均值之差/ 标准差 (原来样本值*(1-原来样本值))的开方
(2)nobs1:样本1的样本量,样本2的样本量=样本1的样本量*ratio
(3)alpha:显著性水平,一般取0.05
(4)power:统计功效,一般去0.8
(5)ratio: 样本2的样本量/样本1的样本量,一般取1
(6)alternative:字符串str类型,默认为‘two-sided’,也可以为单边检验:’larger’ 或’small’
例:目前的点击率CTR是0.3,我们要想提升10%,将点击率提升到0.33,测试组和对照组的样本量相同。
计算如下:
from statsmodels.stats.power import NormalIndPower import math effect_size = 0.03/math.sqrt(0.3*(1-0.3)) ztest = NormalIndPower() num = ztest.solve_power( effect_size = effect_size, nobs1 = None, alpha = 0.05, power= 0.8, ratio=1, alternative = 'two-sided') print (num)
3662.8015711721328
注意,得到的值是总的样本数量,每组还得除以组数;检测效果变化值越小,需要的样本量越大;检测效果变化值越大,需要的样本量越小。因为,变化效果越小,越有可能是抽样误差引起的;为了避免抽样误差的影响,需要增大样本量。
https://abtestguide.com/abtestsize/
使用Z检验需要知道方差,但是我们一般都是不知道方差的,因此下面还可以只用卡方检验
三、卡方检验
- Z检验,即检验实验组与对照组服从分布的均值是否相等
- 卡方检验,即检验实验组是否服从理论分布(将对照组看成理论分布)
求解过程python
from statsmodels.stats.power import GofChisquarePower GofChisquarePower().solve_power( effect_size=None, nobs=None, alpha=None, power=None, n_bins=2, )