Box-Cox转换

1.适用变量

连续的变量不满足正态分布的情况，一般是对因变量y进行转换，但是其实连续的自变量也是可以转换的

 

2.如何判断变量是否满足正态分布

#使用ks检验：
#导入scipy模块
from scipy import stats

"""
kstest方法：KS检验，参数分别是：待检验的数据，检验方法（这里设置成norm正态分布），均值与标准差
结果返回两个值：statistic → D值，pvalue → P值
p值大于0.05，为正态分布
H0:样本符合  
H1:样本不符合 
如何p>0.05接受H0 ,反之 
"""
u = s['value'].mean()  # 计算均值
std = s['value'].std()  # 计算标准差
stats.kstest(s['value'], 'norm', (u, std))

 

3.Box-Cox转换的优势

Box-Cox变换的目的是为了让数据满足线性模型的基本假定，即线性、正态性及方差齐性

 

4.什么时候用Box-Cox

对于非正太数据的转换方法有：

在一些情况下（P值<0.003）上述方法很难实现正态化处理，所以优先使用Box-Cox转换，但是当P值>0.003时两种方法均可，优先考虑普通的平方变换。

至于为什么是0.003？？

 5.知道什么时候使用了，但是参数值怎么选择

y_boxcox = special.boxcox1p(y, lam_best) 利用llf获得优化后的lambda或boxcox_normmax(x) 得到优化后的lambda

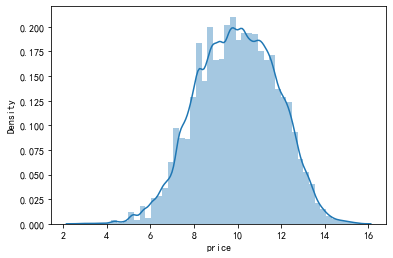
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 13 09:55:46 2021

@author: Administrator
"""

#导入需要的模块

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import pycard as pc

train_data =pd.read_csv('D:/迅雷下载/used_car_train_20200313.csv',sep=' ')

#%%计算p值
#使用ks检验：
#导入scipy模块
from scipy import stats

"""
kstest方法：KS检验，参数分别是：待检验的数据，检验方法（这里设置成norm正态分布），均值与标准差
结果返回两个值：statistic → D值，pvalue → P值
p值大于0.05，为正态分布
H0:样本符合  
H1:样本不符合 
如何p>0.05接受H0 ,反之 
"""
u = train_data['price'].mean()  # 计算均值
std =train_data['price'].std()  # 计算标准差
s,p = stats.kstest(train_data['price'], 'norm', (u, std))  #(0.21608994799012532, 0.0)


#%%计算最佳的lambda

from scipy import stats,special

 
lam_range = np.linspace(-2,5,100)  # default nums=50
llf = np.zeros(lam_range.shape, dtype=float)

y = train_data['price']
 
# lambda estimate:
for i,lam in enumerate(lam_range):
    llf[i] = stats.boxcox_llf(lam, y)        # y 必须>0
 
# find the max lgo-likelihood(llf) index and decide the lambda
lam_best = lam_range[llf.argmax()]
print('Suitable lam is: ',round(lam_best,2))
print('Max llf is: ', round(llf.max(),2))
 

y_boxcox = special.boxcox1p(y, lam_best)

# 逆转换:
y_invboxcox = special.inv_boxcox1p(y_boxcox, lam_best)

#%%画图
plt.figure(1)
sns.distplot(train_data['price'])
plt.figure(2)
sns.distplot(y_boxcox)

#%%计算转换之后的p值
u = y_boxcox.mean()  # 计算均值
std =y_boxcox.std()  # 计算标准差
s,p = stats.kstest(y_boxcox, 'norm', (u, std))  #(0.02719269319870718, 8.643971208421137e-97)

然而经Box-Cox变换后数据是否同时满足了以上假定，仍需要考察验证，虽然图片看着比之前好很多，但是仍然不能不满足正态分布