sympy库的使用（一）定义和表达式简化等等

下一个学习对象

网址：https://docs.sympy.org/latest/tutorial/intro.html#what-is-symbolic-computation

 

1.导入sympy

from sympy import *

我大致看了下，这个属性、类、方法太多了，就不一一铺出来了

2.使用前先定义(symbols)

由于我们是应用，因此不纠结具体的细节

x = symbols('x')
x+1  #x + 1

#多变量时，记得使用空格隔开
x,y,z = symbols('x y z')

 默认是变量，但是其实我们也可以定义函数

f, g = symbols('f g', cls=Function)
f(x)

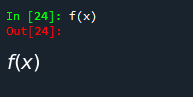
3.怎么定义表达式

f = x+1
f1 = x+y+z

就是一个等号，和我们变量赋值是一样的

当然里面的表达式你可以使用各种各样的，比如三角函数，幂函数，指数等等

 

4.替换（subs）

替换有什么作用：

1.用数值替换变量，相当于将值代入变量里面去解题，类似于当x=1,y=2之类的

2.用变量替代变量，方便我们不用重复写表达式，，比如说f=cos(x) ,f1=cos(y),直接替换可以节约时间

3.注意sympy表达式是不可变的，替换并不能改变它原值

from sympy import *
x,y,z = symbols('x y z')
expr = cos(x) + 1
expr.subs(x,y)  #输出 cos(y) + 1
expr # cos(x) + 1 说明这个替换并没有改变原值

#数值替换变量
expr.subs(x,0)  #输出是2 

#变量替换变量
expr = x**y
expr  #x**y

expr = expr.subs(y,x**y)
expr   #x**(x**y)

#可以多个变量同时进行替换
expr = x**3 + 4*x*y - z
expr.subs([(x,2),(y,4),(z,0)])  #65536

5.将字符串转换为Smpy表达式(sympify)

字符串里面使用的变量要求是定义好的，不然虽然不报错，但是使用么有定义的也没有用处

str_expr = 'x**2+3*x-1/2'
expr = sympify(str_expr)
expr #输出 x**2 + 3*x - 1/2

#试试如果变量没有定义，能否使用
str_expr = 'x**2+3*x-g'
expr = sympify(str_expr)
expr #输出 -g + x**2 + 3*x
g #NameError: name 'g' is not defined

6.将无理数转换为浮点型（求出近似值）（evalf）

作用：

1.如果表达式是数值，可将这表达式以浮点型输出，一般默认精度是15位，用户可以自己设置

2.如果表达式有变量，可以配合subs一起求值，subs以字典传入

expr = sqrt(8)
expr #输出2*sqrt(2)

expr.evalf()  #2.82842712474619

#默认使用15位精度,也可以自己设置精度参数
pi.evalf(10) #3.141592654


#对于非数值表达式，可以配合和subs使用,但是subs要以字典传入
expr = cos(2*x)
expr.evalf(subs={x:2.4})  #0.0874989834394464

7.类似于lambda的函数lambdify

看是官网不是很清楚，但是它于lambda使用方法差不多，那就是按照这个lambda去理解

import numpy 

a = numpy.arange(10)
a #array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

expr = sin(x)
f = lambdify(x,expr,'numpy')
f(a)  
'''
array([ 0.        ,  0.84147098,  0.90929743,  0.14112001, -0.7568025 ,
       -0.95892427, -0.2794155 ,  0.6569866 ,  0.98935825,  0.41211849])
'''

#math
f = lambdify(x,expr,'math')
f(0.1)  #0.09983341664682815

#自定义的函数，使用字典形式
def mysin(x):
    return x

f = lambdify(x, expr,{'sin':mysin})
f(1)  #1

8.简化表达式simplify

通过只能方法，简化数学表达式，但是不是所有的表达式可以简化的，不能简化的输出原来的

from sympy import init_printing
init_printing(use_unicode=True)

#简化表达式
simplify(sin(x)**2+cos(x)**2)  #1
simplify((x**3 + x**2 - x - 1)/(x**2 + 2*x + 1)) #x - 1
simplify(gamma(x)/gamma(x - 2)) #(x - 2)⋅(x - 1)

#不能简化
simplify(x**2 + 2*x + 1) 

9.多项式展开expand()

说是多项式的展开，比如说(x+y)*(x+y)展开，得到 x**2+y**2+2*x*y

expand((x+1)**2)
expand((x+2)*(x-3))
expand((x + 1)*(x - 2) - (x - 1)*x)

'''
x**2 + 2*x + 1
x**2 - x - 6
-2
'''

10.factor与expand相反的效果

factor(x**3 - x**2 + x - 1)

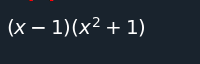
factor(x**2*z + 4*x*y*z + 4*y**2*z)

11.collect()

不知道怎么说这个，自己看效果吧

expr = x*y + x - 3 + 2*x**2 - z*x**2 + x**3
expr

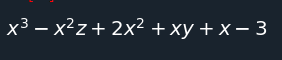
collected_expr = collect(expr, x)
collected_expr

 collect()与该.coeff() 方法结合使用时特别有用。 给出x的系数：expr.coeff(x, n)x**nexpr

也就是多少次方对于的系数

collected_expr.coeff(x, 0)  #-3
collected_expr.coeff(x, 1)  #y+1
collected_expr.coeff(x, 2)  #2-z
collected_expr.coeff(x, 3)  #1

12.cancel()弄成分数的形式

 看例子比较好理解

注意这个最后结果是不可约了，最简化的了

expr = 1/x + (3*x/2 - 2)/(x - 4)
expr

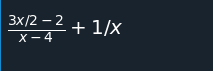
cancel(expr)

13.aqart对有理函数执行部分分数分解

还是看图吧，很多术语都忘记得差不多了

expr = (4*x**3 + 21*x**2 + 10*x + 12)/(x**4 + 5*x**3 + 5*x**2 + 4*x)
expr

apart(expr)