在介绍幂简化函数之前,需要对幂持有的恒等式进行数学讨论。
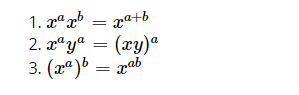
上面的表达式是否恒成立,显然后面2条是有条件的

要记住这一点很重要,因为默认情况下,如果通常不正确,SymPy将不会执行简化
但是我们有时候又需要对这些数据进行简化,那么首先得定义好定义域
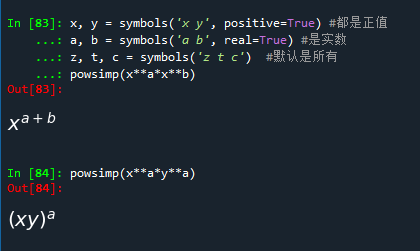
x, y = symbols('x y', positive=True) #都是正值 a, b = symbols('a b', real=True) #是实数 z, t, c = symbols('z t c') #默认是所有
感觉最重要的知识就是这三个等式以及定义域,就不再写了
1.powsimp简化
x, y = symbols('x y', positive=True) #都是正值 a, b = symbols('a b', real=True) #是实数 z, t, c = symbols('z t c') #默认是所有 powsimp(x**a*x**b) powsimp(x**a*y**a)
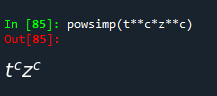
请注意,powsimp()如果无效,则拒绝进行简化。
powsimp(t**c*z**c)
非要简化,可以使用force=True标志,无论假设如何,都将迫使进行简化
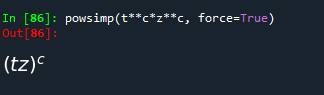
powsimp(t**c*z**c, force=True)