sympy库的使用（五）阶乘，微分，积分，极限等

https://docs.sympy.org/latest/tutorial/calculus.html

本文主要记录一些特殊的函数，比如阶乘啊，二项分布等等

首先定于变量

x, y, z = symbols('x y z')
k, m, n = symbols('k m n')

 

 一、阶乘factorial

n! = 1*2*3*...(n-1)*n

factorial(n)

 解阶乘

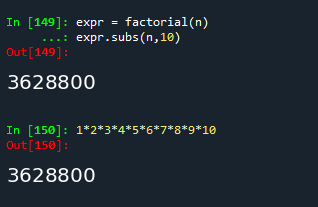
expr = factorial(n)
expr.subs(n,10)  

二、二项式binomial

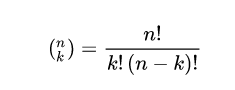
注意n>k，且都为正整数

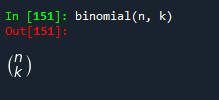
binomial(n, k)

 解二项式

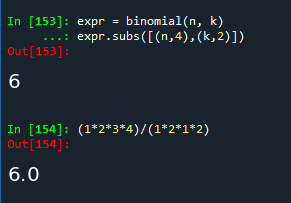
expr = binomial(n, k)
expr.subs([(n,4),(k,2)])

三、微积分

1.求导diff函数

from sympy import *
x, y, z = symbols('x y z')
init_printing(use_unicode=True)

diff(cos(x), x)
diff(exp(x**2), x)

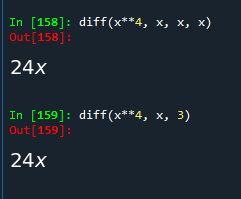
 diff求一阶导，二阶导，三阶导，有2中表达方式，一种是在后面一直写x,x,x,一种是直接在后面写对应的数字，写2就是二阶导

#方法一
diff(x**4, x, x, x)
#方法二
diff(x**4, x, 3)

 diff也可以解多元的偏导，但是要记住每次解导数的时候都是在前面一次的结果上再求导数

expr = 2*x*y**2*z**4
diff(expr, x, y,  z)
diff(expr, x, y, 2, z, 4)
diff(expr, x, y, y, z, 4)

还可以写成expr.diff()

expr.diff(x, y, y, z, 4)

2.求偏导

deriv = Derivative(expr, x, y, y, z, 4)
deriv

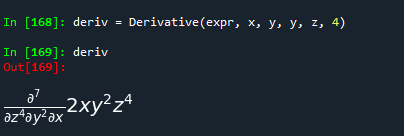
 写成偏导的形式，再求解

deriv.doit()

 diff还可以对不是表达式中的变量进行求导，比如下面的n并不是表达式中的变量，但是我们也可以对此求偏导

m, n, a, b = symbols('m n a b')
expr = (a*x + b)**m
expr
expr.diff((x, n))

四、积分

要计算积分，请使用integrate函数。有两种积分，定积分和不定积分，不定积分和定积分怎么区别？

请注意，SymPy不包含积分常数。如果需要，可以自己加一个，也可以将问题改写为微分方程并用于dsolve求解，这确实会增加常数

1.不定积分

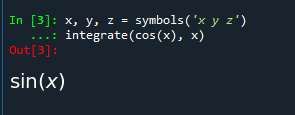
即反导数或基元，只需在表达式后传递变量

import pycard as pc
from sympy import *
import sympy
from sympy import init_printing
init_printing(use_unicode=True)

x, y, z = symbols('x y z')
integrate(cos(x), x)

 2.定积分

要计算定积分，请传递参数。例如，要计算(integration_variable, lower_limit, upper_limit)

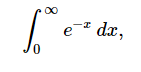
integrate(exp(-x), (x, 0, oo)) #1

可以传递多个限制元组以执行多个积分。例如，要计算

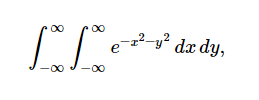
integrate(exp(-x**2 - y**2), (x, -oo, oo), (y, -oo, oo))  #π

如果integrate无法计算积分，则返回未评估的 Integral对象

integrate(x**x, x)

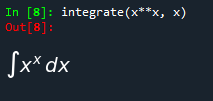
 创建未评估的积分 Integral。如果要解积分，请调用doit。

expr = Integral(log(x)**2, x)
expr

expr.doit()

 integrate使用了不断改进的强大算法来计算定积分和不定积分，包括启发式模式匹配类型算法，Risch算法的部分实现以及使用Meijer G函数的算法，该算法 可用于根据特殊函数计算积分，特别是定积分

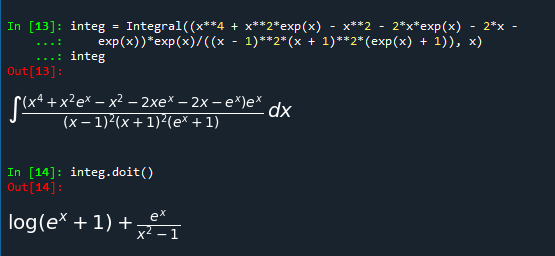
integ = Integral((x**4 + x**2*exp(x) - x**2 - 2*x*exp(x) - 2*x -
    exp(x))*exp(x)/((x - 1)**2*(x + 1)**2*(exp(x) + 1)), x)
integ
integ.doit()

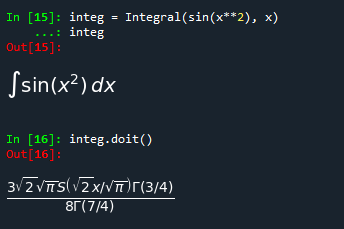
integ = Integral(sin(x**2), x)
integ

integ.doit()

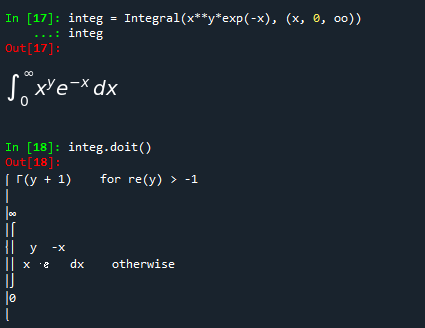
integ = Integral(x**y*exp(-x), (x, 0, oo))
integ

integ.doit()

五、极限

SymPy可以使用该limit函数计算符号极限。计算语法

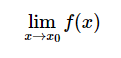
 使用limit(f(x), x, x0)

下面这个例子是x越接近0，f(x)最接近1

limit(sin(x)/x, x, 0)  #1

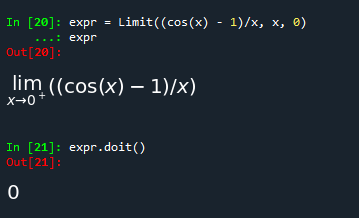
limit有一个未评估的对应物Limit。要对其进行评估，请使用doit。这句话说，可以先写出表达式，然后再计算极限

expr = Limit((cos(x) - 1)/x, x, 0)
expr

expr.doit()

 要仅在一侧评估极限，请将'+'或'-'作为第四个参数传递给limit。例如，要计算

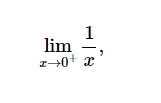
limit(1/x, x, 0, '+')  #∞
limit(1/x, x, 0, '-')  #-∞