前向计算:没啥好说的,一层一层套着算就完事了 y = f( ... f( Wlayer2T f( Wlayer1Tx ) ) )
反向求导:链式法则

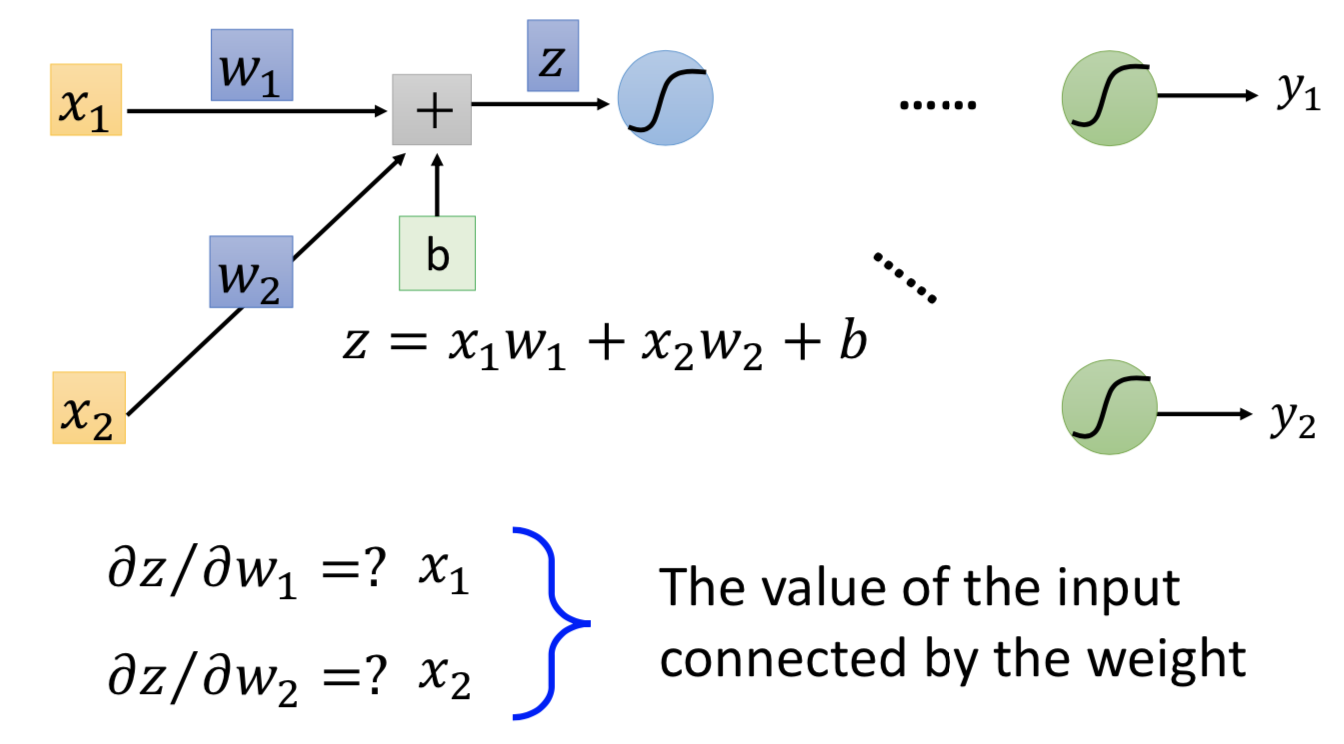
单独看一个神经元的计算,z (就是logit)对 wi 的偏微分等于 xi :
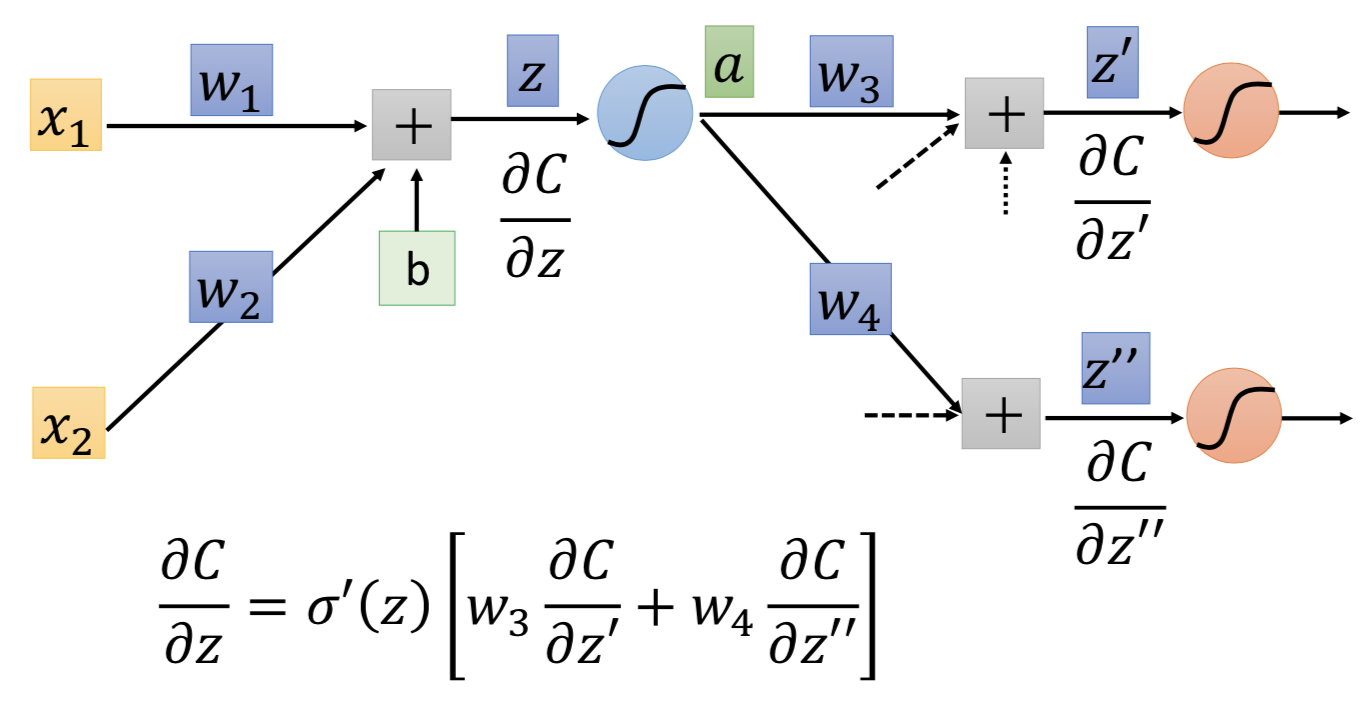
再看多层的情况,z 经过 激活函数得到 a,而 a 在下一层和 w3 、w4 都进行了计算。所以 C 对 z 求偏微分的话,根据链式法则这两条参数的路径都要去找,且 z' 对 a 的偏微分等于w3,z'' 对 a 的偏微分等于w4 :
![]()
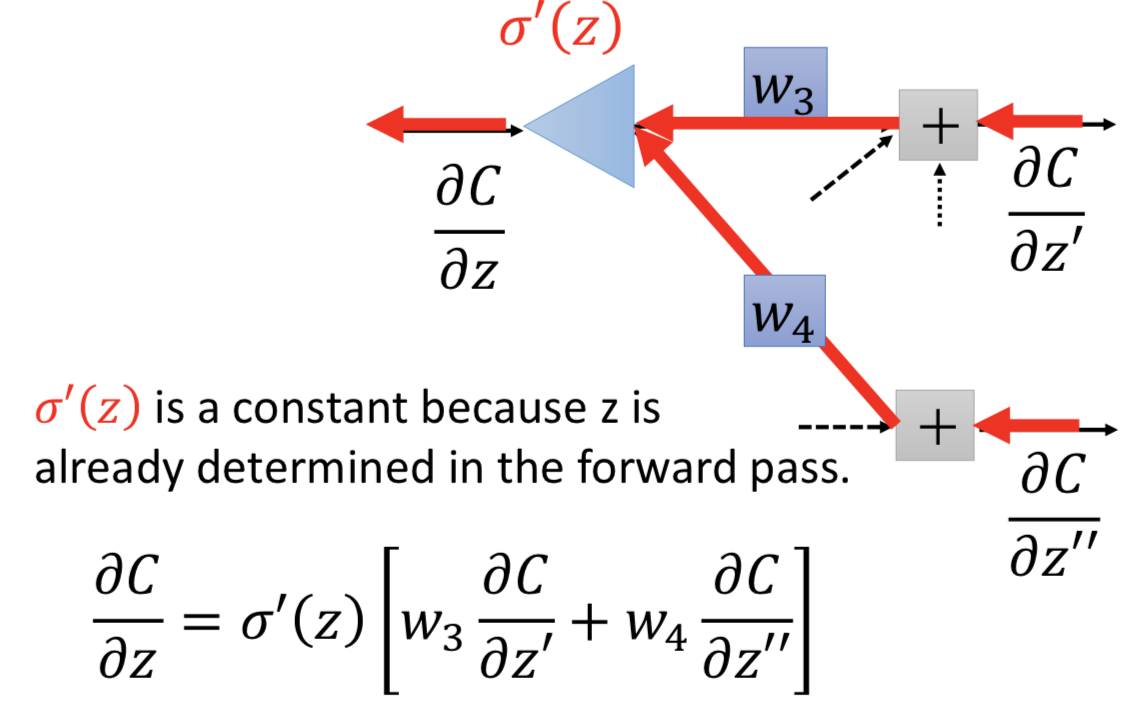
到这里重点来了,想象有一个不存在神经元,做的计算跟上面这个式子一样,那差不多就是下图这样,z 已经在之前就计算出来了
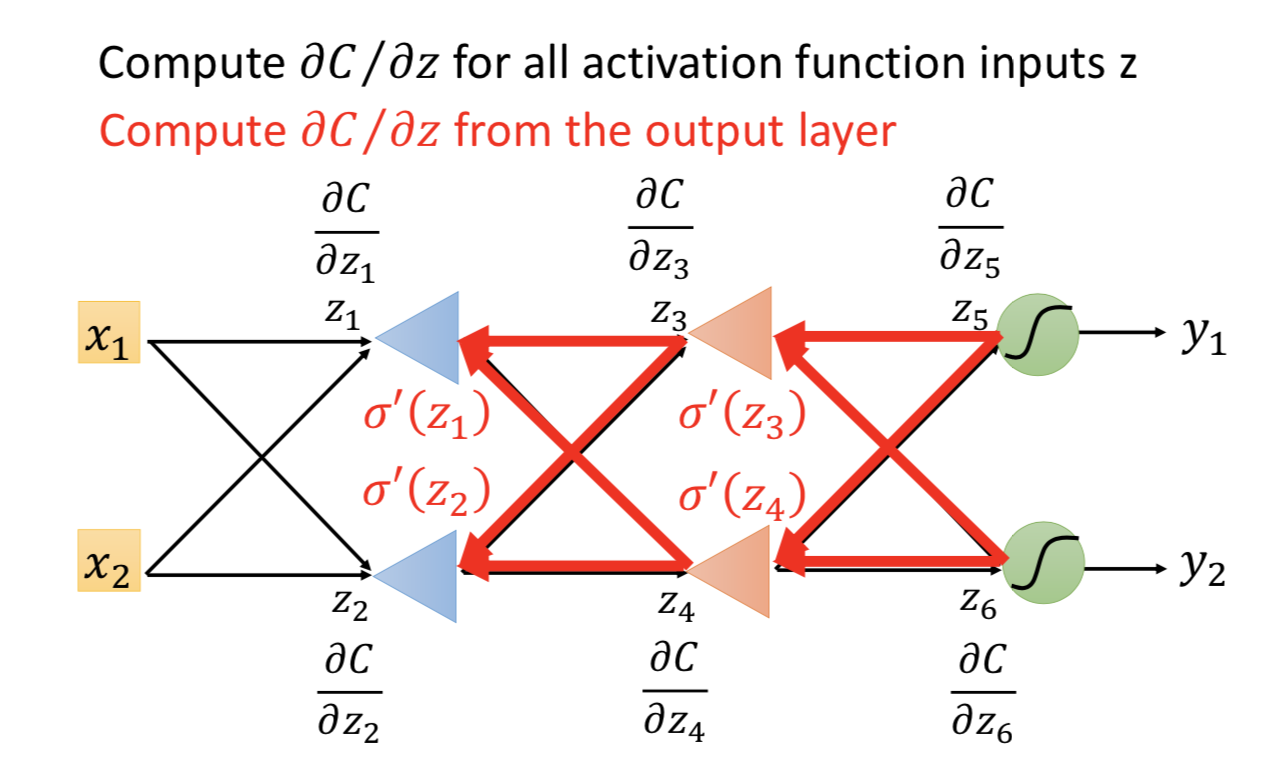
最后,就差两项偏微分没有计算出来,两种情况:
1. 当前就已经是output layer了,那就直接算
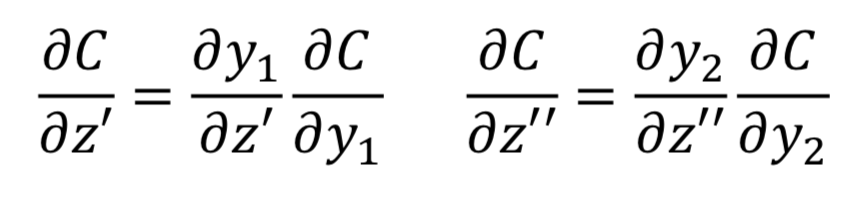
完事了
2. 还不是output layer
继续跟刚才的 backward pass 一样计算,一直找到最后
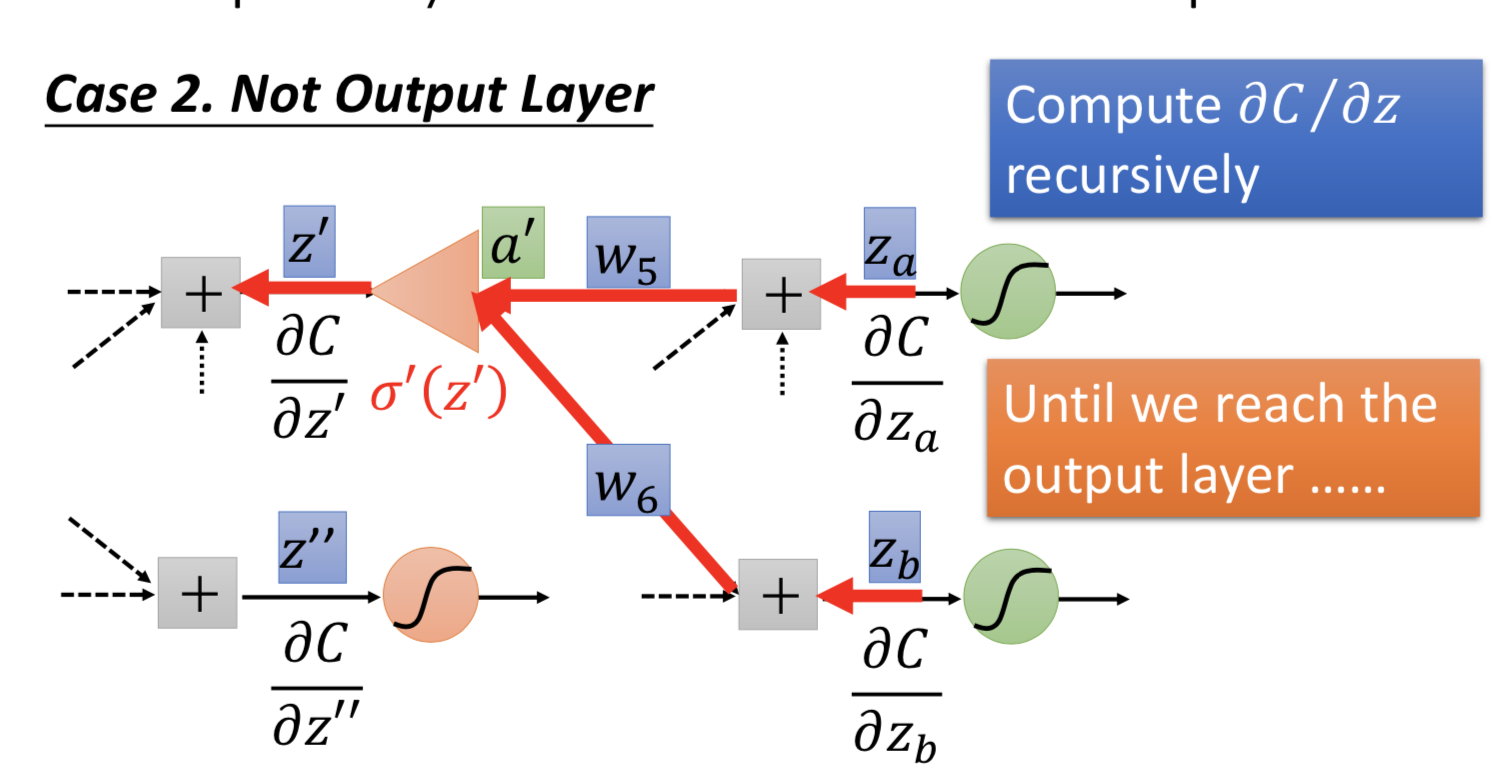
所以有没有真正理解什么是反向传播?
其实跟前向传播的计算并没有很大区别,实际上可以理解为:假设存在一个神经元是放大器的反向网络进行计算,而且weight是一样的。
先算最后一层的偏微分,再一路往前面的层推过去,由于 sigmoid 函数的求导性质,所有反向计算需要的算子都是前向计算过程中已经算过的。(所以前向计算的时候每一层的结果都找个 list 先存一下)