并查集

并查集 union & find

 

是一种树型的数据结构，用于处理一些不交集（Disjoint Sets）的合并及查询问题。一般用数组实现。

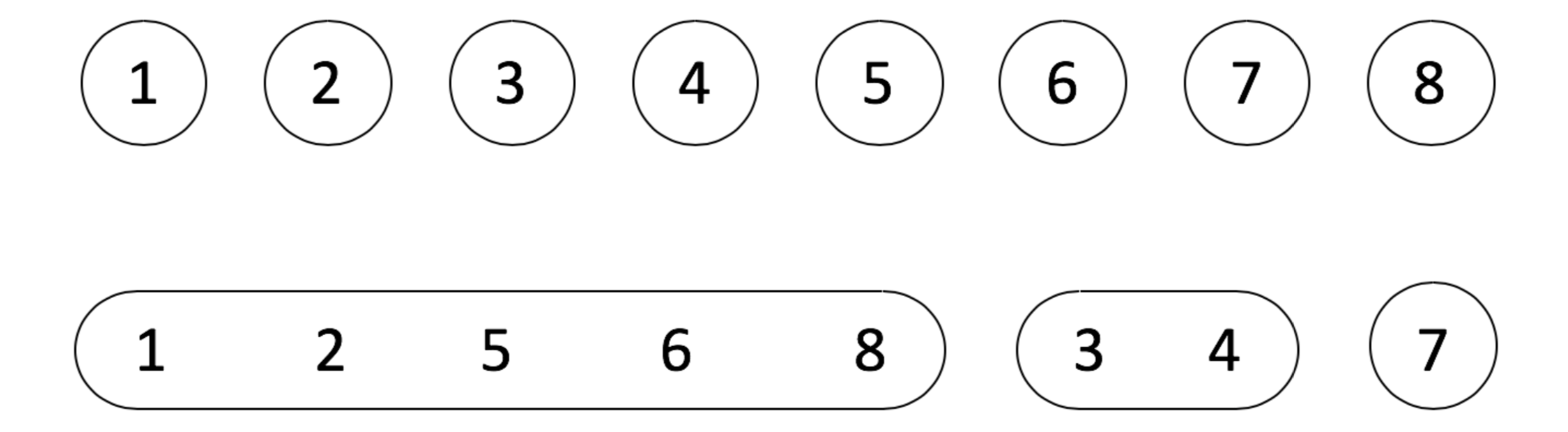
Find：确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

Union：将两个子集合并成同一个集合。

在现实生活中的例子

1. 小弟 => ⽼大

2. 帮派识别

3. 两种优化⽅方式：小组织和大组织合并时的优化、路径压缩

并查集的初始化，每个元素的root指向自己：

根据合并关系改变元素的root指向，两个集合的合并就是把一个集合的尾部的root指向另一个集合的尾部：

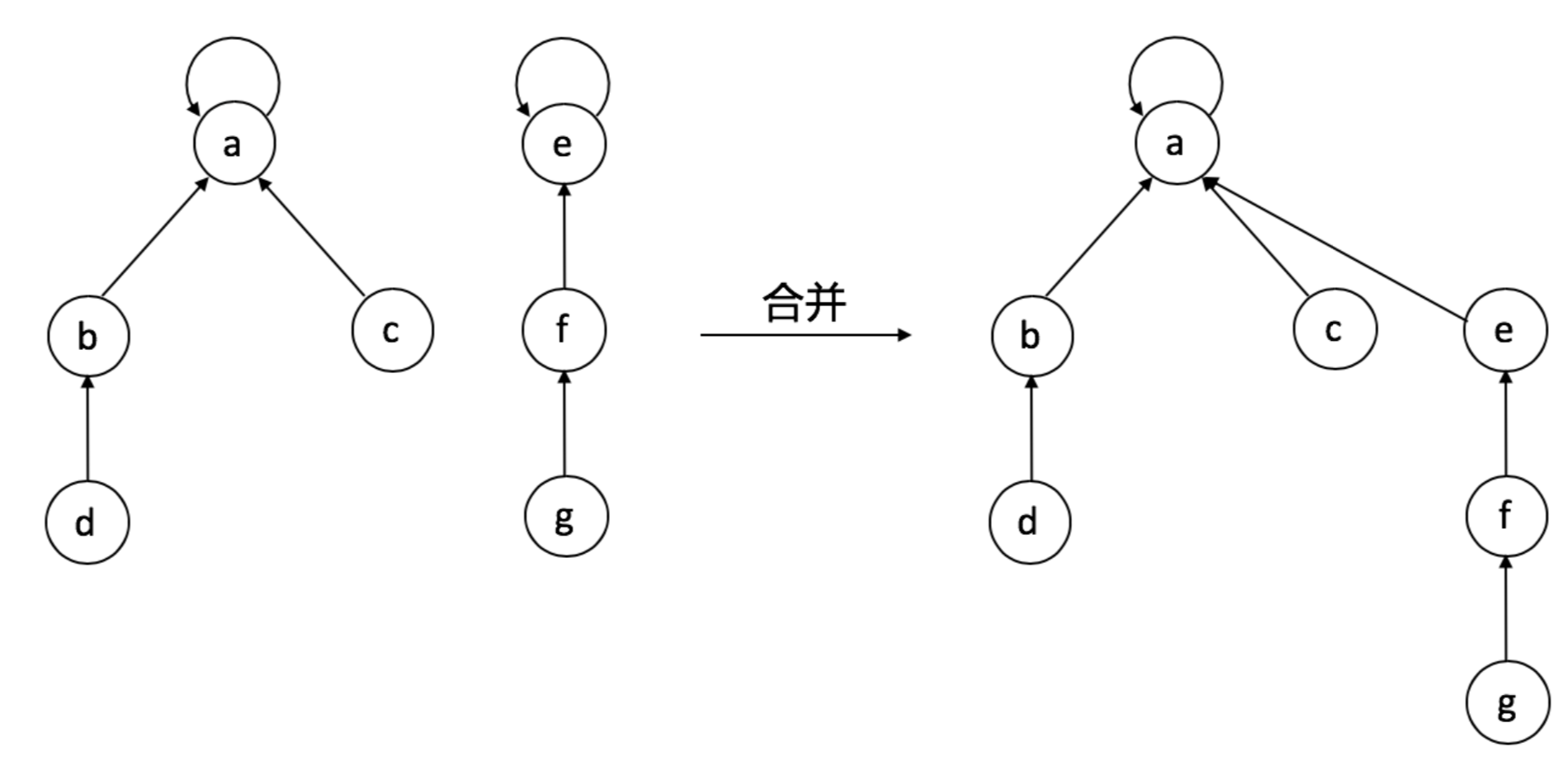
function MakeSet(x)
    x.parent := x

function Find(x)
    if x.parent == x:
        return x
    else:
        return Find(x.parent)

function Union(x, y):
    xRoot := Find(x)
    yRoot := Find(y)
    xRoot.parent := yRoot

　　

并查集优化

1. 合并子集时，显然右边并查集的深度（rank）小的情况更好，便于搜索root。把深度较低的子集 merge 到深度较高的子集中去。

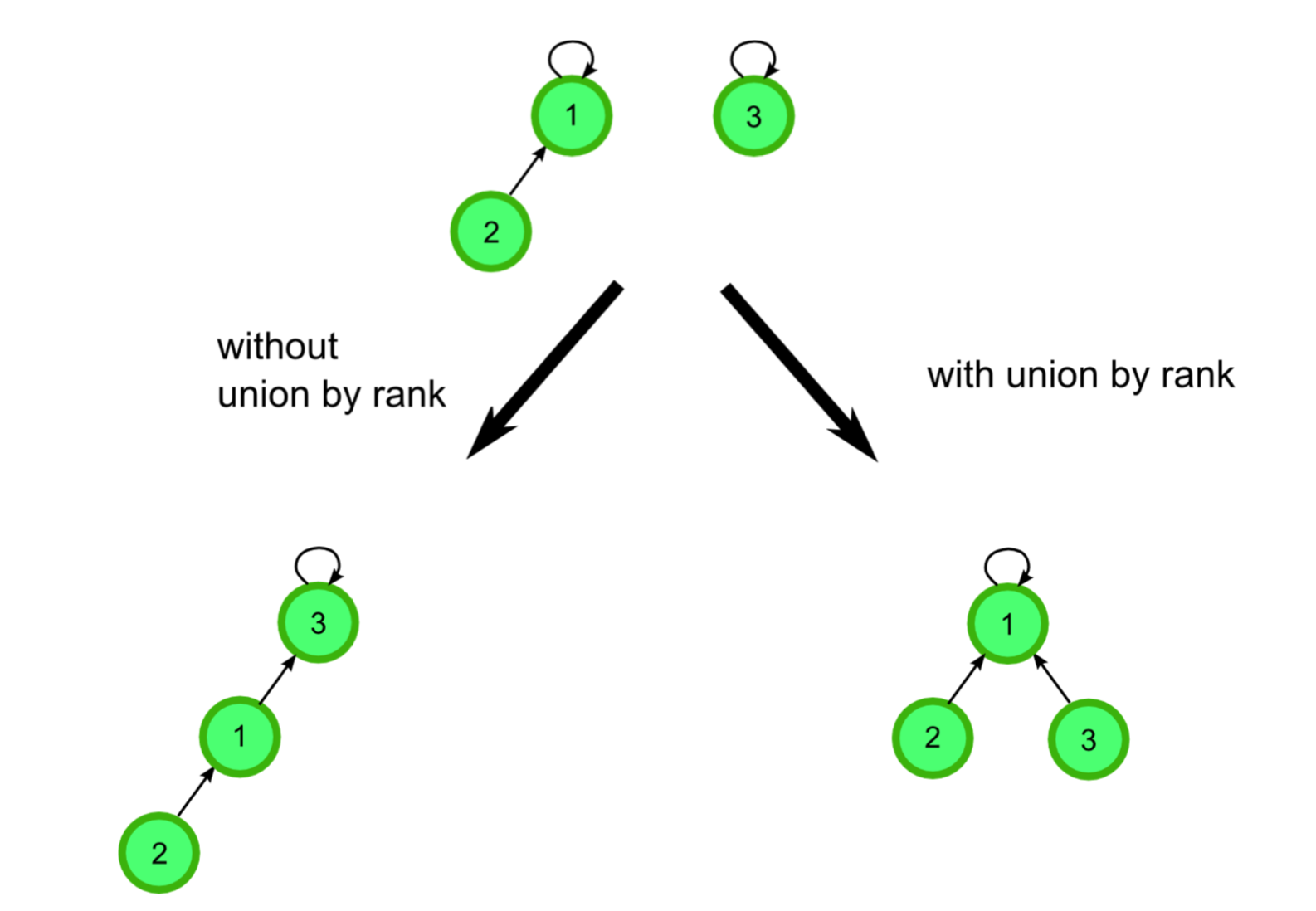
function Union(x, y):
    xRoot := Find(x)
    yRoot := Find(y)
    if xRoot == yRoot:
        return

    if xRoot.rank < yRoot.rank:
        xRoot.parent := yRoot
    
    else if xRoot.rank > yRoot.rank:
        yRoot.parent := xRoot

    else:
        yRoot.parent := xRoot
        xRoot.rank += 1

 2. 更有效，路径压缩。一般做了这个优化，优化一就可做可不做了。

class QuickUnionUF:
    roots = []
    count = 0

    def __init__(self, n):
        self.count = n
        for i in range(n):
            self.roots.append(i)
    
    def isConnected(self, p, q):
        if self.find(p) == self.find(q):
            return True
        return False
    
    def find(self, p):
        root = p
        while root != self.roots[root]:
            root = self.roots[root]
        # 路径压缩
        while p != self.roots[p]:
            tmp = self.roots[p]
            self.roots[p] = root
            p = tmp
        return root

    def union(self, p, q):
        pRoot = self.find(p)
        qRoot = self.find(q)
        self.roots[pRoot] = qRoot