其实这个题目已经有很多人写过了,数学之美里就有,最近阮一峰的博客里也写了,本文基本上遵循的就是他的思路,只是让其看起来再小白一点点。其实说白了就是用自己的话,再把同样一件事描述一下,顺便扩扩句,把其中跳跃比较大的部分再补充补充。 阮一峰的原文:http://www.ruanyifeng.com/blog/2013/03/cosine_similarity.html
当然虽然题目是比较两篇文章的相似性,但我们也不会傻到真拿两篇篇文章来说明,为了简单起见,我们从句子着手。
句子A:周杰伦是一个歌手,也是一个叉叉
句子B:周杰伦不是一个叉叉,但是是一个歌手
如何比较相似性呢 ?
第一步 分词
句子A : 周杰伦/是/一个/歌手,也/是/一个/叉叉 (注:假设分词也是个牛叉叉,可以识别叉叉这个词) 句子B: 周杰伦/不/是/一个/叉叉 ,但是/是/一个/歌手
第二步 去重复,列出识别的所有单词
周杰伦、是 、不、一个、叉叉 、歌手、但是、也
第三步 计算词频(这里表示某个词在一个句子里出现的次数)
句子A: 周杰伦1、是2 、不 0 、一个2、叉叉1、歌手1、但是0、也1 句子B: 周杰伦1、是2 、不 1 、一个2、叉叉1、歌手1、但是1、也0
第四步 构造词频向量
句子A [1 , 2 , 0 , 2 , 1 , 1 , 0 , 1] 句子B [1 , 2 , 1 , 2 , 1 , 1 , 0 , 1]
上面构造的是两个多维的向量,其中每个维度的值就是词频。
OKAY,构造出了上面的二个多维向量后,比较两句话的相似度就 变成了比较这两个向量的相似度了。任何问题只要一变成数学问题,基本上就好解决了 :) ... ...
那么如何比较两个向量的相似度呢 。先来点高中数学知识 。
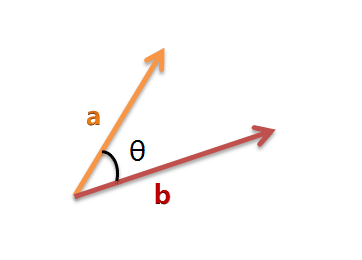
上图是一个二维向量的几何表示。其中有2个二维向量a和b 。 θ 就是这2个二维向量的夹角;如果夹角为0度,意味着方向相同、线段重合;如果夹角为90度,意味着形成直角,方向完全不相似;如果夹角为180度,意味着方向正好相反。因此,我们可以通过夹角的大小,来判断向量的相似程度。夹角越小,就代表越相似。
再复习一个初中的知识:余弦定理 (应该是初中吧)
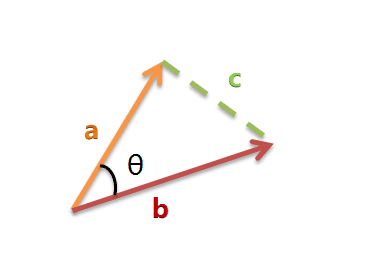
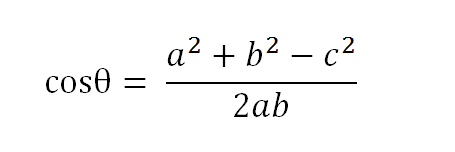
假定a向量是[x1,y1] 。b向量是 [x2,y2]
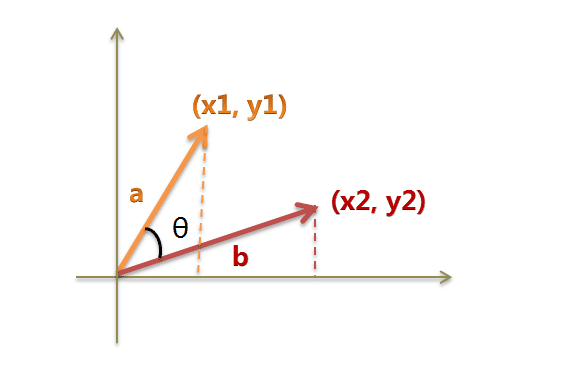
那么可以将余弦定理改成下面的形式。
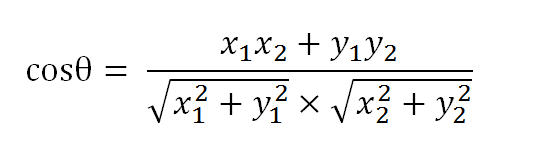
在原文中直接给了这个结果,这着实有点跳跃,给人以突兀感,主要是因为其中的推导过程给省略了,虽然推导过程确实有点小白,但我们的题目,就是将小白进行到底,所以还是在下面补出来这个过程。因为我不会画图所以直接使用计算机的表示法了。可能不太直观
Cosθ = (a^2+b^2-c^2)/2abc a^2 = (x1^2+y1^2) b^2 = (x2^2+y2^2) c^2 = (x2-x1)^2 + (y2-y1)^2 (这个不难理解吧) => Cosθ = ((x1^2+y1^2) + (x2^2+y2^2) + ((x2-x1)^2 + (y2-y1)^2))/(2sqrt(x1^2+y1^2)*sqrt(x2^2+y2^2)) => Cosθ = (x1^2+y1^2+x2^2+y2^2-x2^2-x1^2+2x1x2-y2^2-y1^2+2y1y2/(2sqrt(x1^2+y1^2)*sqrt(x2^2+y2^2)) => Cosθ = (2x1x2+y1y2 )/(2sqrt(x1^2+y1^2)*sqrt(x2^2+y2^2)) => Cosθ = (x1x2+y1y2 )/(sqrt(x1^2+y1^2)*sqrt(x2^2+y2^2))
这样结果就推出来了。
我们现在再来总结一下二维向量情况下余弦定理的规律
2个二维向量 [x1,y1] 、[x2,y2] 那么有
Cosθ = (x1x2+y1y2 )/(sqrt(x1^2+y1^2)*sqrt(x2^2+y2^2) )
我们把[x1,y1]、[x2,y2] 换成 [a1,a2] 、[b1,b2] 那么
有2个二维向量 [a1,a2] 、[b1,b2] 有
Cosθ = (a1b1+a2b2 )/(sqrt(a1^2+a2^2)*sqrt(b1^2+b2^2))
数学已经证明,余弦的这种计算扩展到多维向量也是成立的。
那么 现在我们多一个维度,假设有2个3维向量,例如 [a1,a2,a3]、[b1,b2,b3] 会是什么样呢
Cosθ = (a1b1+a2b2 +a3b3)/(sqrt(a1^2+a2^2+a3^2)*sqrt(b1^2+b2^2+b3^2))
那么 n维是什么情况呢
Cosθ = (a1b1+a2b2 +a3b3 + .. anbn)/(sqrt(a1^2+a2^2+a3^2 + ... + an^2)*sqrt(b1^2+b2^2+b3^2 + .. + bn^2))
下图的表示可能更直观和简洁一些
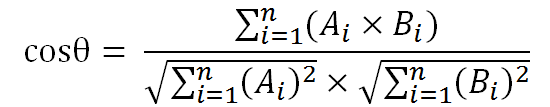
有了这个公式就好办了。我们的两个句子
句子A [1 , 2 , 0 , 2 , 1 , 1 , 0 , 1] 句子B [1 , 2 , 1 , 2 , 1 , 1 , 0 , 1]
那么他们夹角的余弦是多少呢
Cosθ = (1*1 + 2*2 + 0*1 + 2*2 + 1*1 + 1*1 + 0*0 + 1*1 )/(sqrt(1^2+2^2+0^2+2^2+1^2+1^2+0^2+1^2)*sqrt(1^2+2^2+1^2+2^2+1^2+1^2+1^2+0^2+1^2)) => Cosθ ≈0.961
这个还算是比较高的