机器学习实战笔记-5-Logistic回归

Logistic回归

优缺点	适用范围
优点：计算代价不高，易于理解和实现。 缺点：容易欠拟合，分类精度可能不高。 适用于：数值型和标称型数据。	仅用于二分类

原理：

每个特征都乘以一个回归系数>>将结果相加>>总和代入到Sigmoid函数，得到范围在(0,1)中的数值>>预测分类结果(hat{y})。即(Z= w_{0}x_{0} + w_{1}x_{1} + ldots + w_{n}x_{n} = sum_{i = 0}^{n}{w_{i}x_{i} =w^{T}x})，代入Sigmoid函数即可。
两个类别的分割点是(Z=0)，即直线(w_{0}x_{0}+w_{1}x_{1}+ldots +w_{n}x_{n}=0)。

[sigmaleft( Z ight) = frac{1}{1 + e^{- Z} } ightarrow y^{'} = frac{1}{1 + e^{- mathbf{w}^{T}mathbf{x} } } ext{ } frac{1}{1 + e^{gleft( x ight)} } ]

若用(y’)表示分类为1的概率，(Pleft( y = 1 middle| x,w ight) = y')，则分类为0的概率为(Pleft( y = 0 middle| x,w ight) = 1 - y')。

极大似然概率为(Lleft( w ight) = prod_{i = 1}^{m}{ { {(y}_{i}^{'})}^{y_{i} }left( 1 - y_{i}^{'} ight)^{1 - y_{i} } })，
取对数后为(mathbf{l}left( mathbf{w} ight)mathbf{=}sum_{mathbf{i = 1} }^{mathbf{m} }{mathbf{(}mathbf{y}_{mathbf{i} }logleft( mathbf{y}^{mathbf{'} } ight)mathbf{+ (1 -}mathbf{y}_{mathbf{i} }mathbf{)log(1 -}mathbf{y}_{mathbf{i} }^{mathbf{'} }mathbf{)} }mathbf{)})，迭代式为
(mathbf{w}_{mathbf{j} }mathbf{: =}mathbf{w}_{mathbf{j} }mathbf{+ alpha}frac{mathbf{partial} }{mathbf{partial}mathbf{w}_{mathbf{j} } }mathbf{l(w)})

[frac{partial}{partial w_{j} }lleft( w ight) = sum_{i = 1}^{m}{left( y_{i}frac{1}{y_{i}^{'} } + left( 1 - y_{i} ight)frac{1}{1 - y_{i}^{'} } ight)frac{partial}{partial w_{j} }y_{i}^{'} } = sum_{i = 1}^{m}{left( y_{i}frac{1}{y_{i}^{'} } + left( 1 - y_{i} ight)frac{1}{1 - y_{i}^{'} } ight)y_{i}^{'}left( 1 - y_{i}^{'} ight)frac{partial}{partial w_{j} }mathbf{w}^{T}mathbf{x} } ]

[= sum_{i = 1}^{m}{left( y_{i}left( 1 - y_{i}^{'} ight) + left( 1 - y_{i} ight)y_{i}^{'} ight)x_{i,j} } = sum_{mathbf{i = 1} }^{mathbf{m} }{mathbf{(}mathbf{y}_{mathbf{i} }mathbf{-}mathbf{y}_{mathbf{i} }^{mathbf{'} }mathbf{)} }mathbf{x}_{mathbf{i,j} } ]

其中用到了 记(fleft( x ight) = frac{1}{1 + e^{g(x)} })，则(frac{partial}{partial x}fleft( x ight) = fleft( x ight)left( 1 - fleft( x ight) ight)frac{partial}{partial x}g(x))

现有一数据集trainMat，记作矩阵X，则(error = mathbf{ ext{labelMat} } - sigma(mathbf{X} imes mathbf{w}))为预测值与实际值的差。

极大似然概率就是要回归的最大值(l(w))，并不在代码中体现，迭代式为

[w_{j} w_{j} + alphafrac{partial}{partial w_{j} }lleft( w ight) = w_{j} + alpha ullet sum_{mathbf{i = 1} }^{mathbf{m} }{mathbf{(}mathbf{y}_{mathbf{i} }mathbf{-}mathbf{y}_{mathbf{i} }^{mathbf{'} }mathbf{)} }mathbf{x}_{mathbf{i,j} } ]

[mathbf{w = w +}alphamathbf{ullet}mathbf{x}^{mathbf{T} }mathbf{ imes error} ]

梯度上升算法伪代码：

  每个回归系数初始化为1
  重复R次
    计算整个数据集的梯度
    使用alpha×gradient更新回归系数的向量
  返回回归系数

随机梯度上升算法伪代码：

每个回归系数初始化为1
对数据集中每个样本
  计算该样本的梯度
  使用alpha×gradient更新回归系数的值
返回回归系数值

---

知识点：最大似然估计法-本质就是求联合概率的最大值

二项分布的似然函数(某次实验：投n次硬币有m次正面)

[Lleft( heta ight) = C_{n}^{m} heta^{m}left( 1 - heta ight)^{n - m} ]

二项分布用通俗点的话来说，就是描述了抛10次硬币的结果的概率，其中，“花”出现的概率为( heta)。如{4,5,5,2,7,4}就是6次实验的结果，每个数字表示抛10次硬币出现了几次“花”。

用(x_{1},x_{2},ldots,x_{n})表示实验结果，则因为每次实验都是独立的，所以似然函数可以写作（得到这个似然函数很简单，独立事件的联合概率，直接相乘就可以得到）:

[Lleft( heta ight) = fleft( x_{1} middle| heta ight)fleft( x_{2} middle| heta ight)ldots fleft( x_{n} middle| heta ight) ]

其中(fleft( x_{n} middle| heta ight))表示同一参数下的实验结果，也可认为是条件概率。

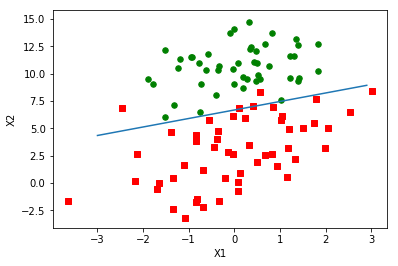
用python画的图