涵盖知识点:解析几何、树状数组
比赛链接:传送门
A - Alarm Clock
题意: 一天要睡够(a)分钟,但是(b)分钟后有一个闹钟会使其醒来,他会把闹钟推迟到(c)分钟之后,然后花费(d)小时再次入睡。问要多久能够睡够。
题解: 模拟推公式
Accept Code:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int main(){
int t;cin>>t;
while(t--){
ll a,b,c,d;
cin>>a>>b>>c>>d;
if(b>=a){
cout<<b<<"
";
continue;
}
if(d>=c){
cout<<-1<<"
";
continue;
}
cout<<(a-b+c-d-1)/(c-d)*c+b<<"
";
}
return 0;
}
B - Ternary String
题意: 给定的串仅含有(1,2,3)。问最短的字串使得同时存在这三种字符。
题解: 顺序扫描,在线更新。
Accept Code:
#include <bits/stdc++.h>
using namespace std;
int vis[3];
string s;
int main(){
int t;cin>>t;
while(t--){
memset(vis,0,sizeof vis);
cin>>s;
int ans=s.length()+1,n=0;
for(int i=0;i<s.length();i++){
while(n<s.length()&&(!vis[0]||!vis[1]||!vis[2])){
vis[s[n]-'1']++;
n++;
}
if(vis[0]&&vis[1]&&vis[2])ans=min(ans,n-i);
vis[s[i]-'1']--;
}
if(ans>s.length())cout<<"0
";
else cout<<ans<<"
";
}
return 0;
}
C1 - Simple Polygon Embedding
题意: (n)为偶数,(2n)个长度为(1)的线段构成一个正(2n)边形。问最小的正方形使得能够包裹住这个多边形。
题解: (2n)可被(4)整除。选两组对边与正方形重合显然最小。
Accept Code:
#include <bits/stdc++.h>
using namespace std;
const double pi=acos(-1);
int main(){
int t;cin>>t;
while(t--){
int n;
cin>>n;
printf("%.9lf
",1/tan(pi/(n*2)));
}
return 0;
}
C2 - Not So Simple Polygon Embedding
题意: n$为奇数,(2n)个长度为(1)的线段构成一个正(2n)边形。问最小的正方形使得能够包裹住这个多边形。
题解: 设偏转角为(x),外接圆半径为(l),所求正方形的半边长为(r),可以得出(r=l imes cos x),求导获得单调性(r'=-sin x)。在([0,pi])导数小于0,所以长度单调递减。又根据对称性可以得到取到的最小值应该在(x=frac{pi}{4n})时取到。
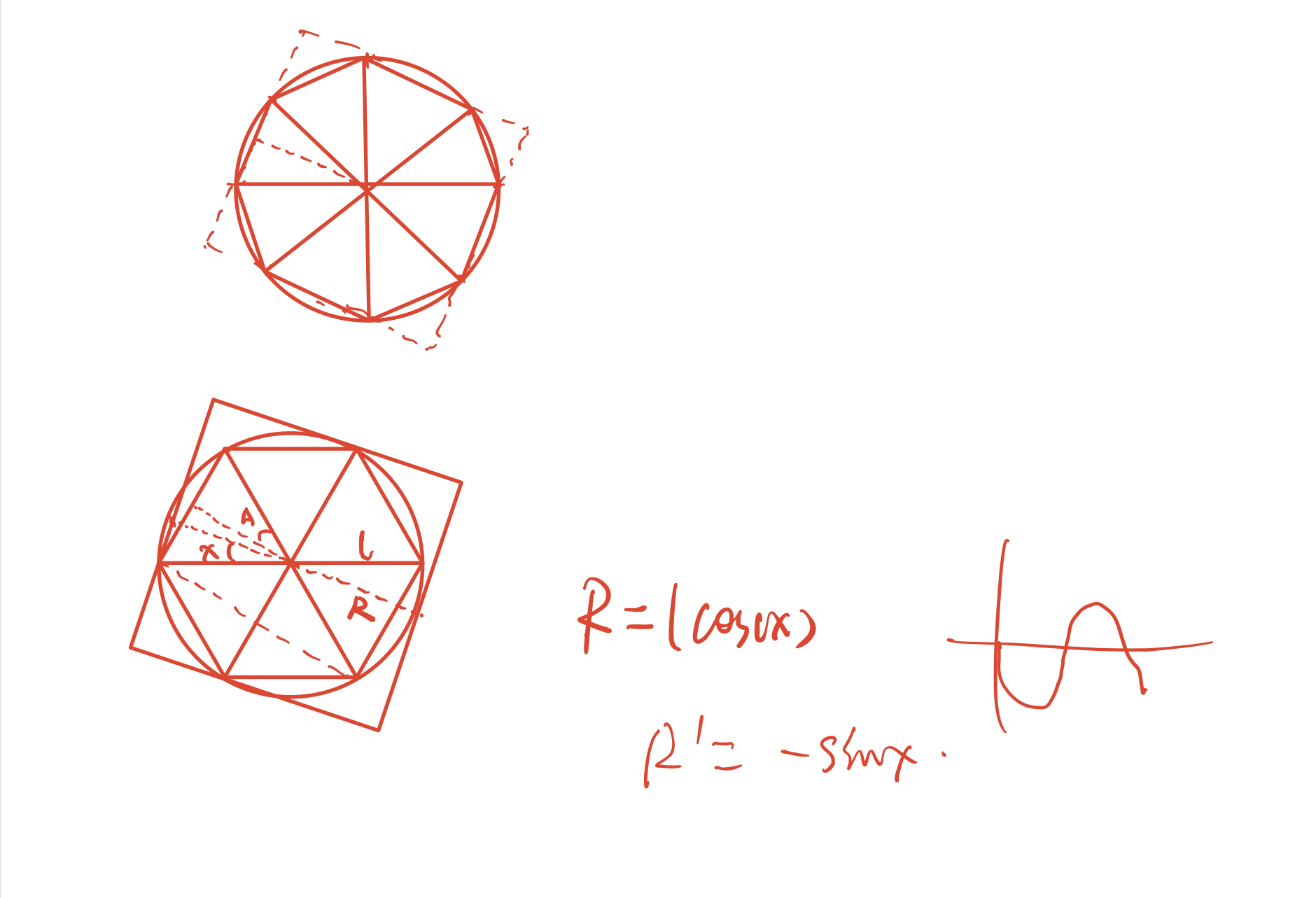
Accept Code:
#include <bits/stdc++.h>
using namespace std;
const double pi=acos(-1);
int main(){
int t;cin>>t;
while(t--){
int n;
cin>>n;
double a=pi/(n*2);
double r=1/sin(a);
a/=2;
printf("%.9lf
",r*cos(a));
}
return 0;
}
D - Multiset
题意: 多重集合,初始化后可以选择增加新数字或者删除某个位置的数字。求操作完成后集合内剩下的数字。
题解: 树状数组维护每个数字的个数。通过前缀和判断该位置是哪个数字。
Accept Code:
#include <bits/stdc++.h>
using namespace std;
const int maxn=1e6+10;
int c[maxn],n,q;
inline int lowbit(int x){return x&(-x);}
void add(int x){
while(x<=n){
c[x]++;
x+=lowbit(x);
}
}
void del(int x){
while(x<=n){
c[x]--;
x+=lowbit(x);
}
}
int query(int x){
int res=0;
while(x){
res+=c[x];
x-=lowbit(x);
}
return res;
}
int main(){
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
cin>>n>>q;
for(int i=0,x;i<n;i++)cin>>x,add(x);
for(int i=0,x;i<q;i++){
cin>>x;
if(x>0) { add(x); continue;}
x=-x;
int l=1,r=n,ans;
while(l<=r){
int mid=(l+r)/2;
if(query(mid)>=x)ans=mid,r=mid-1;
else l=mid+1;
}
del(ans);
}
for(int i=1;i<=n;i++){
if(query(i)){
cout<<i<<"
";
return 0;
}
}
cout<<"0
";
return 0;
}