Task异常捕获的方式

    这节来讲一下如何捕获Task的异常。

    当Task运行中出现了异常，正常情况下我们在主线程的Try是捕获不到的，而如果在Task内部写try，出现了异常我们会完全不知道。下面就来介绍几个主线程捕获Task异常的方法。

阻塞线程式

    我们可以使用Wait()，WaitAny()，WaitAll()来捕获Task的异常，详见下图：

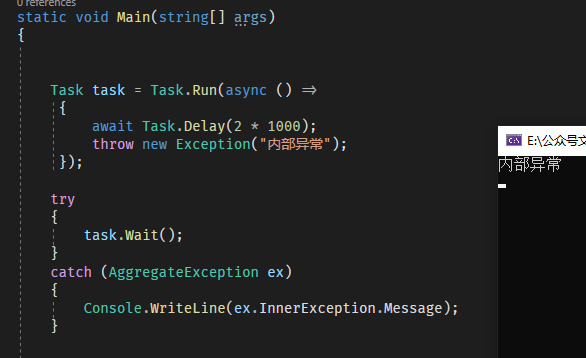
    捕获Task异常，准确来说要用AggregateException类，右边是运行结果，成功捕获到了异常信息，其它两个等待也是类似的用法，不熟悉的小伙伴可以参见前文：等待多个异步任务的方法。

    在等待多个Task异常时，可以访问异常对象的InnerExceptions属性来遍历所有的异常：

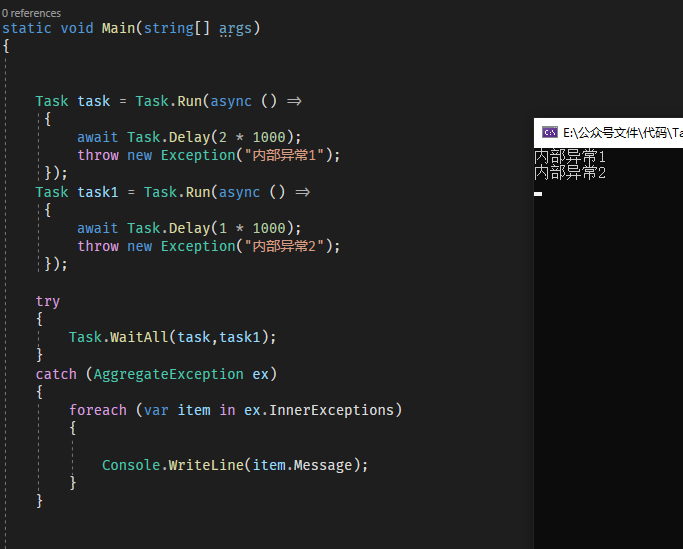
     上述异常捕获的解决方案，因为涉及到了等待，所以会阻塞主线程，并且如果异常发生在等待之前，同样是不能捕获到，所以这种方式，虽然简单，但是使用场景并不多。

异步式

    我们知道Task有个ContinueWith方法，它会在Task完成后继续异步执行传入的委托，我们可以通过这个方法实现异常捕获，请看如下代码：

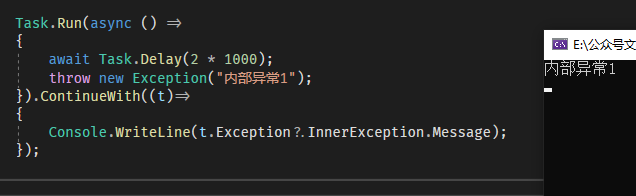
    因为是异步执行，所以这样不会阻塞主线程。

事件式

    事件式的思路是在主线程中定义事件，在Task中通过触发事件的形式让主线程捕获到异常，请看代码：

    首先定义一个事件参数：

internal class TaskExceptionEventArgs:EventArgs
{
    /// <summary>
    /// 存放Task引发的异常对象
    /// </summary>
    public AggregateException AggregateException { get; set; }  
}

    主代码如下：

class Program
{
    private static event EventHandler<TaskExceptionEventArgs> taskExceptionEventHandler;
    static void Main(string[] args)
    {
        //为事件添加事件处理器
        taskExceptionEventHandler = (sender, aeArgs) =>
        {
            Console.WriteLine(aeArgs.AggregateException.Message);
        };
        Task.Run(async () =>
        {
            await Task.Delay(2 * 1000);
            try
            {
                throw new AggregateException("内部异常1");
            }
            catch (AggregateException ex)
            {
                //触发事件，并传入参数
                taskExceptionEventHandler.Invoke(null, new TaskExceptionEventArgs
                {
                    AggregateException = ex
                });
            }
        });
    }
}

这样用法很灵活，而且拿到的是最直接的异常对象，并且不用等待Task执行完毕。