[LOJ3066]\[ROI 2016]快递

[LOJ3066][ROI 2016]快递

（找不到题解，看了别人代码，自己理解了一下）

题意：给定一些路径，求最长的相交长度-1，并且输出方案

(注意没有相交时输出0而不是-1)

明显的结论：两条路径的 相交路径的LCA一定是某一条路径的LCA

暴力：我们可以通过求若干次LCA来得到一对路径的答案，枚举+RMQ求LCA就能做到\(O(n^2)\)

一、对于相交路径为单链的情况：

我们可以通过从每条路径的\(LCA\)向下二分找到最长的单链存在另一条路径包含它，这个可以用一些奇怪的数据结构(主席树)求出

#include<bits/stdc++.h>

using namespace std;

#define reg register
typedef long long ll;
#define rep(i,a,b) for(reg int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(reg int i=a,i##end=b;i>=i##end;--i)

#define pb push_back
template <class T> inline void cmin(T &a,T b){ if(a>b) a=b; }
template <class T> inline void cmax(T &a,T b){ if(a<b) a=b; }

char IO;
template <class T=int> T rd(){
	T s=0;
	int f=0;
	while(!isdigit(IO=getchar())) if(IO=='-') f=1;
	do s=(s<<1)+(s<<3)+(IO^'0');
	while(isdigit(IO=getchar()));
	return f?-s:s;
}


const int N=2e5+10,K=30;

int n,m;
vector <int> G[N];
int a[N],b[N],lca[N],dep[N],fa[N][20];

int L[N],R[N],id[N],dfn;
void dfs(int u,int f) {
	id[L[u]=++dfn]=u;
	fa[u][0]=f;
	rep(i,1,18) fa[u][i]=fa[fa[u][i-1]][i-1];
	for(int v:G[u]) if(v!=f) {
		dep[v]=dep[u]+1;
		dfs(v,u);
	}
	R[u]=dfn;
}

int Up(int x,int k) {
	for(reg int i=0;(1<<i)<=k;++i) if(k&(1<<i)) x=fa[x][i];
	return x;
}

int LCA(int x,int y) {
	if(dep[x]<dep[y]) swap(x,y);
	x=Up(x,dep[x]-dep[y]);
	if(x==y) return x;
	drep(i,18,0) if(fa[x][i]!=fa[y][i]) x=fa[x][i],y=fa[y][i];
	return fa[x][0];
}

vector <int> U[N];
int rt[N],cnt;
int ls[N*K],rs[N*K],s[N*K];
void Upd(int &p,int pre,int l,int r,int x) {
	p=++cnt;
	s[p]=s[pre]+1,ls[p]=ls[pre],rs[p]=rs[pre];
	if(l==r) return;
	int mid=(l+r)>>1;
	x<=mid?Upd(ls[p],ls[pre],l,mid,x):Upd(rs[p],rs[pre],mid+1,r,x);
}

int Que(int pl,int pr,int l,int r,int ql,int qr) {
	if(ql>qr) return 0;
	if(l==ql && r==qr) return s[pr]-s[pl];
	int mid=(l+r)>>1;
	if(qr<=mid) return Que(ls[pl],ls[pr],l,mid,ql,qr);
	else if(ql>mid) return Que(rs[pl],rs[pr],mid+1,r,ql,qr);
	else return Que(ls[pl],ls[pr],l,mid,ql,mid)+Que(rs[pl],rs[pr],mid+1,r,mid+1,qr);
}

int Get(int x,int y){
	if(dep[x]>dep[y]) swap(x,y);
	if(x!=y) {
		int t=Up(y,dep[y]-dep[x]-1);
		return Que(rt[0],rt[L[t]-1],1,n,L[y],R[y])+Que(rt[L[y]-1],rt[R[y]],1,n,R[t]+1,n);
	} else return Que(rt[0],rt[L[x]],1,n,L[y],R[y])+Que(rt[L[y]-1],rt[R[y]],1,n,R[x]+1,n);
}

int lst;

int Check(int mid) {
	rep(i,1,m) {
		if(dep[a[i]]-dep[lca[i]]>=mid) {
			int t=Up(a[i],dep[a[i]]-dep[lca[i]]-mid);
			if(Get(lca[i],t)>=2) {
				lst=i;
				return 1;
			}
		}
		if(dep[b[i]]-dep[lca[i]]>=mid) {
			int t=Up(b[i],dep[b[i]]-dep[lca[i]]-mid);
			if(Get(lca[i],t)>=2) {
				lst=i;
				return 1;
			}
		}
	}
	return 0;
}


namespace pt1{
	int Get(int a,int b,int c,int d) {
		return max(0,dep[LCA(b,d)]-max(dep[a],dep[c]));
	}
	int Ans(int i,int j){
		int x=LCA(a[i],b[i]),y=LCA(a[j],b[j]);
		int t=Get(x,a[i],y,a[j])+Get(x,a[i],y,b[j])+Get(x,b[i],y,a[j])+Get(x,b[i],y,b[j]);
		return t;
	}
}

int main(){
	n=rd(),m=rd();
	rep(i,2,n) {
		int f=rd();
		G[f].pb((int)i),G[i].pb(f);
	}
	dfs(1,0);
	rep(i,1,m) {
		a[i]=rd(),b[i]=rd();
		lca[i]=LCA(a[i],b[i]);
		int x=L[a[i]],y=L[b[i]];
		if(x>y) swap(x,y);
		U[x].pb(y);
	}
	rep(i,1,n) {
		rt[i]=rt[i-1];
		for(int j:U[i]) Upd(rt[i],rt[i],1,n,j);
	}
	int l=1,r=n,res=0;
	while(l<=r) {
		int mid=(l+r)>>1;
		if(Check(mid)) l=mid+1,res=mid;
		else r=mid-1;
	}
	printf("%d\n",res);
	if(res==0) {
		puts("1 2");
		return 0;
	}
	rep(i,1,m) if(i!=lst) {
		if(pt1::Ans(lst,i)>=res) {
			printf("%d %d\n",lst,i);
			return 0;
		}
	}
}

\[\ \]

\[\ \]

二、对于相交路径是两条垂下来的链的情况

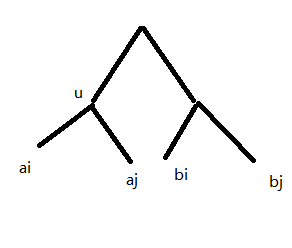
我们通过差分的方式在一个端点加入另一个端点

通过启发式合并转移到儿子

接下来我们考虑合并时的贡献

那么\(a_i\)，\(a_j\)在\(u\)处产生第一次合并，我们就知道答案是\(dep[u]+dep[LCA(b_i,b_j)]-dep[LCA(a_i,b_i)]\cdot 2\)

可以看到，只与\(dep[LCA(b_i,b_j)]\)有关

显然我们不能直接枚举，于是考虑插入\(b_i\)时，只与欧拉序最靠近的两个\(b_j\)产生计算，模拟\(RMQ\)求\(LCA\)可以知道，这样的\(dep[LCA(b_i,b_j)]\)才有可能是最大的

由于需要找前驱后继，所以直接用\(set\)维护合并比较方便

#include<bits/stdc++.h>

using namespace std;

#define reg register
typedef long long ll;
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)

#define pb push_back
template <class T> inline void cmin(T &a,T b){ if(a>b) a=b; }
template <class T> inline void cmax(T &a,T b){ if(a<b) a=b; }

char IO;
template <class T=int> T rd(){
	T s=0;
	int f=0;
	while(!isdigit(IO=getchar())) if(IO=='-') f=1;
	do s=(s<<1)+(s<<3)+(IO^'0');
	while(isdigit(IO=getchar()));
	return f?-s:s;
}


const int N=2e5+10;

int n,m;
vector <int> G[N];
int a[N],b[N];

int line[N<<1],pos[N],lc,Log[N<<1],dep[N];
int s[20][N<<1];

void dfs(int u,int f) {
	line[pos[u]=++lc]=u;
	for(int v:G[u]) if(v!=f) {
		dep[v]=dep[u]+1,dfs(v,u);
		line[++lc]=u;
	}
}

void PreMake(){
	rep(i,2,lc) Log[i]=Log[i>>1]+1;
	rep(i,1,lc) s[0][i]=line[i];
	rep(i,1,Log[lc]) {
		int len=1<<(i-1);
		rep(j,1,lc+1-(1<<i)) {
			s[i][j]=dep[s[i-1][j]]<dep[s[i-1][j+len]]?s[i-1][j]:s[i-1][j+len];
		}
	}
}
int LCA(int x,int y) {
	x=pos[x],y=pos[y];
	if(x>y) swap(x,y);
	int d=Log[y-x+1];
	return dep[s[d][x]]<dep[s[d][y-(1<<d)+1]]?s[d][x]:s[d][y-(1<<d)+1];
}

struct Node{
	int x,y;
	bool operator < (const Node __) const {
		return x!=__.x?pos[x]<pos[__.x]:y<__.y;
	}
};

set <Node> S[N];
vector <Node> Add[N],Del[N];
int ans,ansx=1,ansy=2;

int Get(int a,int b,int c,int d) {
	return max(0,dep[LCA(b,d)]-max(dep[a],dep[c]));
}
void Upd_Ans(int i,int j) {
	if(i==j) return;
	int x=LCA(a[i],b[i]),y=LCA(a[j],b[j]);
	int t=Get(x,a[i],y,a[j])+Get(x,a[i],y,b[j])+Get(x,b[i],y,a[j])+Get(x,b[i],y,b[j]);
	if(t>ans) ans=t,ansx=i,ansy=j;
}

typedef set <Node> ::iterator iter;
void Insert(int u,Node x){
	iter it=S[u].lower_bound(x);
	if(it!=S[u].end()) Upd_Ans(x.y,it->y);
	if(it!=S[u].begin()) Upd_Ans(x.y,(--it)->y);
	S[u].insert(x);
}

void dfs_getans(int u,int f) {
	for(int v:G[u]) if(v!=f) {
		dfs_getans(v,u);
		if(S[v].size()>S[u].size()) swap(S[u],S[v]);
		for(Node i:S[v]) Insert(u,i);
	}
	for(Node i:Add[u]) Insert(u,i);
	for(Node i:Del[u]) S[u].erase(i);
}



int main(){
	n=rd(),m=rd();
	rep(i,2,n) {
		int f=rd();
		G[i].pb(f),G[f].pb(i);
	}
	dfs(1,0),PreMake();
	rep(i,1,m) {
		a[i]=rd(),b[i]=rd();
		int lca=LCA(a[i],b[i]);
		Add[a[i]].pb((Node){b[i],i}),Add[b[i]].pb((Node){a[i],i});
		Del[lca].pb((Node){b[i],i}),Del[lca].pb((Node){a[i],i});
	}
	dfs_getans(1,0);
	printf("%d\n%d %d\n",ans,ansx,ansy);
}