字符串的Period(周期),Border

字符串的Period(周期),Border

前置知识：( ext{kmp})，( ext{AC})自动机

约定：字符串(S)的长度为(|S|)，原串的长度为(n)，([l,r])的子串为(S_{l,r})，下标从(1)开始，前缀(S_{1,i}=pre_i),后缀(S_{i,n}=suf_i)，设(S)的( ext{Border})集合为(B(S))，设最长的( ext{Border})为( ext{LBorder})

( ext{Border}):

定义字符串(S)的一个( ext{Border})为一个满足(pre_i=suf_{n-i+1})的前缀，(S)和(empty)也是一个( ext{Border})

( ext{kmp,AC})自动机的(fail)指针均指向当前串的( ext{LBorder})

[ ]

( ext{Period})(周期):

若(exists |T|in B(S), 2|T|ge n),则(S)的一个周期是(n-|T|+1)

( ext{Periodicity Lemma}:)

若(p,q)是(S)的周期，且(p+q+gcd(p,q)leq |S|),则(gcd(p,q))也是(|S|)的一个周期

证明的话

[ ]

关于( ext{Border})的推论:

1.(B(S)=B( ext{LBorder})cup{S})

2.串(S)的所有( ext{Border})长度构成了不超过(log n)个等差数列

证明：

如果(S)的( ext{LBorder})，设其为(T)满足(2|T|ge |S|)，则所有(Rin B(S),2|R|ge |S|)形成了一个等差数列

参过下面这张图

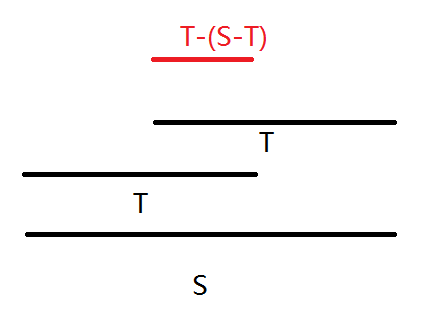
则长度为(|T|-(|S|-|T|))，即标为红色的那一段，它也是原串的一个( ext{Border})

更简洁的解释是，(S)有着长度为(|S|-|T|)的周期

所以实际上不止是(2|R|ge |S|)的串，而是所有(forall|R|equiv |S|pmod {|S|-|T|})的(R)都是(S)的( ext{Border})

这样的失配过程就可以归纳为：

每次(mod)最短周期(|T|-|S|)，而取模使得长度至少减半，故可以分成(log n)段等差数列

[ ]

并且任意一段最大项为(x)，差为(d)的等差数列，最小项是(xmod d+d)

((+d)是因为在(xmod d+d)下一次可能跳的位置(>xmod d))

应用：对于( ext{kmp,AC})自动机的字符集过大导致无法存储每种字符的转移，而又有类似可持久化的匹配操作时，

直接暴力跳(fail)会导致复杂度退化，但是可以用等差数列的性质来快速跳

每次形成等差数列时，周期中失配位置的下一个字符都相同

故如果在等差数列上失配，可以直接通过对于差值取模快速跳过，以保证复杂度为(O(log n))

相比于倍增处理，这样跳常数小，实现简单

具体看下面的习题代码

练习模板: Luogu P5829 求公共( ext{Border})

#include<bits/stdc++.h>
using namespace std;
enum{N=1000010};
char s[N];
int _,i,j,nxt[N];
int main(){
	for(scanf("%s",s+1),i=2;s[i];++i){
		while(j && s[i]!=s[j+1]) j=nxt[j];
		if(s[i]==s[j+1]) j++;
		nxt[i]=j;
	}
	for(scanf("%d",&_);_--;){
		for(scanf("%d%d",&i,&j),i=nxt[i],j=nxt[j];i!=j;){
			if(i<j) swap(i,j);
			if(nxt[i]>i/2) {
                // 产生等差数列，快速跳过
				int d=i-nxt[i];
				if(j%d==i%d) i=j;
				else i=i%d+d;
			} else i=nxt[i];
		}
		printf("%d
",i);
	}
}