「ROI 2018 Day 1」量子隐形传态
题目大意:
在(N imes M)的网格上给定(K)个点(1ldots K),定义两点间的距离为(displaystyle 2^{max{|x_i-x_j|,|y_i-y_j|}})
(N,M,Kleq 10^4),求(1)到(k)的最短路,下文认为(N,M)同阶
如何存储距离
显然距离是一个不超过(10^4)位的二进制数,用( ext{bitset})存下来
每一次转移需要维护一个位+1操作,比较大小操作,都可以(O(frac{N}{w}))实现,其中( ext{w})为压位数
[
]
Lemma:
对于点(A(x,y)),将平面分为(8)个部分
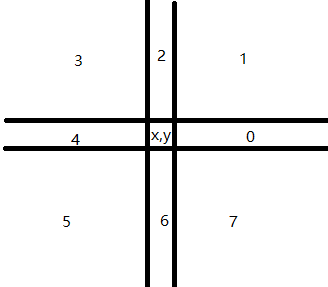
注意对于(x'=x)或者(y'=y)的区域一定要分离
则有:在任意一个平面区域中,有效的转移点一定是距离((x,y))最近的点
简要证明:
对于(A)来说,切比雪夫距离相同的的点构成一条带
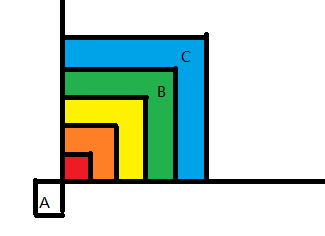
设最近的点为(B),那么对于任意一个其它点(C),显然有(dis(A,C)>dis(B,C),dis(A,C)>dis(A,B))
故走(A ightarrow B ightarrow C)不劣
快速完成转移
这样的(B)显然不唯一存在,每次转移需要的是( ext{L})形的段
故可以对于每行每列用线段树优化区间连边
故得到一个(O(K))点数,(O(Klog K))边数的图
用( ext{Dijkstra})完成最短路,复杂度为(O(Klog ^2 Kfrac{N}{W}))
ps: 这里没有考虑找到最近点的过程 ,下面的代码是直接暴力找的。。。
#include<bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
typedef pair <int,int> Pii;
#define reg register
#define pb push_back
#define mp make_pair
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
#define drep(i,a,b) for(int i=a,i##end=b;i>=i##end;--i)
template <class T> inline void cmin(T &a,const T &b){ ((a>b)&&(a=b)); }
template <class T> inline void cmax(T &a,const T &b){ ((a<b)&&(a=b)); }
char IO;
int rd(){
int s=0;
while(!isdigit(IO=getchar()));
do s=(s<<1)+(s<<3)+(IO^'0');
while(isdigit(IO=getchar()));
return s;
}
const int N=30011,INF=1e9+10,U=10000,D=6;
bool Mbe;
int n,m,k;
int X[N],Y[N],pre[N],vis[N];
vector <Pii> E[N];
typedef unsigned long long ull;
struct Bitset{
ull a[N/64+10];
int l;
void Add(int x){
while(1) {
ull t=a[x>>D];
a[x>>D]+=1ull<<(x&63);
if(t>a[x>>D]) x=((x>>D)+1)<<D;
else break;
}
cmax(l,((x>>D)<<D)+63-__builtin_clzll(a[x>>D]));
}
bool operator < (const Bitset &__) const {
if(__.l>10009) return 1;
if(l!=__.l) return l<__.l;
drep(i,(l>>D)+1,0) if(a[i]!=__.a[i]) return a[i]<__.a[i];
return 0;
}
} dis[N];
struct Queue{
int s[N<<2],bit;
void Up(int p) { s[p]=dis[s[p<<1]]<dis[s[p<<1|1]]?s[p<<1]:s[p<<1|1]; }
void Build(){
for(bit=1;bit<=n+1;bit<<=1);
s[bit+1]=1;
for(int p=bit+1;p;p>>=1) s[p]=1;
}
void push(int p) { for(s[p+bit]=p,p+=bit;p>>=1;) Up(p); }
int top(){
int res=s[1],p=s[1];
for(s[p+=bit]=0;p>>=1;) Up(p);
return res;
}
} que;
int Dis(int x,int y) { return max(abs(X[x]-X[y]),abs(Y[x]-Y[y])); }
int Ans[N],Ac;
int Min[N][8];
int Dir(int u,int v){
int x=X[v]-X[u],y=Y[v]-Y[u];
if(y==0) return x>0?0:4;
if(y>0) return x==0?2:(x>0?1:3);
return x==0?6:(x>0?7:5);
}
typedef vector <int> V;
V A[N],B[N];
int rtx[N],rty[N],ls[N],rs[N];
int Build(const V &vec,int l,int r){
if(l==r) return vec[l];
int mid=(l+r)>>1,u=++n;
ls[u]=Build(vec,l,mid),rs[u]=Build(vec,mid+1,r);
E[u].pb(mp(ls[u],-1)),E[u].pb(mp(rs[u],-1));
return u;
}
V Res;
void Que(const V &vec,int p,int l,int r,int ql,int qr){
if(!p) return;
if(ql<=vec[l] && vec[r]<=qr) return Res.pb(p);
int mid=(l+r)>>1;
if(ql<=vec[mid]) Que(vec,ls[p],l,mid,ql,qr);
if(qr>=vec[mid+1]) Que(vec,rs[p],mid+1,r,ql,qr);
}
void AddX(int u,int x,int l,int r){
int d=abs(x-X[u]);
if(rtx[x]) Que(A[x],rtx[x],0,A[x].size()-1,l,r);
for(int v:Res) {
E[u].pb(mp(v,d));
}
Res.clear();
}
void AddY(int u,int y,int l,int r){
int d=abs(y-Y[u]);
if(rty[y]) Que(B[y],rty[y],0,B[y].size()-1,l,r);
for(int v:Res) {
E[u].pb(mp(v,d));
}
Res.clear();
}
void Init(){
rep(i,1,k) A[X[i]].pb(i),B[Y[i]].pb(i);
rep(i,1,U) {
if(A[i].size()) {
sort(A[i].begin(),A[i].end(),[&](int x,int y){ return Y[x]<Y[y]; });
rtx[i]=Build(A[i],0,A[i].size()-1);
for(int &j:A[i]) j=Y[j];
}
if(B[i].size()) {
sort(B[i].begin(),B[i].end(),[&](int x,int y){ return X[x]<X[y]; });
rty[i]=Build(B[i],0,B[i].size()-1);
for(int &j:B[i]) j=X[j];
}
}
rep(i,1,k) rep(j,0,7) Min[i][j]=INF;
rep(i,1,k) rep(j,i+1,k){
int d=Dir(i,j),dis=Dis(i,j);
cmin(Min[i][d],dis);
cmin(Min[j][(d+4)&7],dis);
}
rep(i,1,k) {
if(Min[i][0]!=INF) AddX(i,X[i]+Min[i][0],Y[i],Y[i]);
if(Min[i][1]!=INF) {
AddX(i,X[i]+Min[i][1],Y[i]+1,Y[i]+Min[i][1]);
AddY(i,Y[i]+Min[i][1],X[i]+1,X[i]+Min[i][1]);
}
if(Min[i][2]!=INF) AddY(i,Y[i]+Min[i][2],X[i],X[i]);
if(Min[i][3]!=INF) {
AddX(i,X[i]-Min[i][3],Y[i]+1,Y[i]+Min[i][3]);
AddY(i,Y[i]+Min[i][3],X[i]-Min[i][3],X[i]-1);
}
if(Min[i][4]!=INF) AddX(i,X[i]-Min[i][4],Y[i],Y[i]);
if(Min[i][5]!=INF) {
AddX(i,X[i]-Min[i][5],Y[i]-Min[i][5],Y[i]-1);
AddY(i,Y[i]-Min[i][5],X[i]-Min[i][5],X[i]-1);
}
if(Min[i][6]!=INF) AddY(i,Y[i]-Min[i][6],X[i],X[i]);
if(Min[i][7]!=INF) {
AddX(i,X[i]+Min[i][7],Y[i]-Min[i][7],Y[i]-1);
AddY(i,Y[i]-Min[i][7],X[i]+1,X[i]+Min[i][7]);
}
}
}
bool Med;
int main(){
fprintf(stderr,"%.2lf
",(&Med-&Mbe)/1024.0/1024.0);
n=rd(),m=rd(),k=rd(),n=k;
rep(i,1,k) X[i]=rd(),Y[i]=rd();
Init();
que.Build();
dis[0].Add(10111);
rep(i,2,n) dis[i].Add(10110);
while(que.s[1]) {
int u=que.top();
vis[u]=1;
for(auto t:E[u]) {
int v=t.first;
Bitset w=dis[u]; if(~t.second) w.Add(t.second);
if(w<dis[v]) dis[v]=w,que.push(v),pre[v]=u;
}
}
for(int u=k;u;u=pre[u]) if(u<=k) Ans[++Ac]=u;
printf("%d
",Ac);
drep(i,Ac,1) printf("%d ",Ans[i]);
}