「ROI 2016 Day1」人烟之山

「ROI 2016 Day1」人烟之山

题目大意：

有(n)段折线，(m)个查询点(A)（在折线以上），设折线拐点为(X_i)

求折线上在查询点投影两边最近的位置(B)，且直线(AB)与折线有非边缘的交点 (即从(A)点看过来会被折线遮住)

题目分析：

(B,C)点满足的条件就是其旁边的直线(L)在(x_A)处的值(>y_A)

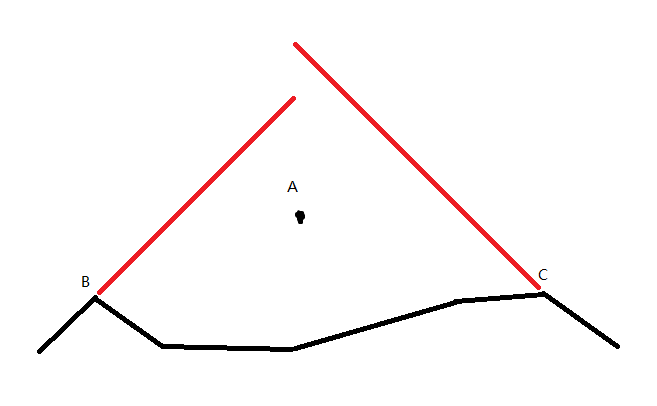
即找到最近的红色直线

Solution1 (O(nlog ^2n))

以求左边为例

考虑二分答案，求出拐点为(X_i,ige mid)的直线中是否存在红色直线

也就是求最大值是否(>y_A)，维护直线最大值，并且区间查询，可以暴力可持久化李超树来解决

因为是求左边的，所以每条直线更新的范围(>X_i)，李超树区间更新复杂度为(O(log ^2n))

李超树查询复杂度为(O(log n)),加上二分，查询为(O(log ^2n))

[ ]

Solution2 (O(nlog n))

依然考虑二分，但是这次考虑在线段树上二分

对于所有的(X_i)建立线段树，区间([L,R])内维护一个(X_i,iin [L,R])的上凸包，静态维护最大值

凸包可以归并子节点来建立，预处理复杂度为(O(nlog n))

如果查询直接在凸包上二分，复杂度会增加一个(log n)

解决方法是：将所有查询的(x_A)排序，然后在凸包上查询时就可以做到线性

因此复杂度为(O(nlog n))

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
typedef double db;
#define pb push_back
#define rep(i,a,b) for(int i=a,i##end=b;i<=i##end;++i)
char buf[200000],*p1,*p2;
#define getchar() (((p1==p2)&&(p2=(p1=buf)+fread(buf,1,200000,stdin))),*p1++)
char IO;
int rd(){
	int s=0; int f=0;
	while(!isdigit(IO=getchar())) f|=IO=='-';
	do s=(s<<1)+(s<<3)+(IO^'0');
	while(isdigit(IO=getchar()));
	return f?-s:s;
}

const int N=4e5+10,U=1e9+10;

int n,m,K[N],X[N],L[N],R[N];
ll Y[N];
struct Que{
	int x,y,id;
	bool operator < (const Que __) const {
		return x<__.x;
	}
} Q[N];
struct Node{
	int k; ll b;
	ll operator [] (const ll x) const {
		return 1ll*k*x+b;
	}
	friend db Cross(Node x,Node y){ return 1.0*(y.b-x.b)/(x.k-y.k); }
	bool operator < (const Node __) const {
		return k<__.k||(k==__.k && b<__.b);
	}
}; 
vector <Node> H[N<<2];
vector <Node> ::iterator P[N<<2];
void Build(int p,int l,int r){
	if(l==r) return H[p].pb((Node){K[l],Y[l]-1ll*K[l]*X[l]}),P[p]=H[p].begin(),void();
	int mid=(l+r)>>1;
	Build(p<<1,l,mid),Build(p<<1|1,mid+1,r);
	int p1=0,s1=H[p<<1].size(),p2=0,s2=H[p<<1|1].size(),R=-1;
	auto Ins=[&](Node L) {
		while(~R && H[p][R].b<=L.b) R--,H[p].pop_back();
		while(R>0 && Cross(H[p][R],H[p][R-1])>=Cross(H[p][R],L)-1e-8) R--,H[p].pop_back();
		H[p].pb(L),R++;
	};
	while(p1<s1 || p2<s2) {
		if(p1<s1 && (p2==s2 || H[p<<1][p1]<H[p<<1|1][p2])) Ins(H[p<<1][p1++]);
		else Ins(H[p<<1|1][p2++]);
	}
	P[p]=H[p].begin();
}

ll Que(int p,int x){
	while(P[p]+1!=H[p].end() && (*(P[p]+1))[x]>=(*P[p])[x]) P[p]++;
	return (*P[p])[x];
}
int QueL(int p,int l,int r,int x,int qx,int y){
	if(x<l || Que(p,qx)<=y) return 0;
	if(l==r) return l;
	int mid=(l+r)>>1,t;
	if(x>mid && (t=QueL(p<<1|1,mid+1,r,x,qx,y))) return t;
	return QueL(p<<1,l,mid,x,qx,y);
}
int QueR(int p,int l,int r,int x,int qx,int y){
	if(x>r || Que(p,qx)<=y) return n+1;
	if(l==r) return l;
	int mid=(l+r)>>1,t;
	if(x<=mid && (t=QueR(p<<1,l,mid,x,qx,y))<=n) return t;
	return QueR(p<<1|1,mid+1,r,x,qx,y);
}

int main(){
	n=rd(),m=rd();
	rep(i,1,n) {
		X[i]=X[i-1]+rd(),K[i]=rd();
		Y[i]=Y[i-1]+1ll*(X[i]-X[i-1])*K[i];
	}
	rep(i,1,m) Q[i].x=rd(),Q[i].y=rd(),Q[i].id=i;
	sort(Q+1,Q+m+1);
	Build(1,1,n);
	int p=1;
	rep(i,1,m) {
		while(p<=n && X[p]<Q[i].x) p++;
		L[Q[i].id]=QueL(1,1,n,p-1,Q[i].x,Q[i].y);
		R[Q[i].id]=QueR(1,1,n,p+(X[p]==Q[i].x),Q[i].x,Q[i].y);
	}
	rep(i,1,m) printf("%d %d
",X[L[i]],X[R[i]-1]);
}