python计算置信区间

python 置信区间

置信区间是指由 样本统计量 所构造的总体参数的估计区间。
这句话也就是说 ( 这里统计量一般指均值 ) 利用样本均值来估计总体均值的可靠程度, 这个"可靠程度"用"置信区间"来表示, 置信区间(是一个系数)取值范围为: 0<置信区间<1; 这个置信区间就是用来描述真实的均值发生在某范围的概率
当样本量越大, 则越可靠.

置信区间计算公式:

ci = mean±stdN(ppf)( (1-α)/2 )
公式参数说明:
ci: 表示置信区间
mean: 表示样本均值
std: 表示样本标准差
N(ppf): 表示正态分布的百分点函数
α : 是显著性水平
α的取值跟样本量有关

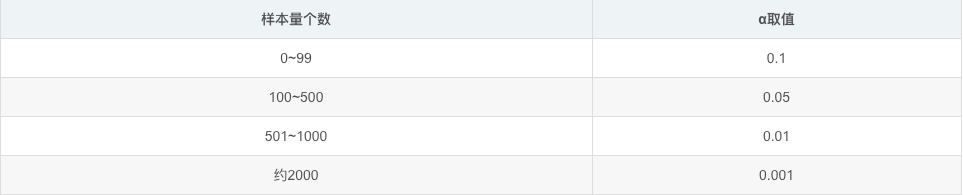
其中，百分点函数ppf是累积分布函数cdf的反函数

常用的几个置信区间的计算可以不用上述公式,而使用更简单的公式

置信水平是指特定个体对待特定命题真实性相信的程度
通常使用 90%，95% 和 99% 作为置信区间的置信水平。这三个置信水平的临界值分别为 1.64，1.98 和 2.32。
se是样本标准误, n是样本个数
se = mean/pow(n,0.5)

置信区间算法:
ci = mean-se1.64 置信水平为0.9
ci = mean-se1.98 置信水平为0.95
ci = mean-se*2.32 置信水平为0.99

举例来说，如果在一次大选中某人的支持率为55%，而置信水平(也称为可信区间)0.95以上的置信区间是(50%,60%)，那么他的真实支持率有百分之九十五的机率落在百分之五十和百分之六十之间，因此他的真实支持率不足一半的可能性小于百分之2.5。 如例子中一样，置信水平一般用百分比表示，因此置信水平0.95上的置信空间也可以表达为:95%置信区间。置信区间的两端被称为置信极限。对一个给定情形的估计来说，显著性水平越高，所对应的置信区间就会越大。

但是; 重点来了, 在python里可以直接调用函数求出置信区间

置信水平 = 可信区间 = 可信度 ;他们是同一个说法(其中可信度是为了方便理解,在案例中我用于替代置信水平的)

置信区间宽度 = 置信区间上极限 - 置信区间下极限
结论是:置信区间宽度越小,预测模型越精确;但是置信区间宽度小了,可信度也就越小了

"""  置信区间  """
 
    df = len(data) - 1
    alpha=    # 是设定的可信区间, 可以理解为可信度; 数值是百分数,取值范围(0,1)
    ci = stats.t.interval(alpha, df, loc=np.mean(data), scale=stats.sem(data)) # ci是置信区间

　　

案例: 对给出的样本数据分析(所用文件是csv格式的,无法导入)

import os
import pandas as pd
import matplotlib
import matplotlib.pyplot as plt
from scipy import stats
import numpy as np

os.chdir(r"D:python金融")
data = pd.read_csv("house_price_gr.csv",encoding='gbk') # 文件有中文,encoding= 'gbk'

matplotlib.rcParams['axes.unicode_minus']=False#解决保存图像时负号'-'显示为方块的问题
plt.rcParams['font.sans-serif'] = ['SimHei'] # 指定默认字体

# print(data.shape[0]) # 查看样本数量

# 绘制直方图 plt.hist(样本数据,bins=柱子个数) ; 默认x轴是样本数值, y轴是样本数值的个数
# plt.hist(data.rate,bins=40)
# plt.show()

# 查看均值,标准差,百分位数等
print(data.rate.describe())

alpha = 0.99
alpha_list = [] # 可信度列表
ci_width_list = [] # 置信区间宽度列表
ci_upper_limit = [] # 置信区间上极限
ci_lower_limit = [] # 置信区间下极限
for i in range(20): 
    print("alpha={}".format(alpha))
    # 均值的99%可信区间的置信区间
    """  置信区间  """
    df = len(data.rate) - 1
    ci = stats.t.interval(alpha, df, loc=np.mean(data.rate), scale=stats.sem(data.rate))
    # ci = stats.t.interval(alpha=0.99,df=len(data.rate)-1,loc=np.mean(data.rate),scale=stats.sem(data.rate))

    # 算出置信区间的宽度
    ci_element = ci

    ci_lower_limit.append(ci_element[0])
    ci_upper_limit.append(ci_element[1])
    # ci_element.append(ci)
    ci_width = ci_element[1] - ci_element[0] # 定义置信区间宽度
    ci_width_list.append(ci_width)
    print(ci_width)  # 输出置信区间宽度

    alpha_list.append(alpha) # 添加到列表中
    alpha = alpha - 0.05
    print("置信区间={}".format(ci))
    print("  "*100)

print(ci_width_list)
print(alpha_list)
x=alpha_list # 设置可信度为x轴
# y=ci_width_list

plt.plot(x,ci_lower_limit,linestyle="dashdot",label="置信区间下极限")
plt.plot(x,ci_width_list,linestyle="dashdot",label = "置信区间宽度")
plt.plot(x,ci_upper_limit,linestyle="dashdot",label= "置信区间上极限")
plt.xlabel("可信度/百分数") # 可信度指的是可信区间, 为了方面理解,用可信度代替可信区间
plt.ylabel("置信区间/单位为变量的单位")
plt.title("可信度--置信区间宽度 图")
plt.legend() # 显示标签
"""
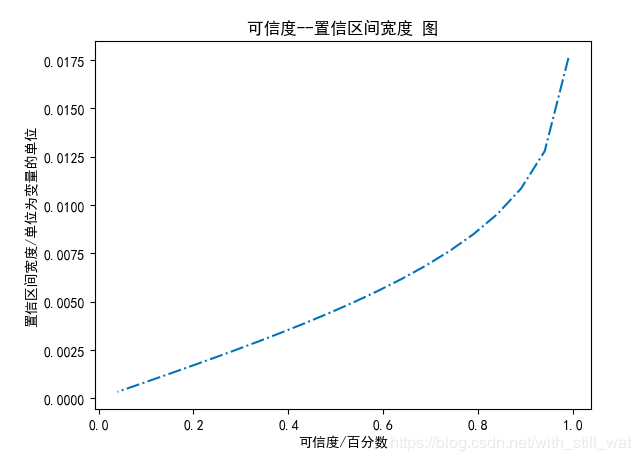
可信度与置信区间图说明:
例如:可信度=0.90,置信区间宽度=0.05, 置信区间上限=0.07,置信区间下限=0.02
则说明:发生在区间(0.02,0.07)这个范围内的可能性为0.90

通过图像得出: 置信区间宽度越越小,预测模型越精确;但是置信区间宽度小了,可信度也就越小了
"""
plt.show()

　　

 

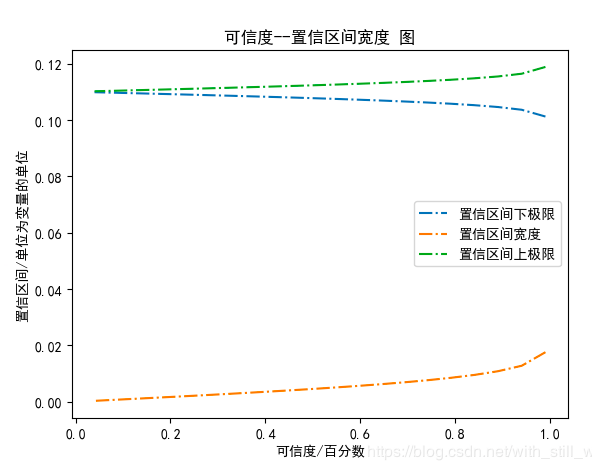
通过图可以得出上述结论:
:置信区间宽度越小,预测模型越精确;但是置信区间宽度小了,可信度也就越小了

所有为了得到较高的可信度, 就必须得扩大置信区间宽度; 一般取可信度=0.95来计算

原文：https://blog.csdn.net/with_still_water/article/details/102511633