SDNU_ACM_ICPC_2021_Winter_Practice_5th [个人赛]

传送门

I - Stone

题意：

唐和江进行游戏，规则是，对于给定的n和k，唐先手，在黑板上写出[1，k]的数，再加下来每次写的数必须>=上次的数加1，<=上次的数加k，谁写出的先超过n即输

思路：

巴什博弈的变形。巴什博弈是n到0输，现在是1到n输，我们可以把它看成n - 1到0的巴什博弈即可，当（n - 1）% k == 0时先手输，即江赢，否则唐赢

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int main()
{
    int n, m;
    while(cin>>n>>m)
    {
        if(n == 0 && m == 0)
            break;
        else
        {
            if((n - 1) % (m + 1) == 0)
                cout<<"Jiang
";
            else
                cout<<"Tang
";
        }
    }
    return 0;
}

A - Strange Partition

题意：

给你n个数和x，问你这个n个数可以进行无数次两两相加，问你经过操作后数组的数对k向上取整的最小值和最大值为多少

思路：

对于任意一个数k，我们可以把它拆成两部分看：(k / x ) * x + k % 4，也就是x的倍数加上对x的余数，由于是向上取整，所以余数无论是多少都无所谓（0除外）,都会进1的，所以最小值只需要我们让每个数的余数尽量为0即可，所以可以把所有的值加起来，对x向上取整即可。

而对于最大值，就是每个数对x向上取整，然后加起来即可。

因为我忘了向上取整的函数是多少，所以我就用（k + x - 1）/ x 来代替函数，其结果是一样的

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int IntRead()
{
    char ch = getchar();
    int s = 0, w = 1;
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
            w = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        s = s * 10 + ch - '0',
        ch = getchar();
    }
    return s * w;
}
int main()
{
    ll t, n, x;
    ll tr[100005];
    t = IntRead();
    while(t--)
    {
        memset(tr, 0, sizeof(tr));
        ll ans = 0, sum = 0, k = 0;
        n = IntRead();
        x = IntRead();
        for(int i = 1; i <= n; i++)
        {
            tr[i] = IntRead();
            sum += tr[i];//求和
            ans += (tr[i] + x - 1) / x;//对每个数进行向上取整
        }
        ll minx = (sum + x - 1) / x;//对和进行向上取整
        ll maxn = ans;
        cout<<minx<<' '<<maxn<<'
';
    }
    return 0;
}

H - Red and Blue

题意：

给出n+m个数，n个数与m个数是两列数，但他们本来是一列数，问你这列数如何摆放能放下面的f(a)的值最大（这两列数内的数相对顺序不变）

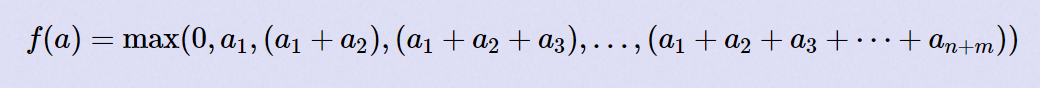
思路：

想一下就可以知道这个题考察的是前缀和，只需对两堆数求前缀和即可，但记得求完前缀和与0比大小（我就这样不小心wa了一发，逃

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
inline int IntRead()
{
    char ch = getchar();
    int s = 0, w = 1;
    while(ch < '0' || ch > '9')
    {
        if(ch == '-')
            w = -1;
        ch = getchar();
    }
    while(ch >= '0' && ch <= '9')
    {
        s = s * 10 + ch - '0',
        ch = getchar();
    }
    return s * w;
}
int main()
{
    ll t, n, m, ar[105],br[105],arr[105], brr[105];
    t = IntRead();
    while(t--)
    {
        ll max1 = -1e9, max2 = -1e9;
        memset(arr, 0, sizeof(arr));//初始化
        memset(brr, 0, sizeof(brr));
        memset(ar, 0, sizeof(ar));
        memset(br, 0, sizeof(br));
        n = IntRead();
        for(int i = 1; i <= n; i++)
        {
            ar[i] = IntRead();
        }
        for(int i = 1; i <= n; i++)
        {
            arr[i] = arr[i - 1] + ar[i];
            max1 = max(max1, arr[i]);//找最大前缀和
        }
        m = IntRead();
        for(int i = 1; i <= m; i++)
        {
            br[i] = IntRead();
        }
        for(int i = 1; i <= m; i++)
        {
            brr[i] = brr[i - 1] + br[i];
            max2 = max(max2, brr[i]);//同样是找最大前缀和
        }
        max1 = max(0, max1);
        max2 = max(0, max2);
        if(max1 <= 0 && max2 >= 0)
            cout<<max2<<'
';
        else if(max1 <= 0 && max2 <= 0)
            cout<<0<<'
';
        else if(max1 >= 0 && max2 >= 0)
            cout<<max1 + max2<<'
';
        else if(max1 >= 0 && max2 <= 0)
            cout<<max1<<'
';
if(max1 <= 0 && max2 >= 0)
            cout<<max2<<'
';
        else if(max1 <= 0 && max2 <= 0)
            cout<<0<<'
';
        else if(max1 >= 0 && max2 >= 0)
            cout<<max1 + max2<<'
';
        else if(max1 >= 0 && max2 <= 0)
            cout<<max1<<'
';
        cout<<max1 + max2<<'
';
    }
    return 0;
}

B - Strange List

题意：

给你一个n个数，和一个数x，从第一个数开始进行判断，如果能除得尽就将整除后得到的数按整除的份数放到这堆数的后面，一直这样下去，最终求得这堆数的和

举个栗子：

1 2 ##1是这个堆数本来的数量，2是除数

12 ##12 是那对数

12 6 6 3 3 3 3 ##12除2得道两个6，所以放在那对数里面，6除以2得到两个3，6除以2得到两个3,3除不尽2，所以停止下来

思路：

我当时想用数组来做，但是怕爆了，所以想换queue，发现不能用迭代器，还怕TLE，就另辟蹊径：因为每次都是把除完的数全放到后面，所以一个数除完放在后面，他们的和是不变的，即12 -> 12 6 6 3 3 3 3, 6+6 = 12， 3 + 3 = 6 。相当于12 * 3。所以就不必循环跑，只要知道算了几次和即可，也就是要确定是哪里先出现奇数，只需要单独写个函数，对每个数求需要除几次2能变成奇数即可，靠前的最小数即是我们要找的

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll tr[100005], ar[100005];
ll t, n, x, k, sum = 0;
ll f(ll y)//这是函数f（），用来求除几次2能得到奇数的
{
    ll len = 0;
    while(1)
    {
        if(y % x == 0)
        {
            y /= x;
            len++;
        }
        else
            break;
    }
    return len;
}
int main()
{
    cin>>t;
    while(t--)
    {
        memset(tr, 0, sizeof(tr));//因为是多组输入，所以千万不要忘记清0数组
        memset(ar, 0, sizeof(ar));
        sum = 0;
        ll step = 1, minx = 1e9;
        cin>>n>>x;
        for(int i = 1; i <= n; i++)
        {
            cin>>tr[i];
            sum += tr[i];//记录一次的总和
            ar[i] = f(tr[i]);
            if(ar[i] < minx)//比较，找到位置
            {
                step = i;//记录位置
                minx = ar[i];//更新最小值
            }
        }
        ll ans = (f(tr[step]) + 1) * sum;//+1是因为要算上刚开始的数的和
        for(int i = 1; i <= step - 1; i++)
        {
            ans += tr[i];//因为上面求的step不一定是第一个数，所以肯定会加上其他的，你写个例子就懂了，这里不赘述
        }
        cout<<ans<<endl;
    }
    return 0;
}

K - Period

题意：

给你一个字符串，让你求其前缀串是否是循环串，如果是就输出位置和循环次数

思路：

上次刚做了一个问字符串是不是循环子串的题，这个题就是她的变式，只不过这次需要循环求其前缀串，上次只需要求这个字符串，思路都是求i - next[i],看看字符串的长度能否除尽这个数即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll next1[1000005], len1;
string s;
void getnext1()//第一个字符串的next数组的构造
{
    int j, k;
    j = 0;
    k = -1;
    next1[0] = -1;
    while(j < len1)
    {
        if(k == -1 || s[j] == s[k])
            next1[++j] = ++k;
        else
            k = next1[k];
    }
}
int main()
{

    int t, q = 1;
    while(cin>>len1 && len1)
    {
        cout<<"Test case #"<<q<<endl;
        q++;
        cin>>s;
        memset(next1, 0, sizeof(next1));
        getnext1();
        for(int i = 1; i < len1; i++)//因为题中说从第二个字符开始，所以相当于字符串的1的索引
        {//因为输出的是字符的位置，不是从0开始的，所以要稍加改变
            int a = i + 1 - next1[i + 1];
            if((i + 1) % a == 0 && (i + 1) / a != 1)
                cout<<i + 1<<' '<<(i + 1) / a<<endl;
        }
        cout<<endl;
    }
    return 0;
}

G - Common Subsequence

题意：

求两个字符串最大公共子序列

思路：

dp

当s[i] == ss[j]，那么对于s[i]和ss[j]的最大公共子序列就相当于是s[i - 1]与ss[j - 1]的最大公共子序列。

当s[i] != ss[j]，那么对于s[0 ……i] 和 ss[0 ……j]的最大公共子序列的值是s[0 …… i-1]与ss[0……j]的最大公共子序列的长度 或 s[0 …… i]与ss[0 …… j - 1]的最大公共子序列的长度，因为是最大，所以取最大值即可

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[1005][1005];
string s, ss;
int main()
{
    while(cin>>s>>ss)
    {
        memset(dp, 0, sizeof(dp));
        int n = s.size();
        int m = ss.size();
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= m; j++)
            {
                if(s[i - 1] == ss[j - 1])
                    dp[i][j] = dp[i - 1][j - 1] + 1;
                else
                    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
        cout<<dp[n][m]<<'
';
    }
    return 0;
}

C - Strange Birthday Party

题意：

n个朋友，m个礼物，礼物是c[]，朋友的序号是tr[]

对于每个朋友，送的东西有两种选择，一是从第一个到第tr[i]个礼物里面挑一个，二是直接送第c[i]块钱，切记，每个礼物只有一个，让你花最少的钱解决所有人的东西。

思路：

贪心。因为礼物的价值的升序排列，所有可以对朋友的序号排序，序号大的人选择多，但直接塞钱贵，序号小的选择少，但塞钱便宜啊，所以我们可以从序号大的开始循环，礼物从小的开始给，给完就换下一个，当礼物送完或者，剩下的礼物贵于直接塞钱，那就塞钱！

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll t, sum, k, n, m, tr[300005],c[300005];
inline int IntRead(){
    char ch = getchar();
    int s = 0, w = 1;
    while(ch < '0' || ch > '9'){
        if(ch == '-')
            w = -1;
        ch = getchar();}
    while(ch >= '0' && ch <= '9'){
        s = s * 10 + ch - '0',
        ch = getchar();}
    return s * w;
}

int main()
{
    t = IntRead();
    while(t--)
    {
        n = IntRead();
        m = IntRead();
        for(int i = 1; i <= n; i++)
            tr[i] = IntRead();
        for(int i = 1; i <= m; i++)
            c[i] = IntRead();
        sort(tr + 1, tr + 1 + n);
        k = 1;
        sum = 0;
        for(int i = n; i > 0; i--)
        {
            if(tr[i] > k)
                sum += c[k++];
            else
                sum += c[tr[i]];
        }
        cout<<sum<<endl;
    }
    return 0;
}

总结

I题妥妥的巴什博弈，我前一天还刚看过这个题，结果当时没仔细看题，草草了事，导致今日做题明明知道做法却因为0%x=0都不知道，样例死都算不对，就不敢写，后来写出来运行后发现0%x=0，人都傻了

B题一个简单的思维题，开始想复杂了，后来发现没必要那样算，只需要算一下所有的和以及对每个数向上取整的和即可

H题一个前缀和题，求两列数的前缀和的值的和的最大值即可，记得求完前缀和不要直接相加，要看看是不是小于0！

B题也是思维题，算一下是哪个数最靠前且除2出现次数最小，然后将最后的和分为两部分算即可

K题循环子串的问题

C题贪心

G题dp求最大相同子序列