矩阵的行列计算

题目网址：http://codeforces.com/problemset/problem/405/C

C. Unusual Product

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Little Chris is a huge fan of linear algebra. This time he has been given a homework about the unusual square of a square matrix.

The dot product of two integer number vectors x and y of size n is the sum of the products of the corresponding components of the vectors. The unusual square of an n × n square matrix A is defined as the sum of n dot products. The i-th of them is the dot product of the i-th row vector and the i-th column vector in the matrix A.

Fortunately for Chris, he has to work only in GF(2)! This means that all operations (addition, multiplication) are calculated modulo 2. In fact, the matrix A is binary: each element of A is either 0 or 1. For example, consider the following matrix A:

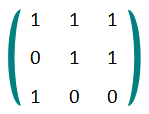
The unusual square of A is equal to (1·1 + 1·0 + 1·1) + (0·1 + 1·1 + 1·0) + (1·1 + 0·1 + 0·0) = 0 + 1 + 1 = 0.

However, there is much more to the homework. Chris has to process q queries; each query can be one of the following:

1. given a row index i, flip all the values in the i-th row in A;
2. given a column index i, flip all the values in the i-th column in A;
3. find the unusual square of A.

To flip a bit value w means to change it to 1 - w, i.e., 1 changes to 0 and 0 changes to 1.

Given the initial matrix A, output the answers for each query of the third type! Can you solve Chris's homework?

Input

The first line of input contains an integer n (1 ≤ n ≤ 1000), the number of rows and the number of columns in the matrix A. The next nlines describe the matrix: the i-th line contains n space-separated bits and describes the i-th row of A. The j-th number of the i-th lineaij (0 ≤ aij ≤ 1) is the element on the intersection of the i-th row and the j-th column of A.

The next line of input contains an integer q (1 ≤ q ≤ 106), the number of queries. Each of the next q lines describes a single query, which can be one of the following:

• 1 i — flip the values of the i-th row;
• 2 i — flip the values of the i-th column;
• 3 — output the unusual square of A.

Note: since the size of the input and output could be very large, don't use slow output techniques in your language. For example, do not use input and output streams (cin, cout) in C++.

Output

Let the number of the 3rd type queries in the input be m. Output a single string s of length m, where the i-th symbol of s is the value of the unusual square of A for the i-th query of the 3rd type as it appears in the input.

Sample test(s)

input

3
1 1 1
0 1 1
1 0 0
12
3
2 3
3
2 2
2 2
1 3
3
3
1 2
2 1
1 1
3

output

01001

思路：易知求A时若i！=j 则a[i][j]*a[j][i]会使用两次，对2求余时没有影响，若i==j a[i][j]*a[j][i]即a[i][i]*a[i][i]算一次，所以A等于对角线（i==j）上所有元素之和对2求余。而每次行或列变化 对角线上只有一个元素变化，所以行或列变化一次A变化一次（1->0或0->1)。

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <cmath>
using namespace std;
int a[1005][1005];
int c[1000005];

int main()
{
    int n,q;
    int i,j,x,num;
    while(scanf("%d",&n)!=EOF)
    {
        num=0;
        for(i=1;i<=n;i++)
        for(j=1;j<=n;j++)
        scanf("%d",&a[i][j]);
        scanf("%d",&q);
        int sum=0;
        for(i=1;i<=n;i++)
        sum+=a[i][i];
        sum=sum%2;
        while(q--)
        {
            scanf("%d",&x);
            if(x==3)
            c[num++]=sum;
            else
            {
                scanf("%d",&x);
                sum=(sum+1)%2;
            }
        }
        for(i=0;i<num;i++)
        printf("%d",c[i]);
        printf("
");
    }
    return 0;
}