题目链接
问题描述

输入描述
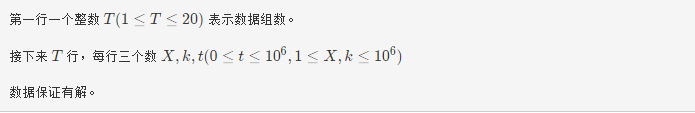
输出描述

输入样例

输出样例

题意:中文题,不再赘述;
思路: BC题解如下:
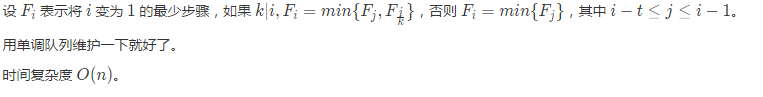
从后往前推,可以得到状态转移方程dp[i]=(dp[k*i],dp[i+l])+1{1<=l<=t}
根据这个转移方程我们需要快速求得min{dp[i+l]}(1<=l<=t)
我们知道这种形式的就是单调队列优化dp的标准形式
维护一个dp[i]从队头到队尾递增的队列 每次算好dp[i]的时候把队尾中dp值大于等于dp[i]的都出队 (出队都是下标比i大的,值又没i优,是无用的)
然后dp[i]=min(dp[a[pre]],dp[k*i])+1
代码如下:
#include <iostream> #include <algorithm> #include <stdio.h> #include <cstring> #include <cmath> #include <queue> #include <set> #include <bitset> using namespace std; typedef long long LL; int dp[1000005],a[1000005]; int pre,tail; int main() { int T,x,k,t; cin>>T; while(T--) { scanf("%d%d%d",&x,&k,&t); pre=0,tail=0; a[tail++]=x; dp[x]=0; for(int i=x-1;i>=1;i--) { dp[i] = (t!=0)?dp[a[pre]]+1:9999999; if((1LL*i*k)<=(LL)x) dp[i]=min(dp[i],dp[i*k]+1); if(a[pre]-t==i) pre++; while(dp[a[tail-1]]>=dp[i]&&tail>pre) tail--; a[tail++]=i; } printf("%d ",dp[1]); } return 0; }