Problem Description
Once upon a time Matt went to a small town. The town was so small and narrow that he can regard the town as a pivot. There were some skyscrapers in the town, each located at position xi with its height hi. All skyscrapers located in different place. The skyscrapers had no width, to make it simple. As the skyscrapers were so high, Matt could hardly see the sky.Given the position Matt was at, he wanted to know how large the angle range was where he could see the sky. Assume that Matt's height is 0. It's guaranteed that for each query, there is at least one building on both Matt's left and right, and no building locate at his position.
Input
The first line of the input contains an integer T, denoting the number of testcases. Then T test cases follow.
Each test case begins with a number N(1<=N<=10^5), the number of buildings.
In the following N lines, each line contains two numbers, xi(1<=xi<=10^7) and hi(1<=hi<=10^7).
After that, there's a number Q(1<=Q<=10^5) for the number of queries.
In the following Q lines, each line contains one number qi, which is the position Matt was at.
Each test case begins with a number N(1<=N<=10^5), the number of buildings.
In the following N lines, each line contains two numbers, xi(1<=xi<=10^7) and hi(1<=hi<=10^7).
After that, there's a number Q(1<=Q<=10^5) for the number of queries.
In the following Q lines, each line contains one number qi, which is the position Matt was at.
Output
For each test case, first output one line "Case #x:", where x is the case number (starting from 1).
Then for each query, you should output the angle range Matt could see the sky in degrees. The relative error of the answer should be no more than 10^(-4).
Then for each query, you should output the angle range Matt could see the sky in degrees. The relative error of the answer should be no more than 10^(-4).
Sample Input
3
3
1 2
2 1
5 1
1
4
3
1 3
2 2
5 1
1
4
3
1 4
2 3
5 1
1
4
Sample Output
Case #1:
101.3099324740
Case #2:
90.0000000000
Case #3:
78.6900675260
题意:有n栋楼房在一条直线上,其宽度忽略不计,它们所在位置和楼房高度用(xi,yi)表示,现在有Q次询问,每次输入一个人的位置 x ,求这个人的视角范围,可以保证所有的楼房和人的位置都不会相同(不会在同一点出现两个楼房或者楼房和人)。
思路:
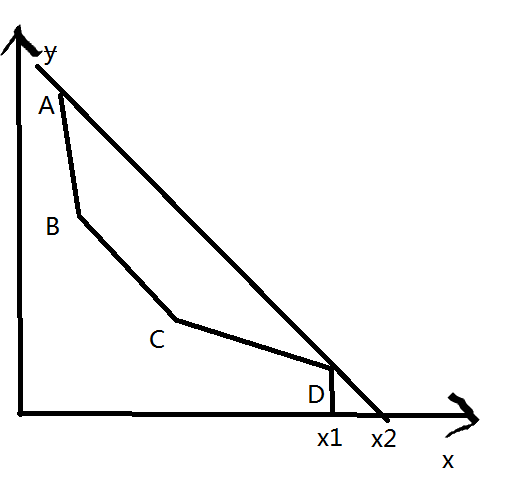
对于上图的情况,可以发现B和C点没有用,对以后的观察视角不会产生影响,为什么呢?从x1到x2之间D点影响视角,而x2后则是A点影响视角。
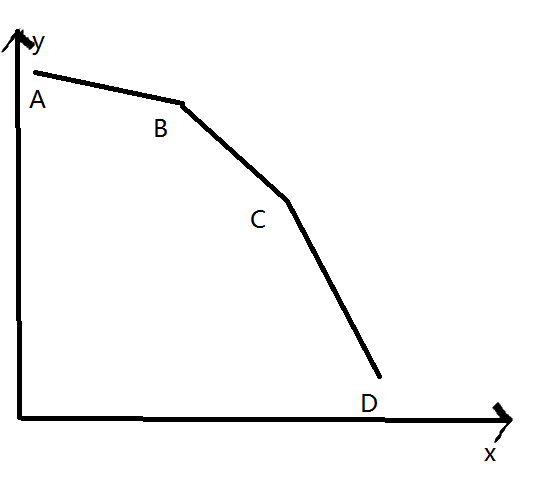
由上图可以发现ABCD四点都有影响,当距离D点较近时D点对视角产生影响,但继续向右走时C开始影响视角,再向右走时就是B产生影响,接着是A。
由上面两幅图可以发现:只有斜率的绝对值越来越大时,才有可能这些点都对视角产生影响,如果不满足斜率增大则将前一个点去掉,直到满足斜率的绝对值递增,这样可以用单调栈来维护。
代码如下:
#include <iostream> #include <algorithm> #include <cstdio> #include <cstring> #include <cmath> using namespace std; const int maxn=1e5+5; const double PI=acos(-1); struct Node{ double x; double y; int L,R,id; }a[2*maxn]; int top,s[maxn]; bool cmp(const Node s1,const Node s2) { return s1.x<s2.x; } bool cmp2(const Node s1,const Node s2) { return s1.id<s2.id; } double cal2(double x,double y) { //cout<<"H:"<<x<<" "<<y<<endl; return atan(y/x); } int main() { ///cout << "Hello world!" << endl; int T,Case=1; cin>>T; while(T--) { printf("Case #%d: ",Case++); int N; scanf("%d",&N); for(int i=1;i<=N;i++) scanf("%lf%lf",&a[i].x,&a[i].y),a[i].id=i; int Q; scanf("%d",&Q); for(int i=N+1;i<=N+Q;i++) scanf("%lf",&a[i].x),a[i].y=0,a[i].id=i; sort(a+1,a+N+Q+1,cmp); ///for(int i=1;i<=N+Q;i++) cout<<a[i].id<<" "<<a[i].x<<" "<<a[i].y<<endl; top=0; s[0]=1; for(int i=2;i<=N+Q;i++) { while(1) { if(top<1) break; double x1=a[s[top]].x-a[s[top-1]].x; double y1=a[s[top]].y-a[s[top-1]].y; //double f1=cal(a[s[top-1]].x, a[s[top-1]].y, a[s[top]].x, a[s[top]].y); double x2=a[i].x-a[s[top]].x; double y2=a[i].y-a[s[top]].y; //double f2=cal(a[s[top]].x, a[s[top]].y, a[i].x, a[i].y); if(y1*x2>y2*x1) break; top--; } if(a[i].id>N) a[i].L=a[s[top]].id;//,cout<<"top1 "<<top<<" "<<s[top]<<" "<<a[s[top]].id<<endl; s[++top]=i; } top=0; s[0]=N+Q; for(int i=N+Q-1;i>=1;i--) { while(1) { if(top<1) break; double x1=a[s[top-1]].x-a[s[top]].x; double y1=a[s[top-1]].y-a[s[top]].y; //double f1=cal(a[s[top-1]].x, a[s[top-1]].y, a[s[top]].x, a[s[top]].y); double x2=a[s[top]].x-a[i].x; double y2=a[s[top]].y-a[i].y; //double f2=cal(a[s[top]].x, a[s[top]].y, a[i].x, a[i].y); if(y1*x2<y2*x1) break; top--; } if(a[i].id>N) a[i].R=a[s[top]].id;//,cout<<"top2 "<<top<<" "<<s[top]<<" "<<a[s[top]].id<<endl; s[++top]=i; } sort(a+1,a+N+Q+1,cmp2); for(int i=N+1;i<=N+Q;i++) { //cout<<"--->"<<a[i].L<<" "<<a[i].R<<endl; double ans=PI; int k=a[i].L; ans-=cal2(a[i].x-a[k].x,a[k].y); k=a[i].R; ans-=cal2(a[k].x-a[i].x,a[k].y); printf("%.10f ",ans*180/PI); } } return 0; }