day10

目录

• 梯度下降算法
  • 梯度下降法的概念图（二维）：
  • 找到最优解的三个步骤
  • 梯度下降法具体实现(一维)
• 计算图
  • 概念
  • 简单说明
• Logistic 回归的梯度下降法

梯度下降算法

• 梯度下降法是一种致力于找到函数极值点的算法
• 通过大量训练步骤将损失（也就是成本函数 J(w,b) ）最小化,从而训练参数w，b

梯度下降法的概念图（二维）：

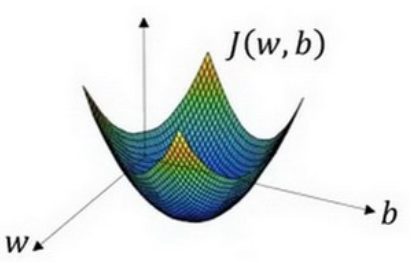
在这里w和b都是实数（在实践中w可以是更高的维度），我们要做的其实就是使得成本函数达到极小值，求得对应的w和b。

注：前面我们设计成本函数 J(w,b) 时，特意的使得它是一个凸函数,为的就是唯一的极值而不是多个局部最优解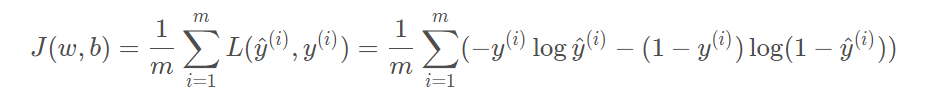

虽然多个局部最优解可以通过随机初始化的方法解决，但在逻辑回归中我们还是选择凸函数。

找到最优解的三个步骤

1. 初始化
2. 朝最陡的下坡方向走一步，不断地迭代
3. 直到走到全局最优解或者接近全局最优解的地方

梯度下降法具体实现(一维)

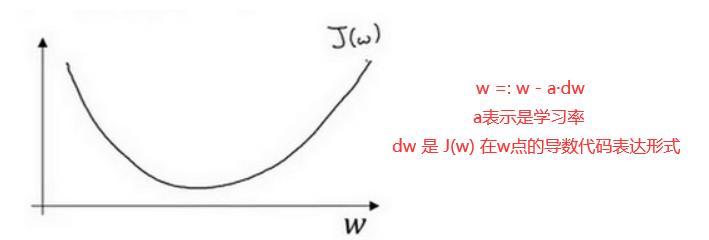
我们前面的三个步骤中

• 朝最陡的下坡方向也就是沿着曲线某点的斜率（导数）
• 不断迭代也就是重复做图片红字公式（牛顿下山法），不断更新w，从而使得 J(w) 取得最小
• α 表示学习率（learning rate），用来控制步长（step）

同理对于二维的，也就是两个参数的 J(w,b) ，导数就变成了偏导

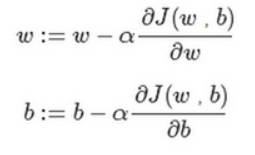
计算图

概念

​ 一个机器学习任务的核心是模型的定义以及模型的参数求解方式，对这两者进行抽象之后，可以确定一个 唯一的计算逻辑，将这个逻辑用图表示，称之为计算图。计算图表现为有向无环图，定义了数据的流转方式， 数据的计算方式，以及各种计算之间的相互依赖关系等。

简单说明

​ 可以说，一个神经网络的计算，都是按照前向或反向传播过程组织的。首先我们计算出一个新的网络的输出 (前向过程)，紧接着进行一个反向传播操作。后者我们用来计算出对应的梯度或导数，也就是链式求导。

​

​ 蓝线：前向传播；红线：反向传播。计算图对于我们后面求dw时有帮助。

Logistic 回归的梯度下降法

回顾之前的一些公式，并做简单说明。

​

注：1*n的矩阵和n*1的矩阵相乘得到的就是一个数，1*1的矩阵可以当成常数

然后就可以反向传播，利用链式求导求得想要的导数。