Python 手写数字识别-knn算法应用

　　在上一篇博文中，我们对KNN算法思想及流程有了初步的了解，KNN是采用测量不同特征值之间的距离方法进行分类，也就是说对于每个样本数据，需要和训练集中的所有数据进行欧氏距离计算。这里简述KNN算法的特点：

优点：精度高，对异常值不敏感，无数据输入假定
缺点：计算复杂度高，空间复杂度高
适用数据范围：数值型和标称型（具有有穷多个不同值,值之间无序）

　   knn算法代码：

#-*- coding: utf-8 -*-
from numpy import *
import operator
import time
from os import listdir

def classify(inputPoint,dataSet,labels,k):
    dataSetSize = dataSet.shape[0]     #已知分类的数据集（训练集）的行数
    #先tile函数将输入点拓展成与训练集相同维数的矩阵，再计算欧氏距离
    diffMat = tile(inputPoint,(dataSetSize,1))-dataSet  #样本与训练集的差值矩阵
    sqDiffMat = diffMat ** 2                    #差值矩阵平方
    sqDistances = sqDiffMat.sum(axis=1)         #计算每一行上元素的和
    distances = sqDistances ** 0.5              #开方得到欧拉距离矩阵
    sortedDistIndicies = distances.argsort()    #按distances中元素进行升序排序后得到的对应下标的列表
    #选择距离最小的k个点
    classCount = {}
    for i in range(k):
        voteIlabel = labels[ sortedDistIndicies[i] ]
        classCount[voteIlabel] = classCount.get(voteIlabel,0)+1
    #按classCount字典的第2个元素（即类别出现的次数）从大到小排序
    sortedClassCount = sorted(classCount.items(), key = operator.itemgetter(1), reverse = True)
    return sortedClassCount[0][0]

　　下面介绍如何使用knn算法对手写识别数据进行分类，这里构造的分类系统只能识别数字0到9，数字经图形处理软件处理成具有相同的色彩和大小，宽高为32x32像素，为了便于处理，已将图像转换为文本格式，其效果图如下：

　　数据集可在这里下载，解压后有两个目录，其中目录trainingDigits中包含了1934个例子，命名规则如 9_45.txt，表示该文件的分类是9，是数字9的第45个实例，每个数字大概有200个实例。testDigits目录中包含946个例子。使用trainingDigits中的数据作为训练集，使用testDigits中的数据作为测试集测试分类的效果。两组数据没有重叠。

　　算法应用步骤如下：

　　1. 数据准备：数字图像文本向量化，这里将32x32的二进制图像文本矩阵转换成1x1024的向量。循环读出文件的前32行，存储在向量中。

#文本向量化 32x32 -> 1x1024
def img2vector(filename):
    returnVect = []
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect.append(int(lineStr[j]))
    return returnVect

　　2. 构建训练数据集：利用目录trainingDigits中的文本数据构建训练集向量，以及对应的分类向量

#从文件名中解析分类数字
def classnumCut(fileName): 
　  fileStr = fileName.split('.')[0]  
    classNumStr = int(fileStr.split('_')[0]) 
    return classNumStr
#构建训练集数据向量，及对应分类标签向量
def trainingDataSet():
    hwLabels = []
    trainingFileList = listdir('trainingDigits')           #获取目录内容
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))                          #m维向量的训练集
    for i in range(m):
        fileNameStr = trainingFileList[i]
        hwLabels.append(classnumCut(fileNameStr))
        trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
    return hwLabels,trainingMat

　　3. 测试集数据测试：通过测试testDigits目录下的样本，来计算算法的准确率。

#测试函数
def handwritingTest():
    hwLabels,trainingMat = trainingDataSet()    #构建训练集
    testFileList = listdir('testDigits')        #获取测试集
    errorCount = 0.0                            #错误数
    mTest = len(testFileList)                   #测试集总样本数
    t1 = time.time()
    for i in range(mTest):
        fileNameStr = testFileList[i]
        classNumStr = classnumCut(fileNameStr)
        vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
　　　　 #调用knn算法进行测试
        classifierResult = classify(vectorUnderTest, trainingMat, hwLabels, 3)
        print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)
        if (classifierResult != classNumStr): errorCount += 1.0
    print "
the total number of tests is: %d" % mTest               #输出测试总样本数
    print "the total number of errors is: %d" % errorCount           #输出测试错误样本数
    print "the total error rate is: %f" % (errorCount/float(mTest))  #输出错误率
    t2 = time.time()
    print "Cost time: %.2fmin, %.4fs."%((t2-t1)//60,(t2-t1)%60)      #测试耗时

if __name__ == "__main__":
    handwritingTest()

　　运行结果如下：

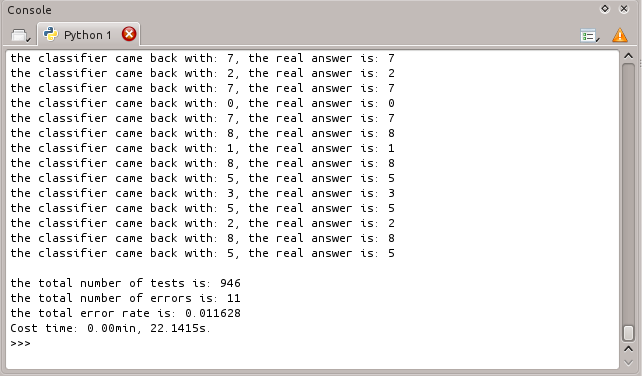
　　利用knn算法识别手写数字数据集，错误率为1.6%，算法的准确率还算可观。也可以通过改变变量k的值，观察错误率的变化，关于k值的选择，一般取一个比较小的数值，例如采用交叉验证法（简单来说，就是一部分样本做训练集，一部分做测试集）来选择最优的K值。

　　通过运行以上代码，我们会发现knn算法的执行效率并不高，因为算法需要为每个测试向量计算约2000次欧氏距离，每个距离计算包括1024个维度浮点运算，全部样本要执行900多次，可见算法实际耗时长，另外，knn算法必须保存全部数据集，每次需为测试向量准备2MB的存储空间（2个1024x1024矩阵的空间）。所以如何优化算法，减少存储空间和计算时间的开销，需要我们进一步深入学习。

参考资料：

　　《机器学习实战》