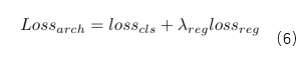DMCP
2020-CVPR-DMCP Differentiable Markov Channel Pruning for Neural Networks
来源:ChenBong 博客园
- Shaopeng Guo(sensetime 商汤)
- GitHub: 64 stars
- https://github.com/zx55/dmcp
Introduction
propose a novel differentiable channel pruning method named Differentiable Markov Channel Pruning (DMCP) to perform efficient optimal sub-structure searching.
本文提出DMCP(可微分的通道剪枝)来高效地搜索子空间。
At the same FLOPs, our method outperforms all the other pruning methods both on MobileNetV2 and ResNet, as shown in Figure 1.
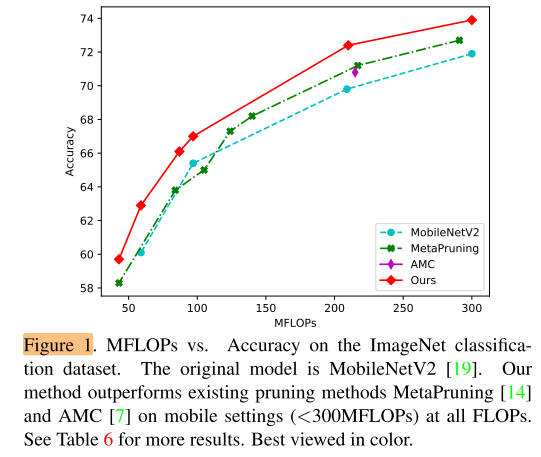
With our method, MobileNetV2 has 0.1% accuracy drop with 30% FLOPs reduction and the FLOPs of ResNet-50 is reduced by 44% with only 0.4% drop.
Motivation
Recent works imply that the channel pruning can be regarded as searching optimal sub-structure from unpruned networks.
通道的修剪可以视为从未修剪的网络中搜索最佳的子结构(网络剪枝得到的子结构比继承的权重更重要)
However, existing works based on this observation require training and evaluating a large number of structures, which limits their application.
之前的工作需要训练和评估很多子结构,开销大
Conventional channel pruning methods mainly rely on the human-designed paradigm.
卷积网络的剪枝主要依靠手工设计的范式(重要性指标)
the structure of the pruned model is the key of determining the performance of a pruned model, rather than the inherited “important” weights.
剪枝后网络的结构对性能的影响更大,而不是所继承的”重要“权重
the optimization of these pruning process need to train and evaluate a large number of structures sampled from the unpruned network, thus the scalability of these methods is limited.
之前的(搜索子结构)的剪枝方法需要训练和评估大量的网络,因此可扩展性(修剪不同大小的网络)受到限制
A similar problem in neural architecture search (NAS) has been tackled by differentiable method DARTS
在NAS中也有类似的问题,已经被可微分方法DARTS解决了
ps 与DATRS的区别
First, the definition of search space is different. The search space of DARTS is a category of pre-defined operations (convolution, max-pooing, etc), while in the channel pruning, the search space is the number of channels in each layer.
第一,搜索空间的不同。DARTS的搜索空间是一些预定义的操作,而我们的搜索空间是不同层通道的数量
Second, the operations in DARTS are independent with each other. But in the channel pruning, if a layer has k + 1 channels, it must have at least k channels first, which has a logical implication relationship.
第二,DARTS中的操作时互相独立的(比如两个node的连接之间的不同操作,卷积,池化,互不影响),但通道剪枝中,如果一层有k+1个通道,那么它首先要有k个通道。
Contribution
Our method makes the channel pruning differentiable by modeling it as a Markov process.
我们通过将模型剪枝建模为马尔科夫过程,从而使之可以微分
Method
Our method is differentiable and can be directly optimized by gradient descent with respect to standard task loss and budget regularization (e.g. FLOPs constraint).
DMCP中,我们将通道剪枝视为markov(马尔科夫)过程,剪枝中的markov状态(state)代表是否保留相应的通道,状态之间的转移视为剪枝的过程
In the Markov process for each layer, the state (S_k) represents the (k^{th}) channel is retained, the transition from (S_k) to (S_{k+1}) represents the probability of retaining the (k+1)th channel given that the kth channel is retained.
每一层为一个马尔科夫过程,状态 (S_k) 表示保留第k个通道。状态 (S_k) 到 (S_{k+1}) 的转移代表保留第k+1个通道的概率
Note that the start state is always (S_1) in our method.
(S_1) 是起始状态,即每层都至少有1个通道
Then the marginal probability for state (S_k), i.e. the probability of retaining (k^{th}) channel, can be computed by the product of transition probabilities and can also be viewed as a scaling coefficient.
因此,第k个状态(保留第k个通道)的边缘概率=之前所有转移概率的乘积,可以视为第k个通道的放大系数
Each scaling coefficient is multiplied to its corresponding channel’s feature map during the network forwarding.
前向过程中,每个通道的feature map 乘以 该通道对应的 边缘概率(放大系数)
So the transition probabilities parameterized by learnable parameters can be optimized in an end-to-end manner by gradient descent with respect to task loss together with budget regularization (e.g. FLOPs constraint).
因此可以通过对目标loss 和 代价loss(FLOPs loss)的梯度下降,来end to end地优化 不同层,不同通道的转移概率
After the optimization, the model within desired budgets can be sampled by the Markov process with learned transition probabilities and will be trained from scratch to achieve high performance.
优化完成后(即网络中每一层的转移概率/边缘概率 可以抽样出符合FLOPs限制的网络了),进行采样子网络并从头开始训练
因此,DMCP选择将剪枝的过程建模为一个马尔科夫模型。图二展示了一层通道数为5的卷积层的剪枝过程。其中S1表示保留第一个通道,S2表示保留第二个通道,以此类推。T表示剪枝完毕。概率p则为转移概率,通过可学习的参数计算得到,后文中会详细介绍。
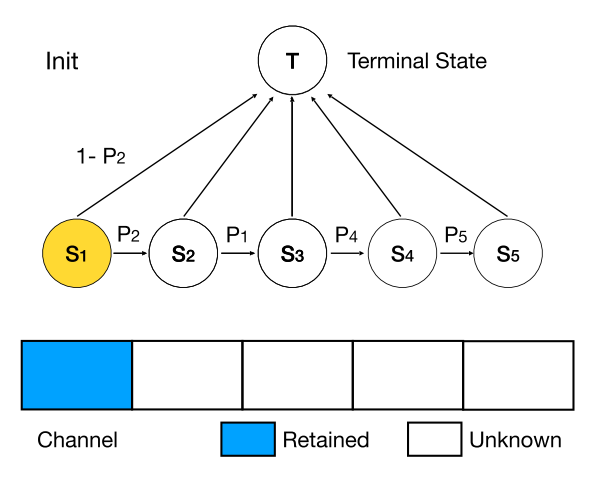
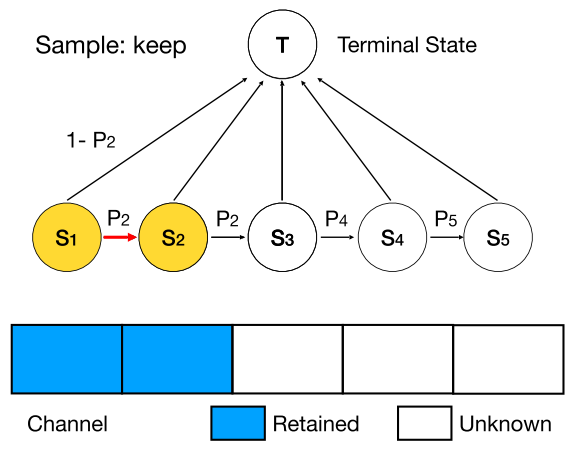
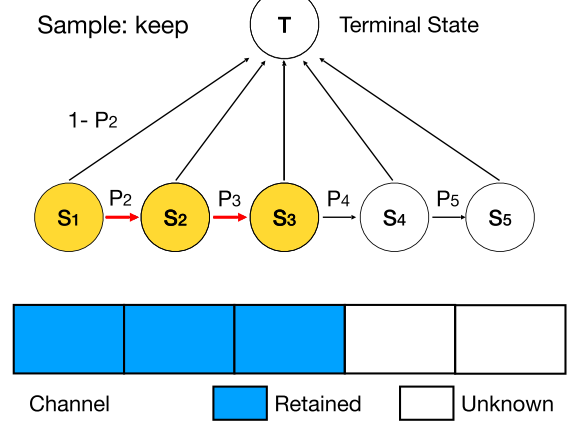
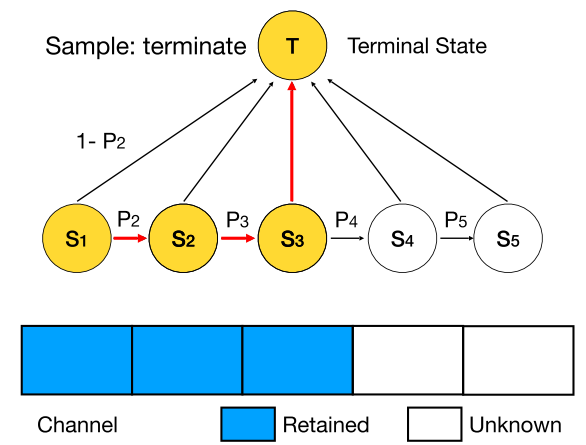
(1)优化剪枝空间
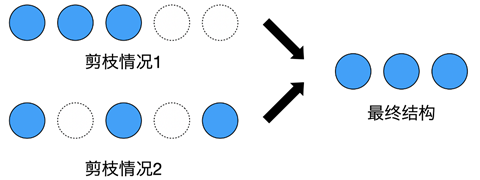
在传统的剪枝方法中,会为每个通道计算“重要性”来决定是否保留它。而当我们把模型剪枝看作模型结构搜索问题后,不同模型的区别则在于每一层的通道数量。如果仍然每个通道单独判断,就会产生同样的结构,造成优化困难。如图三所示:情况1中,最后两个通道被剪掉,情况2中,第2个和第4个通道被剪掉,而这两种情况都会产生3个通道的卷积层,使剪枝空间远大于实际网络个数。
因此,DMCP采用保留前k个通道的方式,大大缩小了剪枝空间。
(2)建模剪枝过程
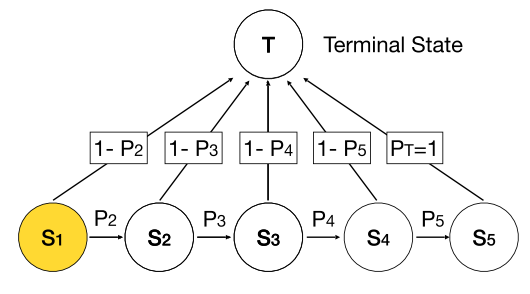

其中pk为马尔科夫模型中的转移概率。这样,通过在优化完毕后的马尔可夫模型上采样就可以得到相应的剪枝后的模型。
(3)学习转移概率
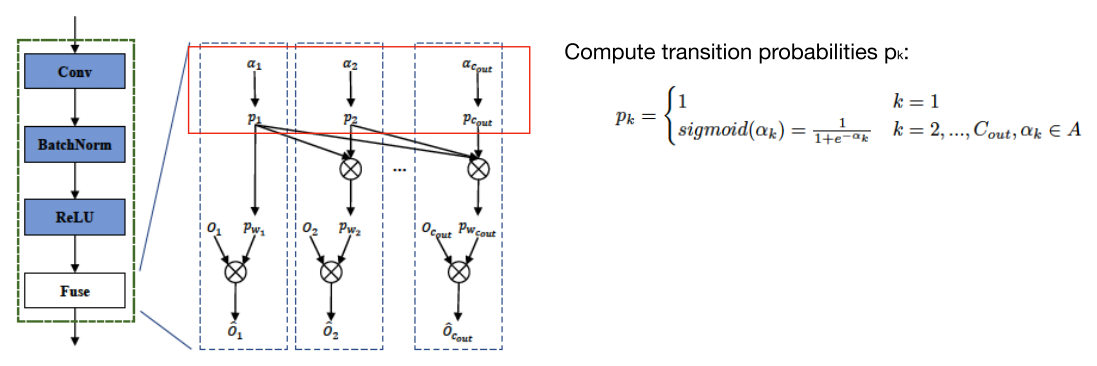
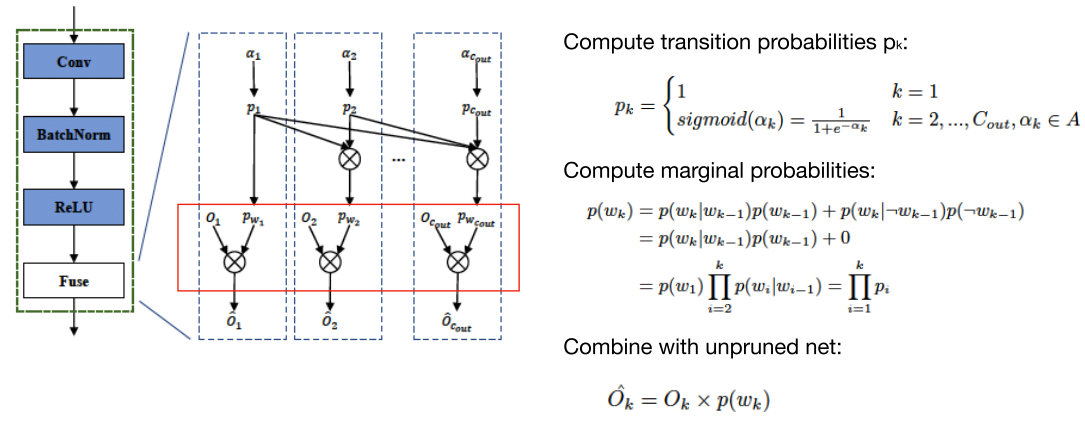
((p_k) 是转移概率,(p_{w1}) 是边缘概率)
(4)训练流程
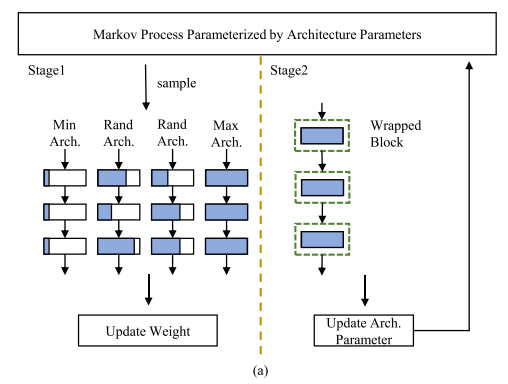
DMCP的训练可以分为两个阶段:训练原模型和更新马尔科夫模型。这两个阶段是交替进行来优化的。
阶段一,训练原模型。
在每一轮迭代过程中,利用马尔科夫过程采样两个随机结构,同时也采样了最大与最小的结构来保证原模型的所有参数可以充分训练。所有采样的结构都与原模型共享训练参数,因此所有子模型在任务数据集上的精度损失函数得到的梯度都会更新至原模型的参数上。
阶段二,更新马尔科夫模型
在训练原模型后,通过前文中所描述的方法将马尔科夫模型中的转移概率和原模型结合,从而可以利用梯度下降的方式更新马尔科夫模型的参数,其损失函数如下:
Experiments
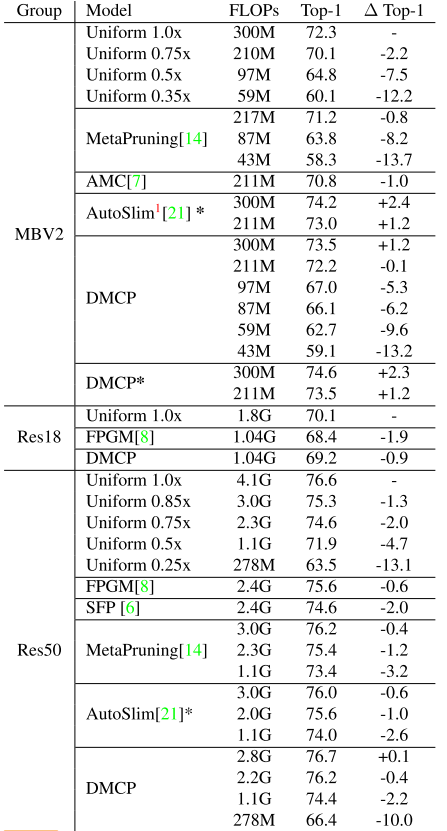
Conclusion
The proposed method is differentiable by modeling the channel pruning as the Markov process, thus can be optimized with respect to task loss by gradient descent.
Summary
Reference
【CVPR 2020 Oral丨DMCP: 可微分的深度模型剪枝算法解读】https://zhuanlan.zhihu.com/p/146721840
【Soft Filter Pruning(SFP)算法笔记】https://blog.csdn.net/u014380165/article/details/81107032