Light OJ 1005

题目大意：

给你一个N和K要求确定有多少种放法，使得没有两个车在一条线上。

N*N的矩阵， 有K个棋子。

题目分析：

我是用DP来写的，关于子结构的考虑是这样的。

假设第n*n的矩阵放k个棋子那么，这个推导过程如下。

 

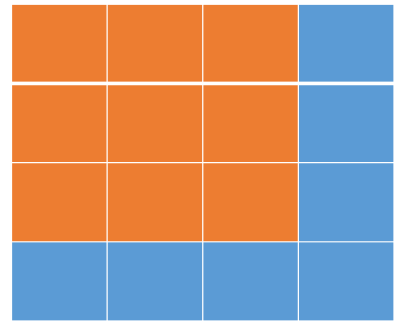
当我们们第n*n的矩阵的时候可以考虑第(n-1)*(n-1)的矩阵经过哪些变换可以变成n*n的。

如上图蓝色方格。我们加入蓝色方格之后，矩阵就会增大一圈。

1.加入我们蓝色方格不放置棋子。 dp[n-1][k]

2.加入蓝色方格放置一枚棋子，那么我们其实有三种位置可以放置：（1）右侧蓝色（2）底侧蓝色（3）有下角。

对于每一种情况我们放置方格的位置可以有 n-k, 个故： (2*(n-k) + 1) * dp[n-1][k-1]

3.放置两个棋子， 那么放置两个棋子的话肯定不能在左下角放置。故： （n-k）*(n-k)*dp[n-1][k-2]

 

===========================================================================================

 

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<vector>
#include<map>
using namespace std;
typedef unsigned long long LL;
const int INF = 1e9+7;
const int maxn = 105;
const int MOD = 9973;
LL dp[maxn][905];
void solve()
{
    for(int i=0; i<=30; i++)
        dp[i][0] = 1;

    for(int i=1; i<=30; i++)
    for(int j=1; j<=i; j++)
    {
        dp[i][j] = dp[i-1][j] + (2*(i-j)+1) * dp[i-1][j-1];
        if(j-2 >= 0)
            dp[i][j] += (i-j+1)*(i-j+1) * dp[i-1][j-2];
    }
}

int main()
{
    int T, n, k, cas = 1;
    solve();
    scanf("%d", &T);

    while(T--)
    {
        scanf("%d %d", &n, &k);
        printf("Case %d: %llu
",cas++, dp[n][k]);
    }
    return 0;
}