软件测试的艺术(读书笔记2)

下面开始本书第二部分的读书笔记部分

第二部分 软件测试基础

　　包括第4章 测试用例设计；第5章 单元（模块）测试；第6章 更高级别的测试

第4章 测试用例设计

 　　由于时间和成本约束，能够设计和生成一套能够发现最多错误的测试用例就变得很重要。

　　本章主要介绍常见的黑盒和白盒方法来设计测试用例，当让在实际的测试中，应综合两种方法进行用例的设计。首先使用黑盒方法设计测试用例，然后视情况用白盒测试方法进行测试用例的补充。

　　1、黑盒测试

　　黑盒测试的目的是找出程序不符合规格说明书的地方，主要包括等价划分方法、边界值方法、因果图（不常用）。

　　1）等价类划分方法

　　将程序输入范围进行划分为有限的等价类，测试等价类就等同于测试该类的其他数据。等价类划分方法设计测试用例有两个步骤：（1）确定等价类；（2）生成测试用例；

　　（1）确定等价类

　　　　首先，选取每一个输入条件（程序规格说明书中一个句子或短语），将其划分为两个或更多的组（类）；然后，将划分后的每一组分成有效等价类和无效等价类

外部输入条件	有效等价类	无效等价类
数量可以是从1到999（取值范围）	1<数量<999	数量<1,数量>999
汽车可登记一至六名车主（取值个数）	有1到6个车主	没有车主，或车主多于6个
交通工具必须是公共汽车，卡车，出租车，火车或摩托车（输入值的集合）	输入交通工具的一个	拖车
标识符的第一个字符必须是字母（规定“必须是”的情况）	首字符是字母	首字符不是字母

　　（2）生成测试用例

　　　　1.为每个等价类设置编号

　　　　2.编写测试用例，覆盖更多的未覆盖的有效等价类

　　　　3.编写测试用例，覆盖未覆盖的无效等价类

　　2）边界值分析方法

　　边界条件，指输入和输出等价类中那些恰好处于边界、或超出边界、或在边界以下的状态。和等价类划分不用在于

用例方法	数据选取	输入/输出条件
等价类划分	任意一个元素均可	仅关注输入条件
边界值分析	每个边界元素	输入输出均关注

　　关于边界条件的通用指南

外部条件	边界条件	例子
规定输入值范围	针对刚刚越界情况设计无效输入设计用例	范围是-1.0到+1.0，应根据-1.0，1.0，-1，001和-1.001设计
规定输入值数量	针对最小数量，最大数量，比最小数量少一个，比最小数量多一个设计用例	输入文件可容纳1-255条记录，应根据0，1，255，256设计
规定输出值范围	针对刚刚越界情况设计无效输出设计用例	某程序扣除金额在￥0.00到￥1165.25，应设计扣除在￥0.00和￥1165.25情况，同时设计导致扣除金额为负数或超出￥1165.25的用例
规定输出值数量	针对最小数量，最大数量，比最小数量少一个，比最小数量多一个设计用例	信息检索系统需要检索数量不超4条的记录，应设计显示条数为0条，1条和4条的记录，还应设计显示5条的用例
输入输出是一个有序序列（顺序文件，线性列表）	该序列的第一个和最后一个元素

　　3）因果图方法

　　边界值分析和等价类划分并不会对输入条件的组合进行分析，而因果图则可以。因果图的目的是用一个系统方法选择出高效测试用例集。有些商用软件可以帮助，用到时可以了解。

　　2、白盒测试

 　　白盒测试主要关注源代码中程序逻辑和结构是否执行成功。主要包括，语句覆盖，判定覆盖，条件覆盖，判定/条件覆盖，多重条件覆盖。

　　1）语句覆盖

　　定义：将程序中的每条语句至少执行一次。　　

public void foo(int a, int b, int x) {
    if (A>1 && B==0) {
        X = X/A;
    }
    if (A==2 || X>1) {
        X=X+1;
    }
}

 　　如果A=2，B=0，X=3，每条语句被执行一次，但并没有发现什么错误，没有什么用处。

　　2）判定覆盖或分支覆盖

　　定义：编写足够测试用例，使得每一个判断都至少有一个为真和为假的输出结果。

public void foo(int a, int b, int x) {
    if (A>1 && B==0) {
        X = X/A;
    }
    if (A==2 || X>1) {
        X=X+1;
    }
}

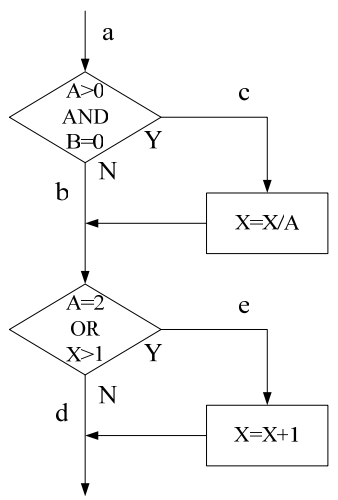
　　如下图所示，如果按照判定覆盖定义去设计测试用例，只需要设计测试用例，涵盖路径ace和abd，或者涵盖路径acd和abe就可以满足要求。如果选择acd和abe路径，测试用例的输入A=3，B=0，X=3和A=2，B=1，X=1。如果第二个判断存在错误，测试用例是无法发现错误。

　　　　　　 

　　3）条件覆盖

　　定义：编写足够的测试用例，将一个判断中的每个条件的所有可能结果至少执行一次。条件覆盖比判定强，因为条件覆盖会使判断中每个条件都取两个结果（真和假）。

　　比如在a点处有两个条件A>1和B=0，那么需要设计测试用例，能在a点处出现A>1，A<=1，B=0和B<>0的情况。

　　虽然条件覆盖能够满足判断中条件的真假，但是对判断语句的真假不能满足。所以需要将判定覆盖和条件覆盖进行结合。

　　4）判定/条件覆盖

　　定义：设计足够的测试用例，将判断中每个条件的所有可能的结果至少执行一次，且将每个判断的所有可能的结果至少执行一次。

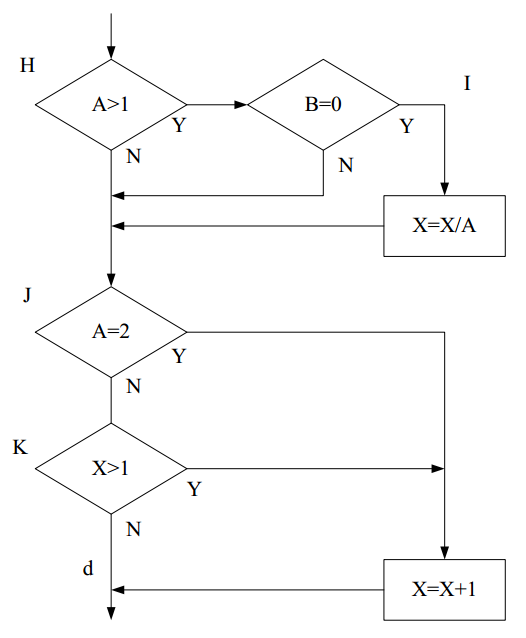
　　如下图所示将判定和条件覆盖进行结合，但是因为A>1和B=0是相“与”的关系，A=2和X>1是相“或”的关系，在编译器中，如果“与”表达式中有个条件为“假”，则不会执行后续条件；如果“或”表达式中有个条件为“真”，不会执行后续条件。程序不能执行H中为假的分支，以及判断K中为真的分支。所以判定/条件覆盖可能不会发现逻辑表达式中的错误。　

　

　　5）多重条件覆盖

　　定义：编写足够多测试用例，将每个判定中的所有可能的条件结果的组合，以及所有的入口点都至少执行一次。存在循环情况下，多重条件覆盖准则所需测试用例数量远小于其路径数量。

    if(x==y && length(z)==0 && FLAG) {
        j = 1;
    }
    else {
        i = 1;
    }

 　对以上判定语句进行分析，每个条件有以下三种情况

　　　　1.x==y，x!=y

　　　　2.length(z) ==0，length(z)<>0

　　　　3.FLAG，！FLAG

　　从三种情况进行条件组合，有8个测试用例

　　　　1.x==y，length(z) ==0，FLAG

　　　　2.x==y，length(z) ==0，！FLAG

　　　　3.x==y，length(z)<>0，FLAG

　　　　4.x==y，length(z)<>0，！FLAG

　　　　5.x！=y，length(z) ==0，FLAG

　　　　6.x！=y，length(z) ==0，！FLAG

　　　　7.x！=y，length(z)<>0，FLAG

　　　　8.x！=y，length(z)<>0，！FLAG

　　3、错误猜测方法

　　是一种依赖直觉的非正规过程。基本思想是列举出可能犯的错误或错误易发情况的清单，然后根据清单来编写测试用例。这种方法很难系统化，严重依赖于个人能力。

　　假设测试一个排序程序，应探讨如下情况测试用例

　　1.输入列表为空

　　2.输入列表仅包含一个条目

　　3.输入列表所有条目的值都相等

　　4.输入列表已经排过序

　　综上，测试用例的设计，首先，可以根据规格说明书文档，通过黑盒方法中的有效等价类和边界值分析方法进行设计；然后，根据测试经验用错误猜测方法增加更多的测试用例；最后，可以检查程序的逻辑结构，使用判定覆盖、条件覆盖、判定/条件覆盖或多重条件覆盖准则进行用例设计。