BST

  二叉查找树（Binary Search Tree），（又：二叉搜索树，二叉排序树）它或者是一棵空树，或者是具有下列性质的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
• 它的左、右子树也分别为二叉排序树。

  二叉搜索树作为一种经典的数据结构，它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势；所以应用十分广泛，例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。

存储结构

BSTNode.h

template<typename T>
class BSTNode{
public:
    T e;    //节点元素
    BSTNode<T>*left;   //左节点
    BSTNode<T>*right;  //右节点
    
public:
    BSTNode(T E):e(E),left(nullptr),right(nullptr){}	//初始化
};

BST.h

class BST {
private:
    BSTNode<T> *root;   //根节点
    int size;   //大小
public:
};

二叉查找树也是二叉树，所以存储结构和二叉树一样。

算法实现

添加

/*------------------------------------------------------------------*/
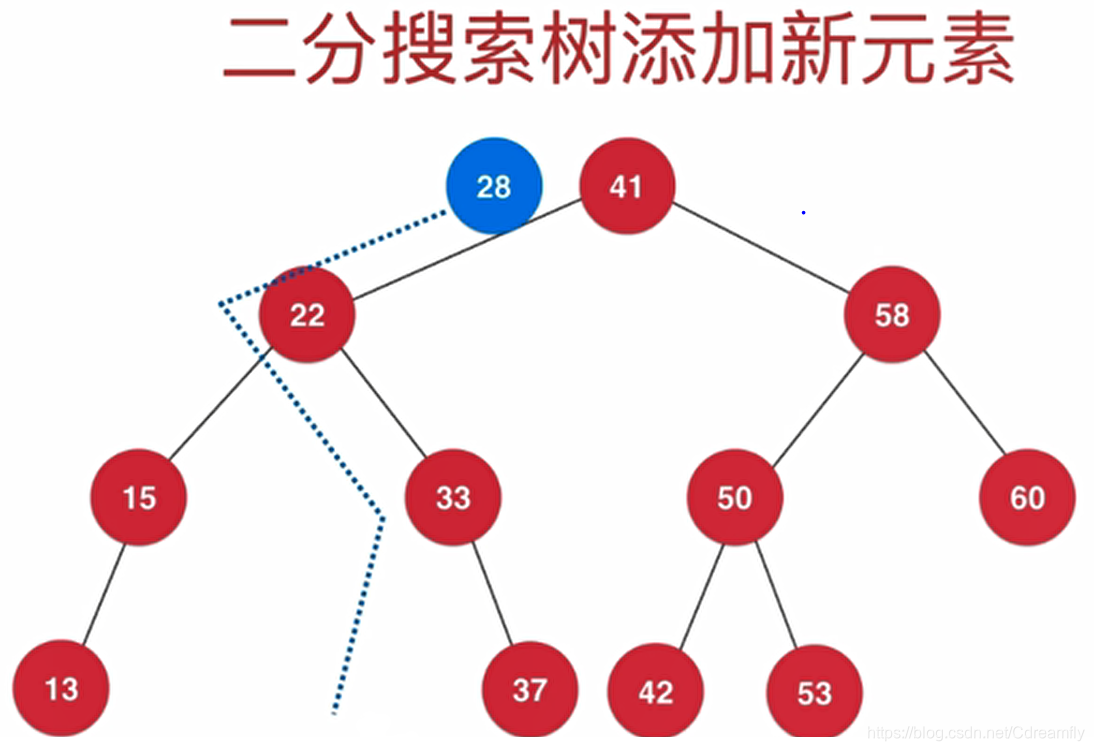
private:
    //返回插入新节点后二分搜索树的根
    BSTNode<T> *add(BSTNode<T> *node, T e) {
        if (node == nullptr) {  //如果结点为空
            ++size;     //大小+1
            return new BSTNode<T>(e);   //插入元素e返回新节点
        }
        if (node->e > e) {  //如果要插入的节点值小于当前节点元素
            node->left = add(node->left, e);    //第归左子树直到为空返回新节点为当前节点的左孩子
        } else if (node->e < e) {   //如果要插入的节点值大于当前节点元素
            node->right = add(node->right, e);  //第归右子树直到为空返回新节点为当前节点的右孩子
        }
        return node;    //返回原节点
    }

public:
    void add(T e) { //添加节点
        root = add(root, e);    //添加新节点传入根结点和元素并返回新的根结点
    }
/*------------------------------------------------------------------*/

我的BST不包含重复元素，如果想要包含重复元素的话，只需要定义：

• 左子树小于等于节点；
• 或者右子树大于等于节点；

查询

/*------------------------------------------------------------------*/
private:
    bool contains(BSTNode<T> *node, T e) {  //判断是否有元素e
        if (node == nullptr)return false;   //如果节点为空，则返回false
        if (node->e == e)return true;   //如果要找的的元素等于节点元素e，则返回true
        else if (node->e > e) { //如果要找的元素小于节点元素
            return contains(node->left, e); //则第归当前节点的左子树
        } else { // if(node->e<e)   //如果要找的元素大于节点元素
            return contains(node->right, e);    //则第归当前节点的右子树
        }
    }

public:
    bool contains(T e) {    //判断是否有元素e
        return contains(root, e);
    }
/*------------------------------------------------------------------*/

深度优先遍历

• 前续遍历：

/*------------------------------------------------------------------*/
private:
    void preOrder(BSTNode<T> *node){//第归前序遍历
        if (node == nullptr)return; //如果节点为则空返回
        std::cout << node->e << std::endl;//打印节点元素
        preOrder(node->left);   //第归当前节点左子树
        preOrder(node->right);  //第归当前节点右子树
    }

public:
    void preOrder(){//第归前序遍历
        preOrder(root);
    }
/*------------------------------------------------------------------*/

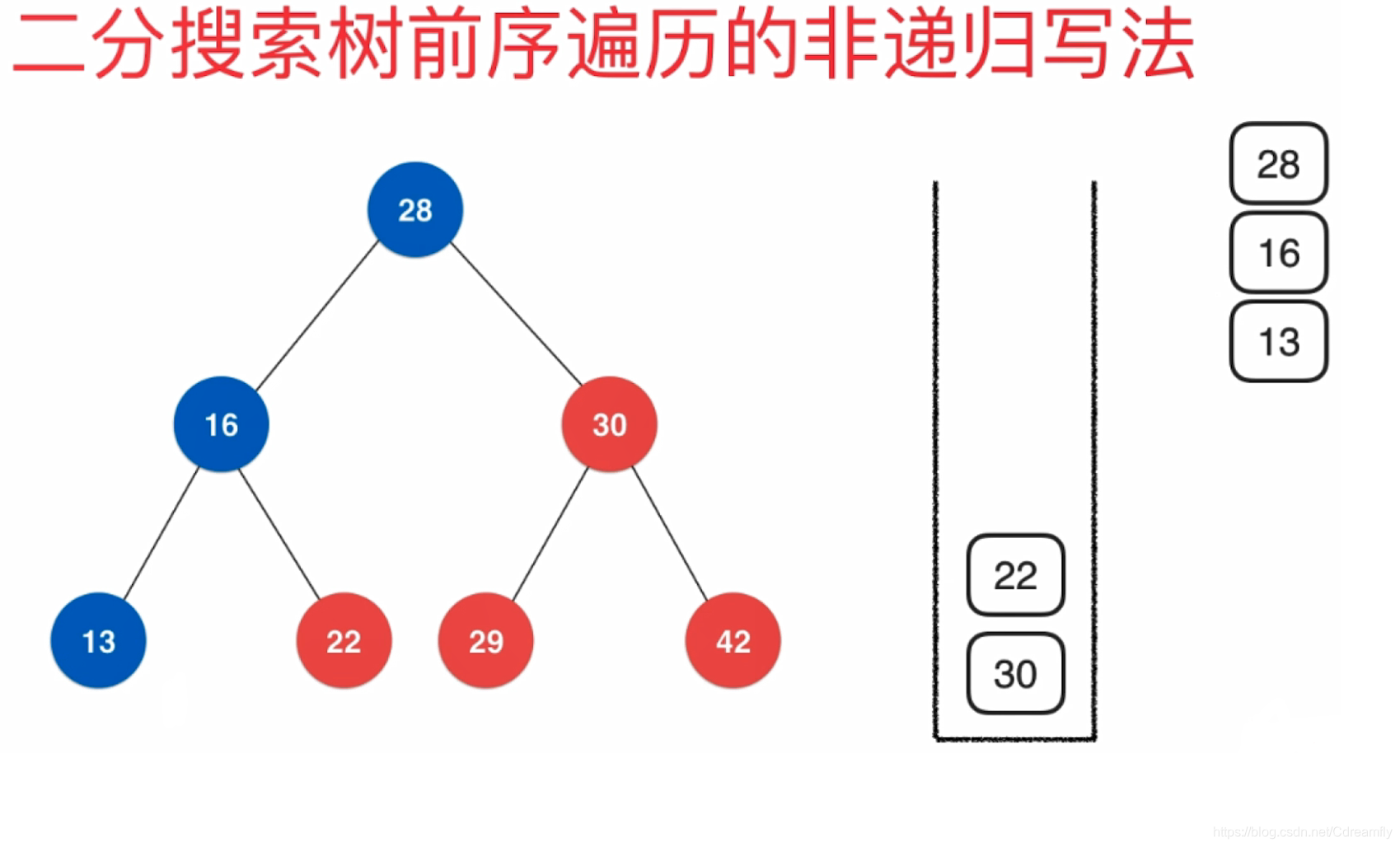
//非递归前序遍历 深度优先遍历
    void preOrderNR() {
        std::stack<BSTNode<T> *> s;//创建一个栈
        s.push(root);//根节点入栈
        while (!s.empty()) {    //如果栈为空，则停止循环
            BSTNode<T> *cur = s.top();  //创建一个节点暂存栈顶节点
            std::cout << cur->e << " "; //打印栈顶节点
            s.pop();    //出栈
            if (nullptr != cur->right) {    //如果栈顶节点右节点不为空
                s.push(cur->right); //栈顶节点右节点如栈
            }
            if (nullptr != cur->left) {     //如果栈顶节点左节点不为空
                s.push(cur->left);  //栈顶节点左节点如栈
            }
        }
        std::cout << std::endl;
    }

• 中续遍历

/*------------------------------------------------------------------*/
private:
    void inOrder(BSTNode<T> *node) {    //第归中序遍历
        if (node == nullptr)return;
        inOrder(node->left);
        std::cout << node->e << std::endl;
        inOrder(node->right);
    }

public:
    void inOrder() {    //第归中序遍历
        inOrder(root);
    }
/*------------------------------------------------------------------*/

//非递归中序遍历
    void inOrderNR() {
        std::stack<BSTNode<T> *> s; //创建一个栈
        BSTNode<T> *cur = root;     //当前节点为根节点
        while (!s.empty() || nullptr != cur) {  //如果栈为空或当前节点为空
            //树的左边一列入栈
            while (nullptr != cur) {
                s.push(cur);
                cur = cur->left;
            }
            if (!s.empty()) {   //如果栈不为空
                cur = s.top();  //当前节点为栈顶
                std::cout << cur->e << " ";//打印节点元素
                s.pop();    //出栈
                cur = cur->rigfht;   //当节点赋值为当前节点的右节点
            }
        }
        std::cout << std::endl;
    }

也叫排序遍历，它会有序打印二分搜索树。

• 后续遍历

/*------------------------------------------------------------------*/
private:
    void postOrder(BSTNode<T> *node) {//第归后续遍历
        if (node == nullptr)return;
        postOrder(node->left);
        postOrder(node->right);
        std::cout << node->e << std::endl;
    }

public:
    void postOrder() {  //后续遍历
        postOrder(root);
    }
/*------------------------------------------------------------------*/

void postOrderNR(){ //非第归后续遍历
        std::stack<BSTNode<T>*>s;   //创建一个栈
        BSTNode<T>*cur = root;  
        BSTNode<T>*temp;
        while(nullptr != cur || !s.empty()){
            //树的左边一列入栈
            while(nullptr != cur){
                s.push(cur);
                cur = cur ->left;
            }
            if(!s.empty()){ //如果栈不为空
                cur = s.top();  //当前节点为栈顶
                if(cur->right == temp || nullptr ==  cur->right){   //如果当前节点为暂存节点的父节点或当前节的右节点为空
                    std::cout<<cur->e<<" "; //打印当前节点元素
                    s.pop();    //出栈
                    temp = cur; //暂存当前节点
                    cur = nullptr;  //cur赋值为空
                } else{ 
                    cur = cur->right;   //否则遍历右节点
                }
            }
        }
        std::cout<<std::endl;
    }

后续遍历，它会先深入到树的底部从下向上遍历，所以后续遍历适用于释放内存。

广度优先遍历

• 层次遍历

/*------------------------------------------------------------------*/
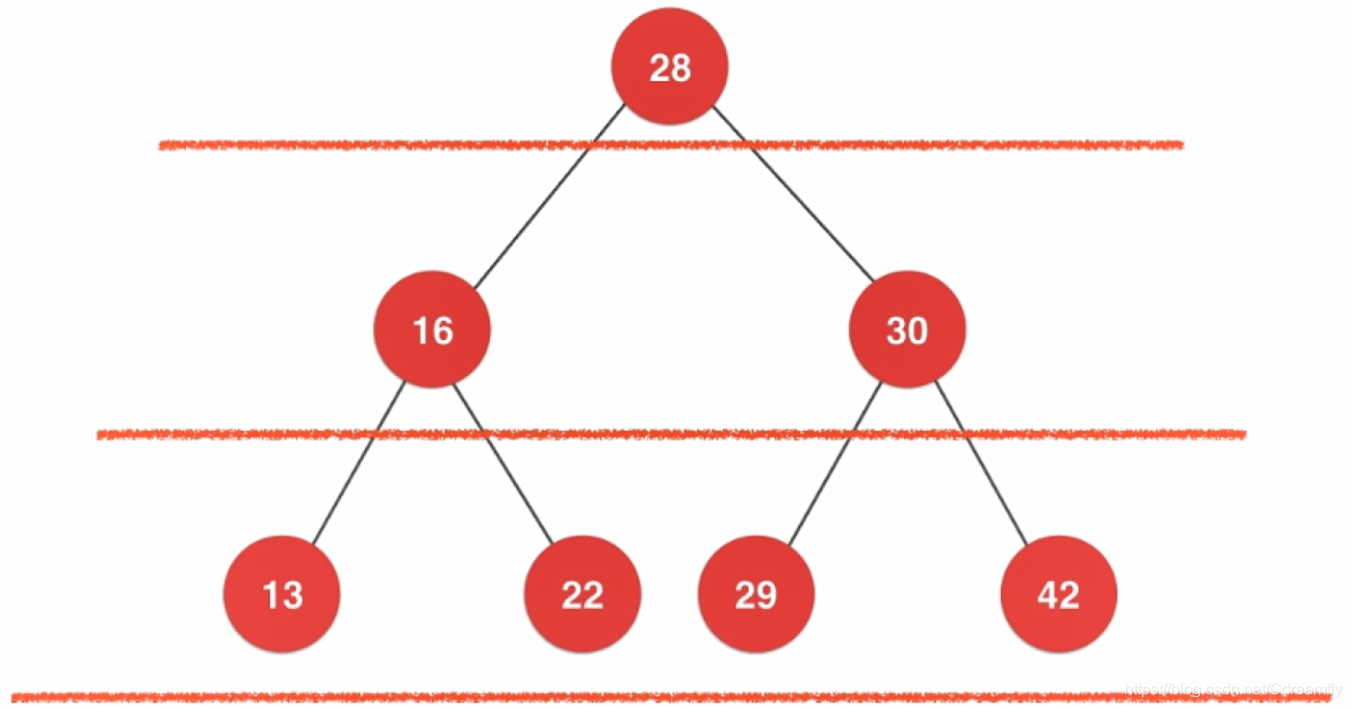
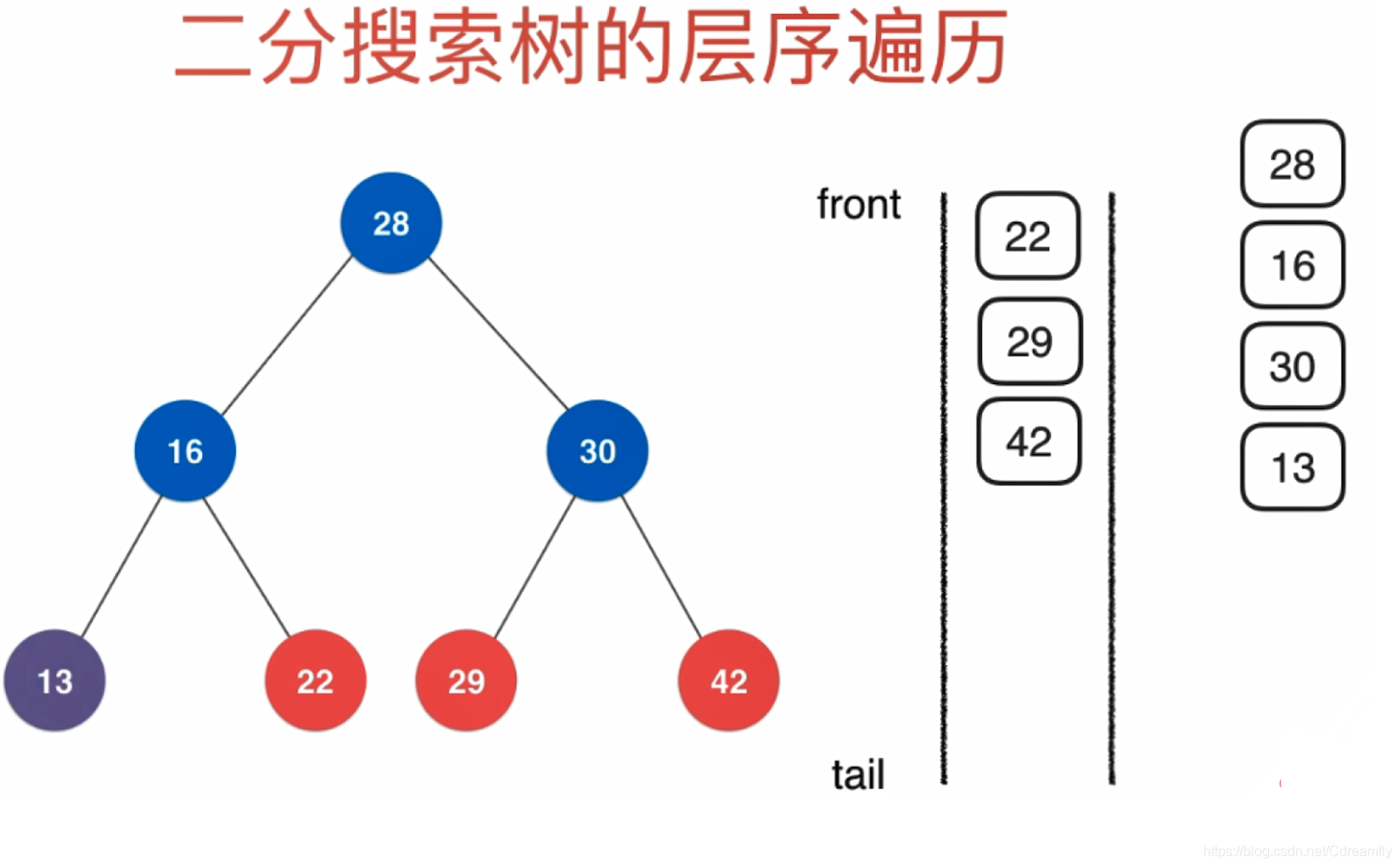
public:
    void levelOrder(){
        std::queue<BSTNode<T>*>q;   //创建一个队列
        q.push(root);   //根结点如对
        while(!q.empty()){  //如果队列不为空
            BSTNode<T>*cur = q.front();    //取出对头节点
            q.pop();    //出队
            std::cout<<cur->e<<" "; //打印对头节点元素
            if(nullptr != cur->left){   //如果当前节点的左孩子不为空
                q.push(cur->left);  //则当前节点的左孩子入队
            }
            if(nullptr !=cur->right){   //如果当前节点的右孩子不为空
                q.push(cur->right); //则当前节点的右孩子入队
            }
        }
        std::cout<<std::endl;
    }
/*------------------------------------------------------------------*/

层次遍历是从上向下遍历，适用于搜索策略上。

查找最大最小值

/*------------------------------------------------------------------*/
private:
    //返回最小值的节点
    BSTNode<T> *min(BSTNode<T> *node) {
        if (node->left == nullptr)  //二分搜索树最小值肯定是最左边的节点
            return node;
        return min(node->left);
    }
    //返回最大值的节点
    BSTNode<T> *max(BSTNode<T> *node) {
        if (node->right == nullptr) //二分搜索树最大值肯定是最右边的节点
            return node;
        return max(node->right);
    }

public:
    T minimun() {//返回最小值
        if (size > 0) return min(root)->e;
    }
    T maximun() {//返回最大值
        if (size > 0) return max(root)->e;
    }
/*------------------------------------------------------------------*/

根据BST的特性，最小值，一定在树的最左边节点，最大值，一定在树的最右边节点。

删除最大最小值

/*------------------------------------------------------------------*/
private:
    //删除以node为根的二分搜索树的最小节点
    //返回删除节点后新的二分搜搜索树的根结点
    BSTNode<T> *removeMin(BSTNode<T> *node) {
        if (node->left == nullptr) { //如果当前节点左孩子为空
            BSTNode<T> *rightNode = node->right;    //则暂存当前节点的右孩子
            delete node;    //删除当前节点
            size--; //个数-1
            return rightNode;   //返回被删除节点的右孩子
        }
        node->left = removeMin(node->left); //第归节点的左孩子，把返回的右孩子放入上一节点的左孩子
        return node;    //返回根结点
    }
    //删除以node为根的二分搜索树的最大节点
    //返回删除节点后新的二分搜搜索树的根结点
    BSTNode<T> *removeMax(BSTNode<T> *node) {
        if (node->right == nullptr) {
            BSTNode<T> *leftNode = node->left;
            delete node;
            size--;
            return leftNode;
        }
        node->right = removeMax(node->right);
        return node;
    }

public:
    T removeMin() { //删除最小值并返回最小值
        T ret = minimun();
        root = removeMin(root);
        return ret;
    }
    T removeMax() { //删除最大值并返回最大值
        T ret = maximun();
        root = removeMax(root);
        return ret;
    }
/*------------------------------------------------------------------*/

因为最大最小值都是在树的叶子节点，这个最小值叶子只有右孩子可能会有子树，所以删除叶子节点时无论它有没有右孩子，都把它的右孩子放到它父节点的左孩子上。
注意：空也是一个二叉树；

删除任意值

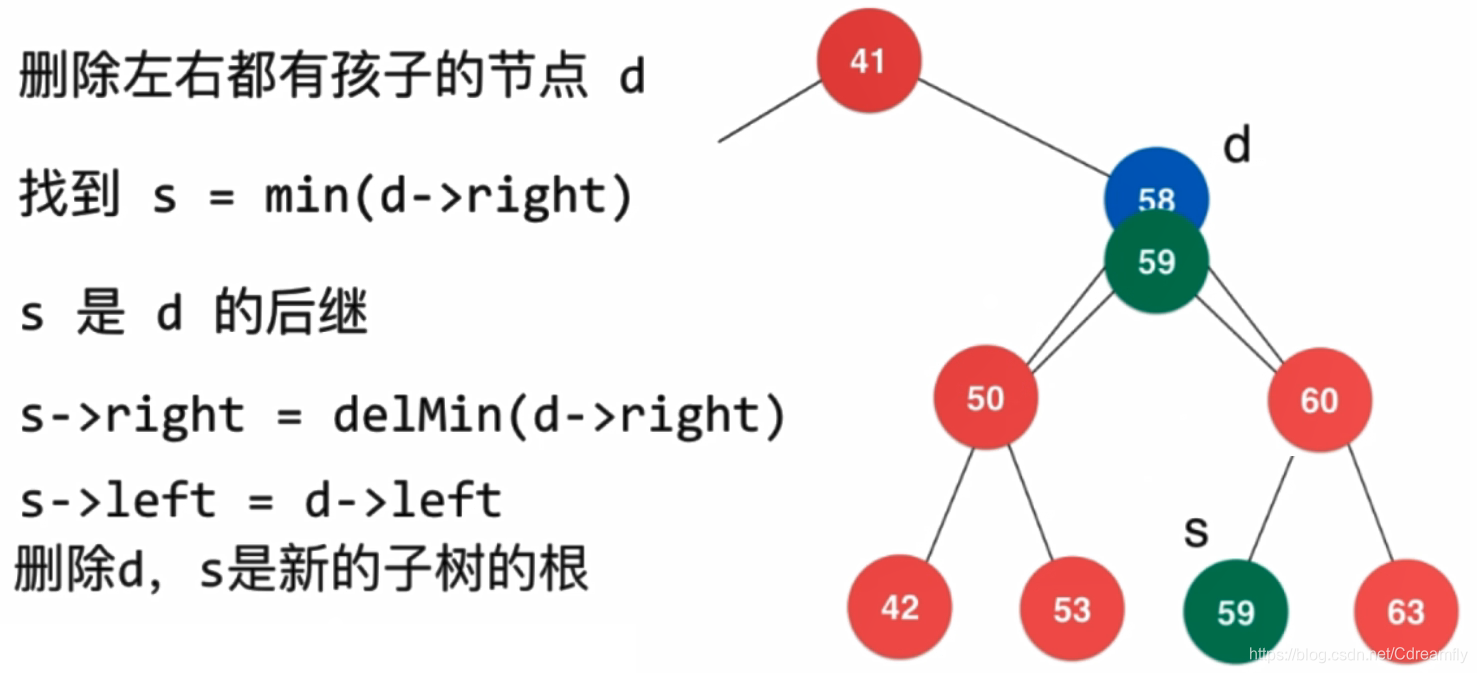
前驱法同理

/*------------------------------------------------------------------*/
private:
    //删除元素e 后继法
    BSTNode<T>* RRemove(BSTNode<T>*node,T e)
    {
        if(nullptr == node)return nullptr;  //如果节点为空，则返回空
        if(e<node->e)   //如果要删除元素小于当前节点元素
        {
            node->left = RRemove(node->left,e); //当前节点的左孩子赋值为，第归当前节点的左孩子返回当节点前左孩子的右孩子
            return node;    //返当根节点
        }else if(e>node->e){//如果要删除元素大于当前节点元素
            node->right = RRemove(node->right,e);//当前节点的右孩子赋值为，第归当前节点的右孩子返回当前节点右孩子的左孩子
            return node;    //返回根节点
        } else { //e == node->e 如果要删除元素等于当前节点元素
            if (nullptr == node->left) {    //如果当前节点没有左孩子
                BSTNode<T> *rightNode = node->right;    //就暂存当前节点的右孩子
                delete node;    //删除当前节点
                --size; //大小-1
                return rightNode;   //返回当前节点的右孩子
            }
            if (nullptr == node->right) {   //如果当前节点没有左孩子
                BSTNode<T> *leftNode = node->left;  //就暂存当前节点的左孩子
                delete node;    //删除当前节点
                --size; //大小-1
                return leftNode;    //返回当前节点的左孩子
            }
            //如果不为空就把离要删除节点最近的比节点要大的节点拿过来，换成它。
            BSTNode<T> *successor = new BSTNode<T>(min(node->right)->e);    //创建一个节点把要删除节点的右子树中最小值给新建节点
            successor->right = removeMin(node->right);  //新建节点的右孩子指向，删除当前节点的右子树中的最小节点并返回这个根结点。
                                                        // removeMin过程中size已经-1，所以不需要再-1
            successor->left = node->left;   //新建节点的左孩子指向要删除节点的左孩子
            node->left = node->right = nullptr; //把要删除节点左右孩子指向空
            delete node;    //删除要删除节点
            return successor;   //返回新建节点给上一级
        }
    }
    //删除元素e 前驱法
    BSTNode<T>* LRemove(BSTNode<T>*node,T e)
    {
        if(nullptr == node)return nullptr;
        if(node->e>e)
        {
            node->left = LRemove(node->left,e);
            return node;
        }else if(node->e<e){
            node->right = LRemove(node->right,e);
            return node;
        } else{ //node->e == e
            if(nullptr == node->left){
                BSTNode<T>*rightNode = node->right;
                delete node;
                --size;
                return rightNode;
            }
            if(nullptr == node->right){
                BSTNode<T>*leftNode = node->left;
                delete node;
                --size;
                return leftNode;
            }
            BSTNode<T>*precursor = new BSTNode<T>(min(node->left)->e);
            precursor->left = removeMin(node->left);
            precursor->right = node->right;
            node->left = node->right = nullptr;
            delete node;
            return precursor;
        }
    }

public:
    void RRemove(T e)//删除任意元素e前驱法
    {
        root = RRemove(root,e);
    }
    void LRemove(T e)//删除任意元素e后继法
    {
        root = LRemove(root,e);
    }
/*------------------------------------------------------------------*/

代码清单

#ifndef C___BST_H
#define C___BST_H
#include <stack>
#include <queue>

template<typename T>
class BSTNode{
public:
    T e;    //节点元素
    BSTNode<T>*left;   //左节点
    BSTNode<T>*right;  //右节点
    
public:
    BSTNode(T E):e(E),left(nullptr),right(nullptr){}
};

template<typename T>
class BST {
private:
    BSTNode<T> *root;   //根节点
    int size;   //大小
/*------------------------------------------------------------------*/
private:
    //返回插入新节点后二分搜索树的根
    BSTNode<T> *add(BSTNode<T> *node, T e) {
        if (node == nullptr) {  //如果结点为空
            ++size;     //大小+1
            return new BSTNode<T>(e);   //插入元素e返回新节点
        }
        if (node->e > e) {  //如果要插入的节点值小于当前节点元素
            node->left = add(node->left, e);    //第归左子树直到为空返回新节点为当前节点的左孩子
        } else if (node->e < e) {   //如果要插入的节点值大于当前节点元素
            node->right = add(node->right, e);  //第归右子树直到为空返回新节点为当前节点的右孩子
        }
        return node;    //返回原节点
    }

public:
    void add(T e) { //添加节点
        root = add(root, e);    //添加新节点传入根结点和元素并返回新的根结点
    }
/*------------------------------------------------------------------*/
private:
    bool contains(BSTNode<T> *node, T e) {  //判断是否有元素e
        if (node == nullptr)return false;   //如果节点为空，则返回false
        if (node->e == e)return true;   //如果要找的的元素等于节点元素e，则返回true
        else if (node->e > e) { //如果要找的元素小于节点元素
            return contains(node->left, e); //则第归当前节点的左子树
        } else { // if(node->e<e)   //如果要找的元素大于节点元素
            return contains(node->right, e);    //则第归当前节点的右子树
        }
    }

public:
    bool contains(T e) {    //判断是否有元素e
        return contains(root, e);
    }
/*------------------------------------------------------------------*/
private:
    void preOrder(BSTNode<T> *node){//第归前序遍历
        if (node == nullptr)return; //如果节点为则空返回
        std::cout << node->e << std::endl;//打印节点元素
        preOrder(node->left);   //第归当前节点左子树
        preOrder(node->right);  //第归当前节点右子树
    }

public:
    void preOrder(){//第归前序遍历
        preOrder(root);
    }

    //非递归前序遍历 深度优先遍历
    void preOrderNR() {
        std::stack<BSTNode<T> *> s;//创建一个栈
        s.push(root);//根节点入栈
        while (!s.empty()) {    //如果栈为空，则停止循环
            BSTNode<T> *cur = s.top();  //创建一个节点暂存栈顶节点
            std::cout << cur->e << " "; //打印栈顶节点
            s.pop();    //出栈
            if (nullptr != cur->right) {    //如果栈顶节点右节点不为空
                s.push(cur->right); //栈顶节点右节点如栈
            }
            if (nullptr != cur->left) {     //如果栈顶节点左节点不为空
                s.push(cur->left);  //栈顶节点左节点如栈
            }
        }
        std::cout << std::endl;
    }
/*------------------------------------------------------------------*/
private:
    void inOrder(BSTNode<T> *node) {    //第归中序遍历
        if (node == nullptr)return;
        inOrder(node->left);
        std::cout << node->e << std::endl;
        inOrder(node->right);
    }
    //也叫排序遍历，它会有序打印二分搜索树
public:
    void inOrder() {    //第归中序遍历
        inOrder(root);
    }
    //非递归中序遍历
    void inOrderNR() {
        std::stack<BSTNode<T> *> s; //创建一个栈
        BSTNode<T> *cur = root;     //当前节点为根节点
        while (!s.empty() || nullptr != cur) {  //如果栈为空或当前节点为空
            //树的左边一列入栈
            while (nullptr != cur) {
                s.push(cur);
                cur = cur->left;
            }
            if (!s.empty()) {   //如果栈不为空
                cur = s.top();  //当前节点为栈顶
                std::cout << cur->e << " ";//打印节点元素
                s.pop();    //出栈
                cur = cur->rigfht;   //当节点赋值为当前节点的右节点
            }
        }
        std::cout << std::endl;
    }
/*------------------------------------------------------------------*/
private:
    void postOrder(BSTNode<T> *node) {//第归后续遍历
        if (node == nullptr)return;
        postOrder(node->left);
        postOrder(node->right);
        std::cout << node->e << std::endl;
    }

public:
    void postOrder() {  //后续遍历
        postOrder(root);
    }
    //后续遍历适用于析沟函数
    void postOrderNR(){ //非第归后续遍历
        std::stack<BSTNode<T>*>s;   //创建一个栈
        BSTNode<T>*cur = root;  
        BSTNode<T>*temp;
        while(nullptr != cur || !s.empty()){
            //树的左边一列入栈
            while(nullptr != cur){
                s.push(cur);
                cur = cur ->left;
            }
            if(!s.empty()){ //如果栈不为空
                cur = s.top();  //当前节点为栈顶
                if(cur->right == temp || nullptr ==  cur->right){   //如果当前节点为暂存节点的父节点或当前节的右节点为空
                    std::cout<<cur->e<<" "; //打印当前节点元素
                    s.pop();    //出栈
                    temp = cur; //暂存当前节点
                    cur = nullptr;  //cur赋值为空
                } else{ 
                    cur = cur->right;   //否则遍历右节点
                }
            }
        }
        std::cout<<std::endl;
    }
/*------------------------------------------------------------------*/
public:
    //层次遍历 广度优先遍历 适用于搜索
    void levelOrder(){
        std::queue<BSTNode<T>*>q;   //创建一个队列
        q.push(root);   //根结点如对
        while(!q.empty()){  //如果队列不为空
            BSTNode<T>*cur = q.front();    //取出对头节点
            q.pop();    //出队
            std::cout<<cur->e<<" "; //打印对头节点元素
            if(nullptr != cur->left){   //如果当前节点的左孩子不为空
                q.push(cur->left);  //则当前节点的左孩子入队
            }
            if(nullptr !=cur->right){   //如果当前节点的右孩子不为空
                q.push(cur->right); //则当前节点的右孩子入队
            }
        }
        std::cout<<std::endl;
    }
/*------------------------------------------------------------------*/
private:
    //返回最小值的节点
    BSTNode<T> *min(BSTNode<T> *node) {
        if (node->left == nullptr)  //二分搜索树最小值肯定是最左边的节点
            return node;
        return min(node->left);
    }
    //返回最大值的节点
    BSTNode<T> *max(BSTNode<T> *node) {
        if (node->right == nullptr) //二分搜索树最大值肯定是最右边的节点
            return node;
        return max(node->right);
    }

public:
    T minimun() {//返回最小值
        if (size > 0) return min(root)->e;
    }
    T maximun() {//返回最大值
        if (size > 0) return max(root)->e;
    }
/*------------------------------------------------------------------*/
private:
    //删除以node为根的二分搜索树的最小节点
    //返回删除节点后新的二分搜搜索树的根结点
    BSTNode<T> *removeMin(BSTNode<T> *node) {
        if (node->left == nullptr) { //如果当前节点左孩子为空
            BSTNode<T> *rightNode = node->right;    //则暂存当前节点的右孩子
            delete node;    //删除当前节点
            size--; //个数-1
            return rightNode;   //返回被删除节点的右孩子
        }
        node->left = removeMin(node->left); //第归节点的左孩子，把返回的右孩子放入上一节点的左孩子
        return node;    //返回根结点
    }
    //删除以node为根的二分搜索树的最大节点
    //返回删除节点后新的二分搜搜索树的根结点
    BSTNode<T> *removeMax(BSTNode<T> *node) {
        if (node->right == nullptr) {
            BSTNode<T> *leftNode = node->left;
            delete node;
            size--;
            return leftNode;
        }
        node->right = removeMax(node->right);
        return node;
    }

public:
    T removeMin() { //删除最小值并返回最小值
        T ret = minimun();
        root = removeMin(root);
        return ret;
    }
    T removeMax() { //删除最大值并返回最大值
        T ret = maximun();
        root = removeMax(root);
        return ret;
    }
/*------------------------------------------------------------------*/
private:
    //删除元素e 后继法
    BSTNode<T>* RRemove(BSTNode<T>*node,T e)
    {
        if(nullptr == node)return nullptr;  //如果节点为空，则返回空
        if(e<node->e)   //如果要删除元素小于当前节点元素
        {
            node->left = RRemove(node->left,e); //当前节点的左孩子赋值为，第归当前节点的左孩子返回当节点前左孩子的右孩子
            return node;    //返当根节点
        }else if(e>node->e){//如果要删除元素大于当前节点元素
            node->right = RRemove(node->right,e);//当前节点的右孩子赋值为，第归当前节点的右孩子返回当前节点右孩子的左孩子
            return node;    //返回根节点
        } else { //e == node->e 如果要删除元素等于当前节点元素
            if (nullptr == node->left) {    //如果当前节点没有左孩子
                BSTNode<T> *rightNode = node->right;    //就暂存当前节点的右孩子
                delete node;    //删除当前节点
                --size; //大小-1
                return rightNode;   //返回当前节点的右孩子
            }
            if (nullptr == node->right) {   //如果当前节点没有左孩子
                BSTNode<T> *leftNode = node->left;  //就暂存当前节点的左孩子
                delete node;    //删除当前节点
                --size; //大小-1
                return leftNode;    //返回当前节点的左孩子
            }
            //如果不为空就把离要删除节点最近的比节点要大的节点拿过来，换成它。
            BSTNode<T> *successor = new BSTNode<T>(min(node->right)->e);    //创建一个节点把要删除节点的右子树中最小值给新建节点
            successor->right = removeMin(node->right);  //新建节点的右孩子指向，删除当前节点的右子树中的最小节点并返回这个根结点。
                                                        // removeMin过程中size已经-1，所以不需要再-1
            successor->left = node->left;   //新建节点的左孩子指向要删除节点的左孩子
            node->left = node->right = nullptr; //把要删除节点左右孩子指向空
            delete node;    //删除要删除节点
            return successor;   //返回新建节点给上一级
        }
    }
    //删除元素e 前驱法
    BSTNode<T>* LRemove(BSTNode<T>*node,T e)
    {
        if(nullptr == node)return nullptr;
        if(node->e>e)
        {
            node->left = LRemove(node->left,e);
            return node;
        }else if(node->e<e){
            node->right = LRemove(node->right,e);
            return node;
        } else{ //node->e == e
            if(nullptr == node->left){
                BSTNode<T>*rightNode = node->right;
                delete node;
                --size;
                return rightNode;
            }
            if(nullptr == node->right){
                BSTNode<T>*leftNode = node->left;
                delete node;
                --size;
                return leftNode;
            }
            BSTNode<T>*precursor = new BSTNode<T>(min(node->left)->e);
            precursor->left = removeMin(node->left);
            precursor->right = node->right;
            node->left = node->right = nullptr;
            delete node;
            return precursor;
        }
    }

public:
    void RRemove(T e)//删除任意元素e前驱法
    {
        root = RRemove(root,e);
    }
    void LRemove(T e)//删除任意元素e后继法
    {
        root = LRemove(root,e);
    }
/*------------------------------------------------------------------*/
private:
    void generateDepthString(int depth) {
        for (int i = 0; i < depth; ++i) {
            std::cout << "--";
        }
    }

public:
    void generateBSTString(BSTNode<T> *node, int depth){
        if (node == nullptr){
            generateDepthString(depth);
            std::cout << "NULL" << std::endl;
            return;
        }
        generateDepthString(depth);
        std::cout << node->e << std::endl;
        generateBSTString(node->left, depth + 1);
        generateBSTString(node->right, depth + 1);
    }
    void print(){
        generateBSTString(root, 0);
    }
/*------------------------------------------------------------------*/    
public:
    BST() : root(nullptr), size(0) {}

    int getSize() const {      //返回当前树的大小
        return size;
    }

    bool isEmpty() const {  //判断当前树是否为空
        return size == 0;
    }
};

#endif //C___BST_H