BNU29139——PvZ once again——————【矩阵快速幂】

PvZ once again

Time Limit: 2000ms

Memory Limit: 65536KB

64-bit integer IO format: %lld      Java class name: Main

Prev 

Submit Status Statistics Discuss

 Next

Type: 

None

 

  None   Graph Theory       2-SAT       Articulation/Bridge/Biconnected Component       Cycles/Topological Sorting/Strongly Connected Component       Shortest Path           Bellman Ford           Dijkstra/Floyd Warshall       Euler Trail/Circuit       Heavy-Light Decomposition       Minimum Spanning Tree       Stable Marriage Problem       Trees       Directed Minimum Spanning Tree       Flow/Matching           Graph Matching               Bipartite Matching               Hopcroft–Karp Bipartite Matching               Weighted Bipartite Matching/Hungarian Algorithm           Flow               Max Flow/Min Cut               Min Cost Max Flow   DFS-like       Backtracking with Pruning/Branch and Bound       Basic Recursion       IDA* Search       Parsing/Grammar       Breadth First Search/Depth First Search       Advanced Search Techniques           Binary Search/Bisection           Ternary Search   Geometry       Basic Geometry       Computational Geometry       Convex Hull       Pick's Theorem   Game Theory       Green Hackenbush/Colon Principle/Fusion Principle       Nim       Sprague-Grundy Number   Matrix       Gaussian Elimination       Matrix Exponentiation   Data Structures       Basic Data Structures       Binary Indexed Tree       Binary Search Tree       Hashing       Orthogonal Range Search       Range Minimum Query/Lowest Common Ancestor       Segment Tree/Interval Tree       Trie Tree       Sorting       Disjoint Set   String       Aho Corasick       Knuth-Morris-Pratt       Suffix Array/Suffix Tree   Math       Basic Math       Big Integer Arithmetic       Number Theory           Chinese Remainder Theorem           Extended Euclid           Inclusion/Exclusion           Modular Arithmetic       Combinatorics           Group Theory/Burnside's lemma           Counting       Probability/Expected Value   Others       Tricky       Hardest       Unusual       Brute Force       Implementation       Constructive Algorithms       Two Pointer       Bitmask       Beginner       Discrete Logarithm/Shank's Baby-step Giant-step Algorithm       Greedy       Divide and Conquer   Dynamic Programming                   Tag it!

植物大战僵尸算个out的游戏了，原谅被出题逼疯了的跑来挖坟了。

会玩的请无视这一段直接看题目{

游戏中僵尸向你的房子进发，吃掉沿途遇到的植物进入你的房子 你就死翘了

你在土地上种植各种植物来攻击阻挡僵尸

手推车：放置在终点，僵尸走到面前会启动推倒一整行的僵尸

大蒜：可种植的一种植物，发出恶心的气味，僵尸咬了一口就会换到邻近的另一行（如果有相邻两行，那么移动到另外两行概率是相等的）

南瓜：单纯的肉盾 被僵尸啃的

耐久度K： 植物被咬了K口后被僵尸吃掉

如有其他对游戏的不理解请clarify

}

问题是这样的：

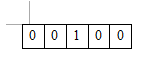
我们的院子变成了N行M列的，而且种满了大蒜（耐久度K）（图是我盗了 我不会这么无聊的）coming的僵尸只有一只（然而这只僵尸貌似发生了变异，它每啃一口植物，同一列相同种类的植物也被啃掉一口，一口一排的样子恩恩），初始位置在第S行，因为没有放置攻击性的植物，所以僵尸就一路吃了，于是出题者很想知道僵尸死在自上而下1-N号手推车的概率各是多少

（无视掉图中的南瓜，实际上对僵尸行走没有影响。。）

 

Input

一个整数T（表示T组数据）

接下来的T组数据

每组给定四个整数 N M K S

数据范围

T<=1000

0<N<=20

0<M<=1000

0<K<=1000

1<=S<=N

 

Output

对于每组数据输出一行N个4位小数 用空格隔开 表示僵尸死在相应行的概率 行末没有空格

 

Sample Input

1
5 9 5 3

Sample Output

0.0000 0.5000 0.0000 0.5000 0.0000

Source

第十一届北京师范大学程序设计竞赛决赛

 

 

解题思路：求出概率转移矩阵，因为要转移m*k次，即（原始概率矩阵B）*（概率转移矩阵A）^m*k，所以根据矩阵相乘的结合律，所以可以让概率转移矩阵A先乘m*k次，因为B矩阵为所以最后只需用B矩阵乘以转移矩阵，输出乘以后的矩阵的第一行。

 

 

 

#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
#include <vector>
#include <queue>
#include <set>
#include <map>
#include <math.h>
#include <string>
#include <stdlib.h>
#include <time.h>
using namespace std;
const int maxn = 1e5+300;
int n;
struct Matrix{
	double mat[25][25];
	Matrix(){
		for(int i = 1; i < 25; i++){
			for(int j = 1; j < 25; j++){
				mat[i][j] = 0.0;
			}
		}
	}
	void mem(){
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= n; j++){
				mat[i][j] = 0.0;
			}
		}
	}
	void unit(){
		for(int i = 1; i < 25; i++)
			mat[i][i] = 1.0;
	}
	Matrix operator *(const Matrix &rhs)const{
		Matrix ret;
		for(int i = 1; i <= n; i++){
			for(int j = 1; j <= n; j++){
				ret.mat[i][j] = 0.0;
				for(int k = 1; k <= n; k++){
					ret.mat[i][j] += mat[i][k]*rhs.mat[k][j];
				}

			}
		}
		return ret;
	}
};
void deg(const Matrix &rhs){
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= n; j++){
			printf("%.4lf ",rhs.mat[i][j]);
		}puts("");
	}
}

Matrix & Quick( Matrix &p, int k){
	Matrix ret;
	ret.unit();
	while( k ){
		if(k&1){
			ret = ret*p;
		}
		k >>= 1;
		p = p*p;
	}
	p = ret;
	return p;
} 
int main(){
	int T, m, k, s;
	scanf("%d",&T);
	while(T--){
		scanf("%d%d%d%d",&n,&m,&k,&s);
		Matrix ans, trans;
		ans.mem();
		trans.mem();
		for(int i = 1; i <= n; i++){
			if( i == 1 ){
				trans.mat[i][2] = 1.0;
			}else if( i == n ){
				trans.mat[i][n-1] = 1.0;
			}else{
				trans.mat[i][i-1] = 0.5;
				trans.mat[i][i+1] = 0.5;
			}
		}
		if(n == 1){
			puts("1.0000"); continue;
		}
		trans = Quick(trans,m*k);
//		deg(trans);
		ans.mat[1][s] = 1.0;
		ans = ans*trans;
		printf("%.4lf",ans.mat[1][1]);
		for(int i = 2; i <= n; i++)
			printf(" %.4lf",ans.mat[1][i]);
		puts("");
	}
}

　　

图文详解：

假设以n,m,k,s分别为5，9,9,3为例。P、PP、PPP分别代表咬1、2、3口后的概率，只是对于耐久度为9时，他们是在同一列的，只不过为了表示，所以这样给出，不要误解。PP₁=0*  P₁+0.5*  P₂+0*   P₃+0*  P₄+  0 * P₅

　　　　　　　　　　　　　　　　PP₂=1*  P₁+0 *    P₂+0.5*P₃+0*  P₄+0*    P₅

　　　　　　　　　　　　　　　　PP₃=0*  P₁+0.5*  P₂+0*   P₃+0.5*P₄+0*   P₅

　　　　　　　　　　　　　　　　PP₄=0*  P₁+0*    P₂+0.5* P₃+0*　P₄+1*   P₅

　　　　　　　　　　　　　　　　PP₅=0*  P₁+0*    P₂+0*    P₃+0.5*P₄+0*   P₅

由上表可以看出，后一个列概率矩阵PP由前一个概率矩阵P乘以某一个矩阵得到。我们假设该某矩阵为A即：

0	1	0	0	0
0.5	0	0.5	0	0
0	0.5	0	0.5	0
0	0	0.5	0	0.5
0	0	0	1	0

将列概率矩阵转为行概率矩阵B：

P1

P2

P3

P4

P5

用B*A得到下一个行概率矩阵B‘。同时由于矩相乘具有结合律，所以我们可以用矩阵快速幂来先求出转移m次的转移矩阵A^m*k，然后用原始矩阵B*A^m*k即可求得。