1.时域频域(详见:https://www.cnblogs.com/beipiaofeng/p/4325874.html)
https://blog.csdn.net/qq_33414271/article/details/79117586
1.时域频域的关系
时域分析与频域分析是对模拟信号的两个观察面。时域分析是以时间轴为坐标表示动态信号的关系;频域分析是把信号变为以频率轴为坐标表示出来。目前,信号分析的趋势是从时域向频域发展。时域故名思议就是随着时间的推移,我们所能直观感受的东西或事物,比如说音乐,我们听到动听的音乐,这是在时域上发生的事情。而对于演奏者来说音乐是一些固定的音符,我们听到的音乐在频域内是一个永恒的音符,音符的个数是有限且固定的,但可以组合出无限多的乐曲。
2.时域和频域的转换
动态信号从时间域变换到频率域主要通过傅立叶级数和傅立叶变换实现。周期信号靠傅立叶级数,非周期信号靠傅立叶变换。时域越宽,频域越短。

3.频域和时域:
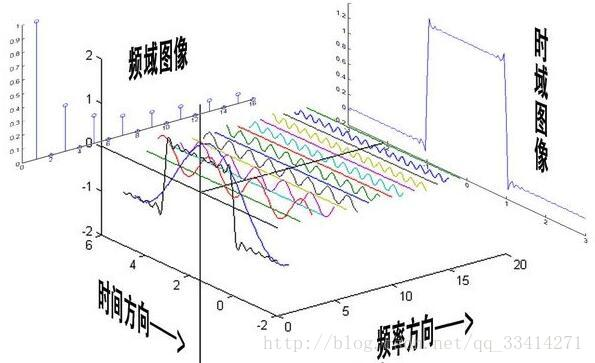
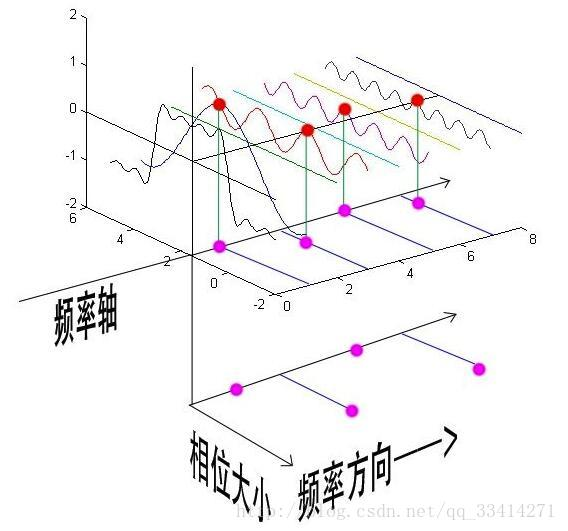
4. 相位谱
频谱只代表了一个正弦函数的幅值,而要准确描述一个正弦函数,我们不仅需要幅值,还需要相位,不同相位决定了波的位置,所以对于频域分析,仅仅有频谱(振幅谱)是不够的,我们还需要一个相位谱。
4.1.1 awgn(x, snr):函数awgn把加性高斯白噪声叠加到输入信息x中

clear all t=0:0.001:10; x=sin(2*pi*t); snr=20; y=awgn(x,snr); subplot(2,1,1);plot(t,x);title('正弦信号 x'); subplot(2,1,2);plot(t,y);title('添加了高斯白噪声后的正弦信号 x'); z=y-x; var(z)
4.1.2 awgn(s,snr,sigpower) 与1不同的是,加入了输入功率sigpower,单位:dBW
假设信号功率为10dBW,snr保持不变。

clear all t=0:0.001:10; x=sin(2*pi*t); snr=20; y=awgn(x,snr,10); %加入了输入功率sigpower subplot(2,1,1);plot(t,x);title('正弦信号 x'); subplot(2,1,2);plot(t,y);title('叠加了高斯白噪声后的正弦信号 x'); z=y-x; var(z)
4.1.3 awgn(x,snr,'measured') 首先输入信号x的功率,然后按照snr添加相应功率的高斯白噪声

clear all t=0:0.001:10; x=sin(2*pi*t); snr=20; awgn(x,snr,'measured') % subplot(2,1,1);plot(t,x);title('正弦信号 x'); subplot(2,1,2);plot(t,y);title('叠加了高斯白噪声后的正弦信号 x'); z=y-x; var(z)
