1 背景
后缀数组是处理字符串问题的有效算法,如最长公共字串,最长回文字串,重复次数最多的字串等等。所以学好它,对于以后处理处理字符串是很有帮助的。在网上找了下,发现对后缀数组讲的比较容易理解和清楚的是罗穗骞写的关于“后缀数组——处理字符串的有力工具”的论文,这篇文章主要总结下该论文中的主要内容。
2 定义
后缀:后缀是指从某个位置 i 开始到整个串末尾结束的一个特殊子串。字符串r 的从第 i 个字符开始的后缀表示为Suffix(i) , 也 就 是Suffix(i)=r[i..len(r)]。
后缀数组:后缀数组 SA 是一个一维数组,它保存 1..n 的某个排列 SA[1],SA[2],......,SA[n],并且保证 Suffix(SA[i]) < Suffix(SA[i+1]),1≤i<n。也就是将 S 的 n 个后缀的后缀从小到大进行排序之后把排好序的开头位置顺次放入 SA 中。
名次数组:名次数组 Rank[i]保存的是 Suffix(i)在所有后缀中从小到大排列的“名次”。
height 数组:定义 height[i]=suffix(sa[i-1])和 suffix(sa[i])的最长公共前缀,也就是排名相邻的两个后缀的最长公共前缀。
3 性质
(a)后缀数组和名次数组为互逆运算,后缀数组表示排名第几的是谁,名次数组表示谁排名第几,即sa[rank[i]] = i, rank[sa[i]] = i。
(b)定 义h[i]=height[rank[i]],也就是 suffix(i)和在它前一名的后缀的最长公共前缀。h[i]有如下性质:
h[i]≥h[i-1]-1
证明:设 suffix(k)是排在 suffix(i-1)前一名的后缀,则它们的最长公共前缀是h[i-1]。那么 suffix(k+1)将排在 suffix(i)的前面(这里要求 h[i-1]>1,如果h[i-1]≤1,原式显然成立)并且 suffix(k+1)和 suffix(i)的最长公共前缀是h[i-1]-1,所以 suffix(i)和在它前一名的后缀的最长公共前缀至少是 h[i-1]-1。
4 实现
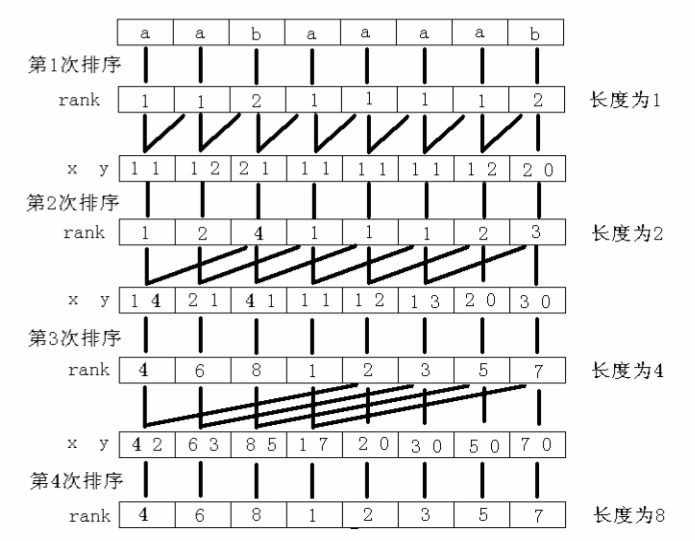
求解后缀数组和名次数组:用倍增的方法对每个字符开始的长度为 2k 的子字符串进行排序,求出排名,即 rank 值。k 从 0 开始,每次加 1,当 2k 大于 n 以后,每个字符开始的长度为 2k 的子字符串便相当于所有的后缀。并且这些子字符串都一定已经比较出大小,即 rank 值中没有相同的值,那么此时的 rank 值就是最后的结果。每一次排序都利用上次长度为 2k-1 的字符串的 rank 值,那么长度为 2k 的字符串就可以用两个长度为 2k-1 的字符串的排名作为关键字表示,然后进行基数排序,便得出了长度为 2k 的字符串的 rank 值。以字符串“aabaaaab”为例,整个过程如下图所示。其中 x、y 是表示长度为 2k 的字符串的两个关键字 。
 计算数组height:可以令i从0到n-1依次求出h[i]。初始化k = 0,k表示h[i]的值。具体分下面两种情况
计算数组height:可以令i从0到n-1依次求出h[i]。初始化k = 0,k表示h[i]的值。具体分下面两种情况
(1)如果rank[i] == 0,说明suffix(i)排名第一,则h[i] = 0,此时k也更新为0。
(2)如果rank[i] > 0, 求出排在suffix(i)前一名的下标为j = sa[rank[i] - 1]。而此时的k表示的是h[i - 1]的值,根据前面的性质b,当前的h[i] >= h[i - 1] - 1,即h[i] >= k - 1。为了确定当前的h[i],则只需要从suffix(i)和suffix(j)的第k位开始比较(通过h[i],省去了前面的k-1次比较,类似与dp的思想)来确定h[i]。
具体实现:
1 #include <stdio.h>
2 #include <string.h>
3
4 #define MAXSIZE 400005
5 #define min(a, b) a < b ? a : b
6 int sa[MAXSIZE], rank[MAXSIZE], height[MAXSIZE],temp[MAXSIZE];
7
8 int cmp(int *r, int a, int b, int l)
9 {
10 return (r[a] == r[b] && r[a + l] == r[b + l]);
11 }
12
13 int get_suffix(char *str, int n)
14 {
15 int *t, *x = rank, *y = temp, ws[MAXSIZE], wv[MAXSIZE], i, j, k, m;
16
17 //对字符串中的字符进行基数排序
18 m = 128;
19 for (i = 0; i < m; i++)
20 ws[i] = 0;
21 for (i = 0; i < n; i ++)
22 ws[x[i] = str[i]]++;
23 for (i = 1; i < m; i ++)
24 ws[i] += ws[i - 1];
25 for (i = n - 1; i >= 0; i--)
26 sa[--ws[x[i]]] = i;
27
28 for (j = 1, k = 1; k < n; j *= 2)
29 {
30 //对第二关键字排序
31 k = 0;
32 for (i = n - j; i < n; i++)
33 y[k++] = i;
34 for (i = 0; i < n; i ++)
35 if (sa[i] >= j)
36 y[k++] = sa[i] - j;
37 //对第一关键字排序
38 for (i = 0; i < n; i ++)
39 wv[i] = x[y[i]];
40 for (i = 0; i < m; i ++)
41 ws[i] = 0;
42 for (i = 0; i < n; i ++)
43 ws[wv[i]]++;
44 for (i = 1; i < m; i ++)
45 ws[i] += ws[i - 1];
46 for (i = n - 1; i >= 0; i --)
47 sa[--ws[wv[i]]] = y[i];
48 //对x数组进行修正
49 for (t = y, y = x, x = t, k = 1, x[sa[0]] = 0, i = 1; i < n; i ++)
50 x[sa[i]] = cmp(y, sa[i], sa[i - 1], j) ? k - 1 : k++;
51 m = k;
52 }
53 //计算rank
54 for (i = 0; i < n; i ++)
55 rank[sa[i]] = i;
56 //计算height
57 k = 0;
58 for (i = 0; i < n; i ++)
59 {
60 if (rank[i] == 0)
61 {
62 height[0] = k = 0;
63 continue;
64 }
65 if (k > 0)
66 k--;
67 j = sa[rank[i] - 1];
68 while (j + k < n && i + k < n && str[j + k] == str[i + k])
69 k++;
70 height[rank[i]] = k;
71 }
72 }
参考:后缀数组——处理字符串的有力工具 罗穗骞