一般的素数筛选的思路是从2开始,将所有2的倍数去掉,然后从3开始,将3的倍数去掉,然后从下一个素数x开始,将x的倍数去掉...,这样可以将所有素数的倍数去掉。实现代码如下:
1 int PrimeOld() 2 { 3 int i; 4 5 cnt = 0; 6 memset(prime, true, sizeof(prime)); 7 for (i = 2; i < MAX; i++) 8 { 9 if (prime[i]) 10 { 11 primeUse[cnt++] = i; 12 for (int j = i + i; j < MAX; j += i) 13 { 14 prime[j] = false; 15 allCount++; 16 } 17 } 18 } 19 }
从上面的代码不难看出,还是会存在重复访问的情况,如i = 2和 i = 5的情况都会访问prime[20]。因此改进这个算法的方法就是尽量重复访问的次数,尽量让prime[j]只能被访问一次。上面代码的思路是素数的倍数一定不是素数,那么任何一个数与素数的乘积肯定也不是素数,基于这个思想的代码如下:
1 int PrimeNew() 2 { 3 int i; 4 5 memset(prime, true, sizeof(prime)); 6 allCount = 0; 7 cnt = 0; 8 for (i = 2; i < MAX; i++) 9 { 10 if (prime[i]) 11 primeUse[cnt++] = i; 12 for (int j = 0; j < cnt && i * primeUse[j] < MAX; j++) 13 { 14 prime[i * primeUse[j]] = false; 15 allCount++; 16 if (i % primeUse[j] == 0) 17 break; 18 } 19 } 20 }
上面代码和前面最大代码的不同是产生剔除整数的方法不同,前者是根据当前处理到的素数的倍数来剔除,后者则是根据当前整数与已经产生的素数的乘积来剔除,效果是一样的。但后者有一个关键的优化就是当当前处理的整数已经是某个素数的倍数时,退出剔除。如果没有这个优化,那么还是有些prime[j]被重复访问了,如prime[12],它显示通过prime[6 * 2]被访问,然后通过prime[4 * 3]被访问。我们应该让12只被12的最小素因子2访问,即计算6 * 2时访问,而不应该在4 * 3时访问,所有对于任何数如果它是当前素数的倍数那么它就不能再与素数表中该素数之后的素数相乘了。
测试结果也可以看出后一种方法能够很有效的减少对同一个prime[j]的访问。
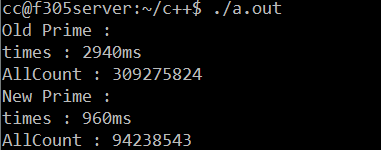
上面的测试结果是通过对1~100000000之间的素数筛选。times表示的是筛选所用的时间,AllCount表示再第二重循环中访问prime数组的总次数。可以很明显的看出,改进的方法在时间上有了比较大的提升。测试的源代码:https://github.com/cc1989/test/blob/master/primes.cpp
参考:http://blog.csdn.net/morewindows/article/details/7347459