题目描述:小度和小良最近又迷上了下棋。棋盘一共有N行M列,我们可以把左上角的格子定为(1,1),右下角的格子定为(N,M)。在他们的规则中,“王”在棋盘上的走法遵循十字路线。也就是说,如果“王”当前在(x,y)点,小度在下一步可以移动到(x+1, y), (x-1, y), (x, y+1), (x, y-1), (x+2, y), (x-2, y), (x, y+2), (x, y-2) 这八个点中的任意一个。
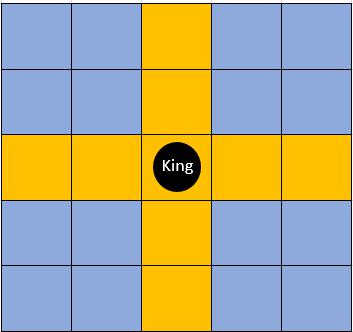
小度觉得每次都是小良赢,没意思。为了难倒小良,他想出了这样一个问题:如果一开始“王”在(x0,y0)点,小良对“王”连续移动恰好K步,一共可以有多少种不同的移动方案?两种方案相同,当且仅当它们的K次移动全部都是一样的。也就是说,先向左再向右移动,和先向右再向左移动被认为是不同的方案。
输入:输入包括多组数据。输入数据的第一行是一个整数T(T≤10),表示测试数据的组数。每组测试数据只包括一行,为五个整数N,M,K,x0,y0。(1≤N,M,K≤1000,1≤x0≤N,1≤y0≤M)
输出:对于第k组数据,第一行输出Case #k:,第二行输出所求的方案数。由于答案可能非常大,你只需要输出结果对9999991取模之后的值即可。
这个题目,开始做的时候挺纠结,最直接的思路就是从王的起始点一步一步的计算到达其它位置的方案数,不过复杂度太高,会超时,下面先说下自己开始的思路,然后通过这个思路改进来解决这道题目。定义一个数组dp[x][i][j](0<=x<=k,1<=i<=n,1<=j<=m),表示经过x步到达位置(i,j)的方案数,move[8][2] = {{1,0},{-1,0},{0,1},{0,-1},{2,0},{-2,0},{0,2},{0,-2}},那么dp[x+1][i][j] = sumo(dp[x][i - move[o][0]][j - move[o][1]])(0<=o<8),sumo表示以o变化来累加,最终只要将dp[k][i][j](1<=i<=n,1<=j<=m)都加就是总的方案数了。但由于k,n,m的最大值都为1000,所以直接定义dp[1001][1001][1001]占用的存储空间过大,再看前面的推导式子dp[x+1][i][j]只与dp[x][i'][j']有关,所以可以定义滚动数组dp[2][1001][1001]来节约空间。可以很容易的看出这个思路的复杂度是O(k*n*m),显然这个复杂度不能满足题目要求。
可不可以根据上面思路优化下呢,最终我们需要计算dp[k][i][j](1<=i<=n,1<=j<=m)的和,前面的思路是一步一步经过k步来推导出dp[k][i][j],可以不可以用起来的方法求dp[k][i][j]呢?考虑到这是一个矩阵,移动的方向只能是行或者列,所有很自然想到行列步数的组合来求dp[k][i][j],即dp[k][i][j] = sumt(C[k][t] * dp1[t][i] * dp2[k - t][j]),dp1[t][i]表示在列方向经过t步到达i,dp2[k - t][j]表示在行方向经过k - t步到达j,C[k][t]是组合数。计算dp1和dp2可以通过前面一步一步推的思路求解,只是维度变成一维的了,复杂度分别为O(k * n), O(k * m)。求最终结果也是将所有dp[k][i][j](1<=i<=n,1<=j<=m)加起来,这个计算式和前面不同的是由于行列式独立的,所以最终的ans = sumi(sumj(sumt(C[k][t] * dp1[t][i] * dp2[k - t][j]))) = sumt(C[k][t] * sumi(dp1[t][i]) * sumj(dp2[k - t][j])),C[k][t]可以根据组合数的性质C[k][t] = C[k - 1][t] + C[k - 1][t - 1]求得,所以这个思路的算法复杂度为O(max( k * n, k * m, k^2)),可以满足题目要求了。
具体代码如下:
1 #include <iostream> 2 #include <cstring> 3 using namespace std; 4 5 int n, m, k, x0, y0; 6 long long dp1[1001][1001], dp2[1001][1001], c[1001][1001]; 7 int move[4] = {1, -1, 2, -2}; 8 9 void dp(long long dp[][1001], int start, int end, int x) 10 { 11 dp[0][x] = 1; 12 for (int i = 0; i < k; i++) 13 { 14 for (int j = start; j <= end; j++) 15 if (dp[i][j]) 16 { 17 for (int k = 0; k < 4; k++) 18 { 19 int ii = j + move[k]; 20 if (ii >= start && ii <= end) 21 dp[i + 1][ii] = (dp[i + 1][ii] + dp[i][j]) % 9999991; 22 } 23 } 24 } 25 } 26 void pl() 27 { 28 for (int i = 0; i < 1001; i++) 29 c[i][0] = 1; 30 for (int i = 1; i < 1001; i++) 31 for (int j = 1; j <= i ; j++) 32 c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % 9999991; 33 } 34 35 int main() 36 { 37 int t; 38 int ans; 39 pl(); 40 cin >> t; 41 for (int i = 1; i <= t; i++) 42 { 43 cin >> n >> m >> k >> x0 >> y0; 44 45 memset(dp1, 0, sizeof(dp1)); 46 memset(dp2, 0, sizeof(dp2)); 47 dp(dp1, 1, n, x0); 48 dp(dp2, 1, m, y0); 49 ans = 0; 50 for (int j = 0; j <= k; j++) 51 { 52 for (int ii = 1; ii <= n; ii++) 53 dp1[j][0] = (dp1[j][0] + dp1[j][ii]) % 9999991; 54 for (int ii = 1; ii <= m; ii++) 55 dp2[j][0] = (dp2[j][0] + dp2[j][ii] ) % 9999991; 56 } 57 for (int j = 0; j <= k; j++) 58 ans = (ans + (((c[k][j] * dp1[j][0]) % 9999991) * dp2[k - j][0]) % 9999991) % 9999991; 59 cout << "Case #" << i << ":" << endl << ans << endl; 60 } 61 return 0; 62 }