Lucas 定理(证明)
A、B是非负整数,p是质数。AB写成p进制:A=a[n]a[n-1]...a[0],B=b[n]b[n-1]...b[0]。
则组合数C(A,B)与C(a[n],b[n])*C(a[n-1],b[n-1])*...*C(a[0],b[0]) mod p 相同
即:Lucas(n,m,p)=c(n%p,m%p)*Lucas(n/p,m/p,p)
证明:
首先我们注意到 n=(ak...a2,a1,a0)p = (ak...a2,a1)p * p + a0
= [n/p]*p+a0
且m=[m/p]+b0
只要我们更够证明 C(n,m)=C([n/p],[m/p]) * C(a0,b0) (mod p)
剩下的工作由归纳法即可完成
我们知道对任意质数p: (1+x)^p == 1+(x^p) (mod p)
注意!这里一定要是质数。
(为什么要是质数呢?
因为(1+x)^p=1^p+c(p,1)x+c(p,2)x^2+...+x^p
但p为质数时c(p,1),c(p,2),...,c(p,p-1) 模p都为0
所以(1+x)^p == 1+x^p (mod p)
)
对 模p 而言,接下来是让我惊叹的一个构造证明,证明只有一个公式如下:
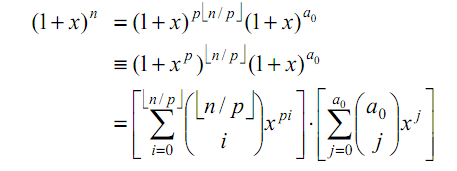
上式左右两边的x^m的系数对模p而言一定同余(为什么),其中左边的x^m的系数是 C(n,m) 而由于a0和b0都小于p
右边的x^m ( = x^(([m/p]*p)+b0)) 一定是由 x^([m/p]*p) 和 x^b0 相乘而得 (即发生于 i=[m/p] , j=b0 时) 因此我们就有了
C(n,m)=C([n/p],[m/p]) * C(a0,b0) (mod p)
perfect!