POJ 2553 The Bottom of a Graph

Description

We will use the following (standard) definitions from graph theory. Let V be a nonempty and finite set, its elements being called vertices (or nodes). Let E be a subset of the Cartesian product V×V, its elements being called edges. Then G=(V,E) is called a directed graph.
Let n be a positive integer, and let p=(e₁,...,e_n) be a sequence of length n of edges e_i∈E such that e_i=(v_i,v_i+1) for a sequence of vertices (v₁,...,v_n+1). Then p is called a path from vertex v₁ to vertex v_n+1 in G and we say that v_n+1 is reachable from v₁, writing (v₁→v_n+1).
Here are some new definitions. A node v in a graph G=(V,E) is called a sink, if for every node w in G that is reachable from v, v is also reachable from w. The bottom of a graph is the subset of all nodes that are sinks, i.e., bottom(G)={v∈V|∀w∈V:(v→w)⇒(w→v)}. You have to calculate the bottom of certain graphs.

Input

The input contains several test cases, each of which corresponds to a directed graph G. Each test case starts with an integer number v, denoting the number of vertices of G=(V,E), where the vertices will be identified by the integer numbers in the set V={1,...,v}. You may assume that 1<=v<=5000. That is followed by a non-negative integer e and, thereafter, e pairs of vertex identifiers v₁,w₁,...,v_e,w_e with the meaning that (v_i,w_i)∈E. There are no edges other than specified by these pairs. The last test case is followed by a zero.

Output

For each test case output the bottom of the specified graph on a single line. To this end, print the numbers of all nodes that are sinks in sorted order separated by a single space character. If the bottom is empty, print an empty line.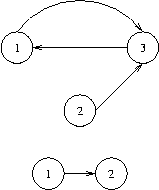

Sample Input

3 3
1 3 2 3 3 1
2 1
1 2
0

Sample Output

1 3
2

Source

Ulm Local 2003

 

 

题意：求没有出度的强连通分量的点。

 

#include <stdio.h>
#include <string.h>
#define MAXN 5001

int m;
int cnt;
struct node{
    int to,next;
}edge[MAXN*MAXN];

int temp[MAXN];
int head[MAXN];
int dfn[MAXN];
int low[MAXN];
int sta[MAXN];
int flag[MAXN];

void addedge(int u, int v){
    edge[cnt].to=v;
    edge[cnt].next=head[u];
    head[u]=cnt++;
}

int min(int a, int b){
    if(a<b)return a;
    else return b;
}

int tarbfs(int k ,int lay, int& scc_num){
    temp[k]=1;
    low[k]=lay;
    dfn[k]=lay;
    sta[++m]=k;
    for(int i=head[k]; i!=-1; i=edge[i].next){
        if(temp[edge[i].to]==0){
            tarbfs(edge[i].to,++lay,scc_num);
        }
        if(temp[edge[i].to]==1)low[k]=min(low[k],low[edge[i].to]);
    }
    if(dfn[k]==low[k]){
        ++scc_num;
        do{
            low[sta[m]]=scc_num;
            temp[sta[m]]=2;
        }while(sta[m--]!=k);
    }
    return 0;
}

int tarjan(int n){
    int scc_num=0;
    int lay=1;
    m=0;
    memset(temp,0,sizeof(temp));
    memset(low,0,sizeof(low));
    for(int i=1; i<=n; i++){
        if(temp[i]==0)tarbfs(i,lay,scc_num);
    }
    return scc_num;
}

int main(int argc, char *argv[])
{
    int n,t,v,u;
    cnt=0;
    while(scanf("%d",&n),n){
        scanf("%d",&t);
        memset(head,-1,sizeof(head));
        memset(flag,0,sizeof(flag));
        for(int i=0; i<t; i++){
            scanf("%d %d",&v,&u);
            addedge(v,u);
        }
        tarjan(n);
        for(int i=1; i<=n; i++){
            for(int j=head[i]; j!=-1; j=edge[j].next){
                if(low[edge[j].to]!=low[i]){
                    flag[low[i]]=1;
                    break;
                }
            }
        }
        for(int i=1; i<=n; i++){
            if(!flag[low[i]]){
                if(i!=n){
                    printf("%d ",i);
                }else{
                    printf("%d",i);
                }
            }
        }
        printf("
");
    }
    return 0;
}